Название: Зависимость дальности перелета объекта от угла бросания
Вид работы: контрольная работа
Рубрика: Авиация и космонавтика
Размер файла: 107.46 Kb
Скачать файл: referat.me-127.docx
Краткое описание работы: Движения тел в сферически симметричном гравитационном поле. Решение баллистической задачи, на нахождение начальной скорости и начального угла бросания тела, при которых обеспечивается перелет тела, на заданное расстояние с наименьшими энергозатратами.
Зависимость дальности перелета объекта от угла бросания
Вступление:
При движении тел в однородном гравитационном поле, их траектории представляют собой параболы. И решая задачу относительно дальности полета, как функции начальной скорости и угла бросания тела, можно найти максимальную дальность перелета:
![]() ,
, ![]()
А, следовательно, и обратное решение для начальных, угла и скорости бросания тела, при которых обеспечивается перелет на заданное, максимальное расстояние.
![]() ,
, ![]() ,
,
Угол ![]() отсчитывается от горизонта.
отсчитывается от горизонта.
При рассмотрении движения тел в сферически симметричном гравитационном поле, их траектории, представляют собой эллипсы, в одном из фокусов которых, находится источник гравитационного поля (в случае сферически симметричных тел - центр притягивающего центрального тела). Если бросание тел производить с поверхности центрального тела (Планеты), то дальность перелета (т.е. расстояние от точки бросания до точки падения) можно представить в виде длины дуги на поверхности сферы. Тогда, решая баллистическую задачу, можно найти такие начальную скорость и начальный угол бросания тела, при которых обеспечивается перелет тела, на заданное расстояние с наименьшими энергозатратами.
Решение:
Для решения данной задачи в первую очередь найдем функцию дальности перелета брошенного тела от начальной скорости и начального угла бросания. А так же всесторонне изучим данную зависимость.
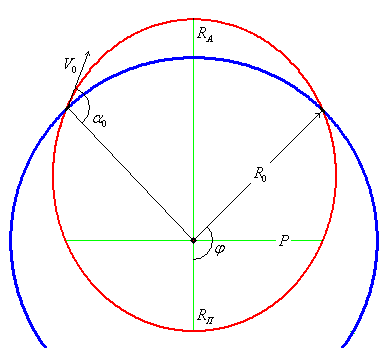
![]() -Радиус планеты
-Радиус планеты
![]() -Начальная скорость
-Начальная скорость
![]() -Начальный угол
-Начальный угол
![]() -Параметр орбиты
-Параметр орбиты
![]() -Гравитационный параметр планеты
-Гравитационный параметр планеты
![]() -Дальность бросания тела
-Дальность бросания тела ![]()
Как видно из рисунка, для нахождения ![]() , необходимо найти угол
, необходимо найти угол ![]() . Применяя результаты решения задачи Кеплера и используя не сложные вычисления, найдем зависимость
. Применяя результаты решения задачи Кеплера и используя не сложные вычисления, найдем зависимость
![]() .
.
Т.к. ![]()
(Где ![]() - эксцентриситет орбиты)
- эксцентриситет орбиты)
То, выражая значения параметра и эксцентриситета орбиты через ![]() и
и ![]() , получим конечное выражение:
, получим конечное выражение:
Для простоты обозначим:
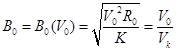 , т.к.
, т.к.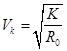 .
.
В результате будем иметь:
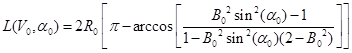
Итак, мы получили зависимость дальности перелета брошенного тела от начальных скорости и угла бросания. Так как при незначительных скоростях бросания и дальность перелета брошенного тела также будет незначительна, а в качестве траектории брошенного тела будет выступать апоцентрическая окрестность эллипса, которая аппроксимируется (приближается) параболой, то можно ожидать, что при небольшой скорости (скоростях, много меньших первой космической скорости) бросания, максимальная дальность будет обеспечиваться при угле бросания, близкому к значению ![]() от горизонта, т.е. при
от горизонта, т.е. при ![]() .
.
Действительно, изобразив графически зависимость дальности бросания тела [Km] от угла вектора скорости к горизонту, (при фиксированной скорости) можно проследить данный факт.
B=0.1
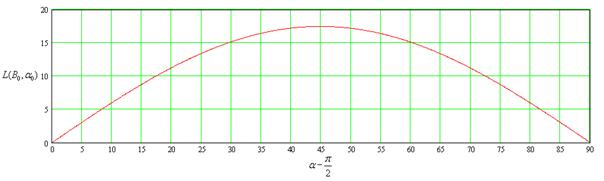
B=0.6
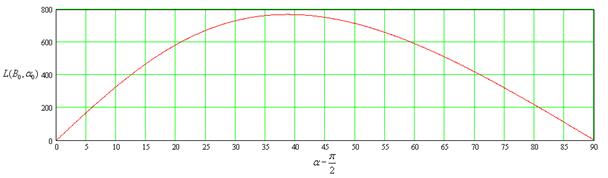
B=0.9
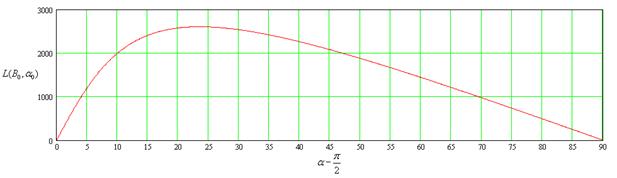
Из графиков видно, что при незначительных скоростях бросания, максимум зависимости приходится на угол равный 45 градусов от горизонта. А при дальнейшем увеличении скоростей, максимум дальности перелета смещается в сторону малых углов. И при приближении скорости бросания к круговой скорости (первой космической), выше приведенная зависимость переходит в прямую, имеющую максимальное значение при 0 градусов, равное ![]() , т.е. половину длины окружности планеты.
, т.е. половину длины окружности планеты.
B=1.0
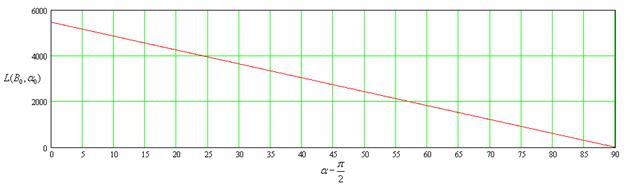
То есть мы увидели, что максимальная дальность перелета тела, при фиксированной скорости бросания, обеспечивается при определенном угле, который является функцией скорости броска. Чтобы найти данный угол, продифференцируем функцию дальности броска по углу бросания и после чего, приравняв ее к нулю, выразим значение угла.
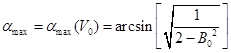
А после подстановки данного выражения обратно в зависимость дальности, найдем максимальное расстояние броска, которое можно обеспечить при заданной начальной скорости ![]() . Т.е. т.к.
. Т.е. т.к.
![]() , определим максимально возможную дальность перелета, как функцию начальной скорости.
, определим максимально возможную дальность перелета, как функцию начальной скорости.
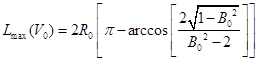
Решая обратную задачу, можно зная расстояние, на которое необходимо бросить тело, найти ту оптимальную скорость и угол броска, при которых обеспечится перелет тела на данное расстояние с наименьшими энергозатратами.
Для решения данной задачи, составим квадратное уравнение для выражения ![]() . Где обозначим:
. Где обозначим: 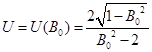 . С учетом данных замен, уравнение примет вид:
. С учетом данных замен, уравнение примет вид:
![]()
Чтобы оценить корни уравнения, построим графики для ![]() при различных значениях
при различных значениях ![]() .
.
Так как ![]() ,
, ![]()
![]() .
.
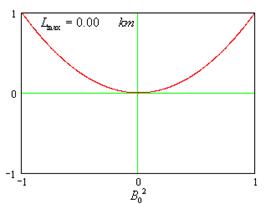
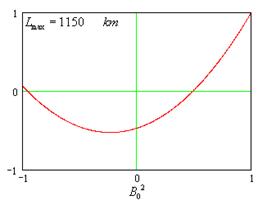
Из графиков квадратного уравнения можно заметить, что при малых дальностях броска, два корня данного уравнения практически совпадают в окрестности![]() , но при увеличении дальности броска до значения
, но при увеличении дальности броска до значения ![]() решение распадается на две части. Причем один корень всегда положительный, а другой отрицательный. А так как
решение распадается на две части. Причем один корень всегда положительный, а другой отрицательный. А так как ![]() , отрицательный корень отбрасываем, так как он не имеет смысла.
, отрицательный корень отбрасываем, так как он не имеет смысла.
И находя положительное решение данного уравнения, имеем:
![]()
Откуда легко получить значение скорости, при которой обеспечивается перелет на заданное расстояние (по оптимальной траектории).
Т.к. ![]() , то получим конечное выражение:
, то получим конечное выражение:
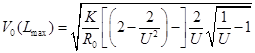
А, подставляя данное выражение в формулу для оптимального угла, найдем значение угла, при котором обеспечивается перелет.
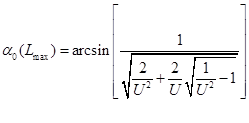
Итак, задача решена!!!
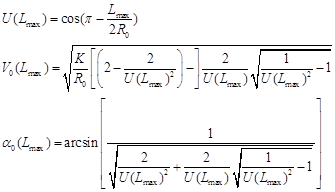
Все графики построены на примере бросания тел с Лунной поверхности:
![]() ,
, ![]()
Примечания:
1. Апоцентр - наиболее удаленная от центрального тела точка эллиптической орбиты.
2. Апоцентрическая окрестность- окрестность эллипса, в близи точки апоцентра.
3. ![]() - гравитационный параметр планеты, где
- гравитационный параметр планеты, где ![]() - гравитационная постоянная,
- гравитационная постоянная, ![]() - масса планеты. Используется в качестве упрощения записи выражений, а также по причине того, что гравитационный параметр планет гораздо более точно определен из эксперимента, нежели определены гравитационная постоянная и массы планет в отдельности.
- масса планеты. Используется в качестве упрощения записи выражений, а также по причине того, что гравитационный параметр планет гораздо более точно определен из эксперимента, нежели определены гравитационная постоянная и массы планет в отдельности.
4. Понятие эксцентриситета орбиты вводится в аналитической геометрии при изучении кривых второго порядка (конических сечений). Эксцентриситет характеризует степень вытянутости орбиты (эллипса), и для замкнутых орбит лежит в интервале от 0 до 1. Т.е. для абсолютно круглой орбиты эксцентриситет равен 0, для параболической орбиты его значение равно 1, для гиперболических траекторий значение эксцентриситета больше 1.
В случае замкнутых орбит:
![]() , где
, где ![]() - расстояние от центра эллипса до одного из его фокусов,
- расстояние от центра эллипса до одного из его фокусов, ![]() - большая полуось орбиты (эллипса.)
- большая полуось орбиты (эллипса.)
5. ![]() и
и ![]() - некоторые функции, которые используются тля упрощения записи выражений. Т.е. на самом деле
- некоторые функции, которые используются тля упрощения записи выражений. Т.е. на самом деле ![]() имеет довольно громоздкий вид, и целесообразно в данной зависимости сделать замену
имеет довольно громоздкий вид, и целесообразно в данной зависимости сделать замену 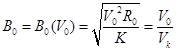 . К тому же данная замена позволит более наглядно оценить вышеприведенную зависимость. В данном случае
. К тому же данная замена позволит более наглядно оценить вышеприведенную зависимость. В данном случае ![]() - это отношение скорости бросания, к первой космической скорости. Аналогичным образом и для подобных целей производится замена
- это отношение скорости бросания, к первой космической скорости. Аналогичным образом и для подобных целей производится замена 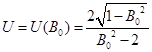 .
.
Похожие работы
-
Звездная аберрация против релятивистской астрономии
Новая интерпретация преобразования Лоренца. Преобразование Лоренца, сохраняющее уравнения Максвелла инвариантными, имеет дело с действительным объектом и его положением в пространстве и с мнимым отображением этого объекта в пространстве световыми лучами.
-
Пространственно-временная метрика, уравнения геодезических. Ньютоново приближение
В соответствии с теорией относительности метрика зависит от распределения материи. Анализ статического сферически симметричного поля, создаваемого изолированной массой. Определение евклидова пространства тремя взаимно ортогональными декартовыми осями.
-
Особенности гравитационного взаимодействия
Сущность гравитации и история развития теории, ее обосновывающей. Законы движения планет (в том числе Земли) вокруг Солнца. Природа гравитационных сил, значение в развитии знаний о них теории относительности. Особенности гравитационного взаимодействия.
-
Как обнаружить "черную дыру"
Свойства "черной дыры" - пространства, в которой гравитационное притяжение настолько сильно, что ни вещество, ни излучение не могут эту область покинуть. Косвенные признаки нахождения "черной дыры", искажение нормальных характеристик ближайших объектов.
-
Су-30мки, общие сведения
12.02.02.159.№9.Р ИАТ Су-30мки Тема: Общие сведения Преподаватель: Студент: Миронов А.А. Давидович А.А. Дата: Дата: Подпись: Подпись: 2003 Двухместный сверхзвуковой многофункциональный истребитель СУ-30МКИ, созданный совместными усилиями специалистов ОКБ им. П.О. Сухого и Иркутского авиационного производственного объединения – первый отечественный самолет, разработанный специально под требования зарубежного заказчика, стратегического союзника России – Индии.
-
Применение фильтра Калмана в задаче идентификации отказов двигателей стабилизации космического аппарата
УДК 629.195 Ю.А. КУЗНЕЦОВ, канд. техн. наук, АО “Хартрон” Е.В. УХАНОВ, студент НТУ “ХПИ” ПРИМЕНЕНИЕ ФИЛЬТРА КАЛМАНА В ЗАДАЧЕ ИДЕНТИФИКАЦИИ ОТКАЗОВ ДВИГАТЕЛЕЙ СТАБИЛИЗАЦИИ КОСМИЧЕСКОГО АППАРАТА
-
Системы небесных координат
Географическая система координат. Горизонтальная система координат. Экваториальные системы координат. Эклиптическая система координат. Галактическая система координат. Системы счёта времени. Звёздное время. Переход от одной системы координат к другой.
-
Система небесных координат
Горизонтальная система небесных координат. Экваториальная система небесных координат. Эклиптическая система небесных координат. Галактическая система небесных координат. Изменение координат при вращении небесной сферы. Использование различных систем коорд
-
Проектирование твердотопливного ракетного двигателя третьей ступени трехступенчатой баллистической ракеты
Выбор основных параметров ракетных двигателей на твердом топливе (РДТТ). Расчет теплозащитного покрытия двигателя. Выбор давления в камере сгорания и на срезе сопла. Расчет характеристик прогрессивности щелевого заряда и звездчатого заряда РДТТ.
-
Анализ и расчет характеристик среднеорбитальной системы типа: ГЛОНАС, NAV-STAR
Анализ орбит и движения искусственных спутников Земли (ИСЗ). Принципы работы и формирования излучаемых сигналов аппаратуры ИСЗ, применительно среднеорбитальной системы типа: ГЛОНАС, NAV-STAR. Основные понятия пространственной угловой ориентации судна.