Название: Дисперсность

Вид работы: реферат

Рубрика: Химия

Размер файла: 56.99 Kb

Скачать файл: referat.me-370410.docx

Краткое описание работы: Понятие и суть дисперсности, ее характеристика. Шкала дисперсности. Удельная поверхность и ее степень дисперсности. Классификация дисперсных систем. Понятия: дисперсная фаза и дисперсионная среда. Методы получения дисперсных систем и их особенности.

Дисперсность

Шкала дисперсности.

Удельная поверхность. Степень дисперсности. Классификация

дисперсных систем. Понятия: дисперсная фаза и дисперсионная

среда. Методы получения дисперсных систем

Дисперсной называют систему, в которой одно вещество распределено в среде другого, причем между частицами и дисперсионной средой есть граница раздела фаз. Дисперсные системы состоят из дисперсной фазы и дисперсионной среды.

Дисперсная фаза - это частицы, распределенные в среде. Ее признаки: дисперсность и прерывистость (рис. 1.1.1.1).

Дисперсионная среда - материальная среда, в которой находится дисперсная фаза. Ее признак - непрерывность .

Поверхность раздела фаз характеризуется раздробленностью и гетерогенностью. Раздробленность характеризуется:

1) степенью дисперсности : , [см^-1 ; м^-1 ], где S - суммарная межфазная поверхность или поверхность всех частиц дисперсной фазы; V - объем частиц дисперсной фазы.

2) дисперсностью - величиной, обратной минимальному размеру:

[; ];

3)удельной поверхностью : , [м² /кг; см² /г]; где m - масса частиц дисперсной фазы.

4) кривизной поверхности : . Для частицы неправильной формы ,

где r ₁ и r ₂ - радиусы окружностей при прохождении через поверхность и нормаль к ней в данной точке двух перпендикулярных плоскостей.

5) размером тела по трем осям , причем определяющим является размер по той оси, где он минимальный. В зависимости от размеров частиц они имеют свои исторические названия (см. рис. 1.1.1.1).

Классификация дисперсных систем осуществляется по нескольким признакам (рис. 1.1.1.2).

1. По дисперсности различают:

а) грубодисперсные системы, для них D < 10³ [1/см] (рис. 1.1.1.3);

б) микрогетерогенные системы, для них D = 10³ - 10⁵ [1/см];

в) ультрамикрогетерогенные системы, для них D = 10⁵ - 10⁷ [1/см].

2. По агрегатному состоянию дисперсной фазы и дисперсионной среды. Эта классификация была предложена Оствальдом (см. табл. 1.1.1.1).

3. По структуре дисперсные системы различают:

1) свободные дисперсные системы, когда частицы обеих составляющих системы могут свободно перемещаться друг относительно друга (золь);

2) связанные дисперсные системы, когда одна из составляющих системы представляет собой структурированную систему, т.е. частицы фазы жестко связаны между собой (студень, композиты).

Таблица 1.1.1.1

Классификация по агрегатному состоянию фаз

Агрегатное состояние дисперсной фазы	Агрегатное состояние дисперсион-ной среды	Условное обозначение фаза/среда	Название системы	Примеры
г	г	г/г ж/г тв/г	Аэрозоли	атмосфера Земли
ж	г			туман, слоистые облака
тв	г			дымы, пыли, перистые облака
г	ж	г/ж	Газовые эму-льсии, пены	газированная вода, мыльная и пивная пены
ж	ж	ж/ж	Эмульсии	молоко, масло сливочное, кремы и т.д.
тв	ж	тв/ж	Лиозоли, суспензии	лиофобные коллоидные растворы, суспензии, пасты, краски и т.д.
г	тв	г/тв	Твердые пены	пемза, пенопласт, активированный уголь, хлеб, пенобетон и т.д.
ж	тв	ж/тв	Твердые эмульсии	вода в парафине, минералы с жидкими включениями, пористые тела в жидкости
тв	тв	тв/тв	Твердые золи	сталь, чугун, цветные стекла, драгоценные камни

4. По межфазному взаимодействию - лиофильные и лиофобные системы (предложено Г. Фрейндлихом). Классификация пригодна только для систем с жидкой дисперсионной средой.

Лиофильные системы – в них дисперсная фаза взаимодействует с дисперсионной средой и при определенных условиях способна в ней растворяться – растворы коллоидных ПАВ, растворы ВМС. Свободная энергия системы DF < 0.

DF = DU – TdS ; DS _{смешения} > 0;

DU = W _ког - W _сольв ,

где W _ког - работа когезии;

W _сольв - работа сольватации.

При DU > 0, DU < 0 ÞTdS >DU . Эта группа характеризуется малым значением поверхностного натяжения на границе раздела фаз.

Лиофобные системы – в них дисперсная фаза не способна взаимодействовать с дисперсионной средой и растворяться в ней. Для них DF > 0. Диспергирование в этом случае совершается либо за счет внешней работы, либо за счет других процессов, идущих в системе спонтанно (химическая реакция) и характеризуется высоким значением поверхностного натяжения на границе раздела фаз, что соответствует малому значению энергии сольватации.

Существует две группы способов получения дисперсных систем:

1. Способы диспергирования заключаются в раздроблении тела до коллоидного состояния (мукомольное производство).

2. Способы конденсации заключаются в укрупнении частиц, атомов, молекул до частиц коллоидных размеров (химическая реакция с образованием осадка).

Молекулярно-кинетические свойства дисперсных систем

Все молекулярно-кинетические свойства вызваны хаотическим тепловым движением молекул дисперсионной среды, которое складывается из поступательного, вращательного и колебательного движения молекул.

Молекулы жидкой и газообразной дисперсионной среды находятся в постоянном движении и сталкиваются между собой. Среднее расстояние, проходимое молекулой до столкновения с соседней, называют средней длиной свободного пробега. Молекулы обладают различной кинетической энергией. При данной температуре среднее значение кинетической энергии молекул остается постоянным, составляя для одной молекулы и одного моля:

; ,

где m – масса одной молекулы;

M – масса одного моля;

v – скорость движения молекул;

k – константа Больцмана;

R – универсальная газовая постоянная.

Флуктуация значений кинетической энергии молекул дисперсионной среды (т.е. отклонение от среднего) и является причиной молекулярно-кинетических свойств.

Изучение молекулярно-кинетических свойств возможно в результате применения статистических методов исследования, действительных для систем, состоящих из множества элементов (молекул). Исходя из допущения о беспорядочности движения отдельных молекул, теория определяет наиболее вероятное сочетание для систем из множества объектов. Молекулярно-кинетические свойства проявляются в жидкой и газообразной среде, молекулы которых обладают определенно подвижностью.

Броуновское движение

Броуновским называют непрерывное, хаотическое, равновероятное для всех направлений движение мелких частиц, взвешенных в жидкостях или газах, за счет воздействия молекул дисперсионной среды.

Мельчайшие частицы незначительной массы испытывают неодинаковые удары со стороны молекул дисперсионной среды, возникает сила, движущая частицу, направление и импульс силы, непрерывно меняются, поэтому частица совершает хаотические движения.

Определили эти изменения и связали их с молекулярно-кинетическими свойствами среды в 1907 году А. Эйнштейн и М. Смолуховский. В основе расчета – не истинный путь частицы дисперсной фазы, а сдвиг частиц. Если путь частицы определяется ломаной линией, то сдвиг х характеризует изменение координат частицы за определенный отрезок времени. Средний сдвиг определяет среднеквадратичное смещение частицы:

,

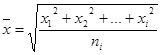где х ₁ , х ₂ , х _i – сдвиг частиц за определенное время.

Теория броуновского движения исходит из представления о взаимодействии случайной силы f (t), характеризующей удары молекул, силы F _t , зависящей от времени, и силы трения при движении частиц дисперсной фазы в дисперсионной среде со скоростью v. Уравнение броуровского движения (уравнение Ланжевена) имеет вид: , где m – масса частицы; h - коэффициент вязкости дисперсионной среды. Для больших промежутков времени (t>>m /h) инерцией частиц (m (dv / d t) можно пренебречь. После интегрирования уравнения 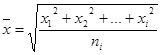при условии, что среднее произведение импульсов случайной силы равно нулю, среднее значение флуктуации (средний сдвиг) равно: 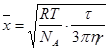, где t - время; r – радиус частиц дисперсной фазы; N _A – число Авогадро частиц.

В этой формуле характеризует молекулярно-кинетические свойства дисперсионной среды, h - ее вязкость, r – радиус частиц – параметр, относящийся к дисперсной фазе, а время t определяет взаимодействие дисперсионной среды с дисперсной фазой.

Кроме поступательного, возможно вращательное броуновское движение для двухмерных частиц и частиц неправильной формы (нитей, волокон, хлопьев и т.д.).

Броуновское движение наиболее интенсивно проявляется в высокодисперсных системах (размеры частиц 10^-9 ¸ 10^-7 м), несмотря на то, что молекулы дисперсионной среды действуют также и на частицы средне- и грубодисперсных систем. Но в связи со значительным размером частиц число ударов молекул резко увеличивается. По законам статистики, импульс действия сил со стороны молекул среды взаимно компенсируется, а значительная масса и инерция крупных частиц оставляет воздействие молекул без последствий.

Тема 1.1.2. Диффузия

Диффузией называют самопроизвольное распространение вещества из области с большей концентрацией в область с меньшей концентрацией. Различают следующие виды диффузии: молекулярную, ионную и коллоидных частиц.

Ионная диффузия связана с самопроизвольным перемещением ионов.

Диффузия высокодисперсных коллоидных частиц показана на рис. 1.1.2.1. В нижней части концентрация частиц больше, чем в верхней, т.е.

v₁ >v₂ (где , м³ – численная

концентрация частиц, N – число частиц дисперсной фазы, V _д.с. – объем дисперсной системы). Диффузия направлена из области с большей концентрации в область с меньшей концентрацией, т.е. снизу вверх (на рис. показано стрелкой). Диффузия характеризуется определенной скоростью перемещения вещества через поперечное сечение В , которая равна .

На расстоянии Dх разность концентраций составит v ₂ – v ₁ , т к. v ₁ >v ₂ , эта величина отрицательна. Изменение концентрации, отнесенное к единице расстояния, называют градиентом концентрации или (в дифф. форме) .

Скорость перемещения вещества пропорциональна градиенту концентрации и площади В , через которую происходит движение диффузионного потока, т.е.

; -

- основное уравнение диффузии в дифференциальной форме.

Скорость диффузии () величина положительная, а градиент концентрации - отрицателен.; поэтому перед правой частью уравнения – знак «минус». Коэффициент пропорциональности D – это коэффициент диффузии . Основное уравнение справедливо для всех видов диффузии , в т.ч. и для коллоидных частиц. В интегральной форме оно применимо для двух процессов – стационарного и нестационарного:

1) для стационарного процесса: =const. Значительное число диффузионных процессов близко к стационарным. Интегрируя , получим:

;

- I-й закон диффузии Фика.

Физический смысл коэффициента диффузии D: если -=1, В = 1 и t = 1, то m = D , т.е. коэффициент диффузии численно равен массе диффундирующего вещества, когда градиент концентрации, площадь сечения диффузионного потока и время равны единице. Равенство только численное, т.к. размерность коэффициента диффузии [м² /с] не соответствует размерности массы.

2) для нестационарного процесса: ¹const. Тогда интегрирование основного уравнения с учетом изменения градиента концентрации усложняется. При отсутствии в среде градиентов температуры, давления, электрического потенциала из уравнения определим массу вещества m₁ , переносимого в результате диффузии в единицу времени через единицу площади поверхности, перпендикулярной направлению переноса (В = 1 и t = 1): , с учетом которого можно определить пространственно-временное распределение концентрации:

- второй закон Фика.

На рис. представлена одномерная диффузия, определяющая движение вещества в одном направлении. Возможна также двух- и трехмерная диффузия вещества (диффузия вещества в двух и трех направлениях), описываемая уравнением: , где I – вектор плотности диффузионного потока; gradv – градиент поля концентрации.

Для трехмерной диффузии, по второму закону Фика, запишем: .

Для двумерной диффузии в правой части уравнения ограничиваемся выражениями для х и y .

Значения коэффициента диффузии для видов её распределяются так: ионная – D = 10^-8 м² /с; молекулярная - D = 10^-9 ; коллоидных частиц - D = 10^-10 . Отсюда видно, что диффузия коллоидных частиц затруднена по сравнению с двумя другими видами. Так, скорость диффузии частиц карамели (дисперсная фаза – коллоидный раствор) в 100 – 1000 раз меньше скорости диффузии молекул сахара (молекулярный раствор). Соответственно в газах D увеличивается до 10^-4 , в твердых телах снижается до 10^-12 м² /с.

Количественно диффузия определяется коэффициентом диффузии, связанным со средним сдвигом соотношением: ; - продолжительность диффузии.

Диффузия высокодисперсных частиц совершается беспорядочно с большей вероятностью в сторону меньшей концентрации. При выводе соотношения приняты следующие допущения: частицы дисперсной фазы движутся независимо друг от друга, между ними отсутствует взаимодействие; средняя энергия поступательных движений частиц равна 0,5 kT .

Используя формулу определения среднего сдвига, коэффициент диффузии можно представить в виде: (k – константа Больцмана, равная ). Если D известен, найдем размер частиц:

; Þ чем больше размер частиц, тем меньше коэффициент диффузии, менее интенсивна сама диффузия.

Диффузия в полной мере проявляется у высокодисперсных систем (10^-9 – 10^-7 м), ослаблена у среднедисперсных (10^-7 – 10^-5 м) и практически отсутствует у грубодисперсных систем (>10^-5 м). Коэффициент диффузии зависит и от формы частиц, что не учтено в уравнении . Поэтому формула определяет размер только коллоидных шарообразных частиц (или приведенный к шарообразному размер частиц неправильной формы).

Тема 1.2.3. Осмотическое давление

При разделении двух растворов различной концентрации или раствора и чистого растворителя полупроницаемой перегородкой (мембраной) возникает поток растворителя от меньшей концентрации к большей, выравнивающей концентрацию. Этот процесс называется осмосом .

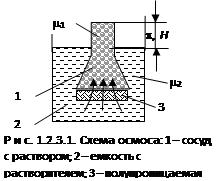
На схеме (рис. 1.2.3.1) в сосуд с полупроницаемой перегородкой 3, помещен раствор 1. Перегородка пропускает дисперсионную среду (растворитель), но является препятствием для коллоидных частиц (растворенных веществ). Снаружи перегородки – чистый растворитель 2. Концентрация раствора по обе стороны перегородки различна. Внутри сосуда 1 часть раствора занимают молекулы растворенного вещества (частицы дисперсной фазы) Þ концентрация растворителя там меньше, чем в емкости 2 с чистым растворителем.

За счет диффузии жидкость из области более высокой концентрации перемещается в область меньшей концентрации (из емкости 2 в сосуд 1). С кинетической точки зрения это обусловлено тем, что число ударов молекул о мембрану растворителя со стороны чистого или более разбавленного раствора больше, чем со стороны раствора, что и заставляет перемещаться растворитель через поры мембраны туда, где его меньше (т.е. в область раствора).

С термодинамической точки зрения , химический потенциал m₂ чистой жидкости больше m₁ растворителя в растворе, процесс самопроизвольно идет в сторону меньшего химического потенциала до их выравнивания: m₂ = m₁ .

В результате перемещения жидкости в емкости 1 создается избыточное давление p, называемое осмотическим. Растворитель, проникающий в область раствора 1, поднимает уровень жидкости на высоту Н , что компенсирует давление чистого растворителя в сторону раствора. Наступает момент, когда вес столба жидкости в области раствора уравнивается давлением растворителя.

Осмотическое давление – такое избыточное давление над раствором, которое необходимо для исключения переноса растворителя через мембрану. Осмотическое давление равно тому давлению, которое производила бы дисперсная фаза (растворенное вещество), если бы она в виде газа при той же температуре занимала тот же объем, что и коллоидная система (раствор)

Осмотическое давление p достаточно разбавленных коллоидных растворов может быть найдено по уравнению:

или - уравнение Вант-Гоффа

где m _{общ/ m} – масса растворенного вещества; m – масса одной частицы; V – объем частицы; N_A – число Авогадро; Т – абсолютная температура; n - частичная концентрация; k – постоянная Больцмана; М – масса одного моля растворенного вещества; с – массовая концентрация.