Название: Моделювання станів транзистора 2Т909Б

Вид работы: контрольная работа

Рубрика: Коммуникации и связь

Размер файла: 235.94 Kb

Скачать файл: referat.me-167768.docx

Краткое описание работы: Дослідження характеру залежності струму колектора від напруги на колекторно-емітерному переході і струму бази для вихідних вольт-амперних характеристик транзистора. Використання досліджуваного транзистора 2Т909Б у широкосмугових підсилювачах потужності.

Моделювання станів транзистора 2Т909Б

Міністерство освіти і науки України

Національний технічний університет України

«Київський політехнічний інститут»

Кафедра КЕОА

Розрахунково-графічна контрольна робота

з курсу:

«Моделювання станів транзистора 2Т909Б»

Об’єкт дослідження

Кремнієвий епітаксіально-планарний транзистор n-p-n типу 2Т909Б. Залежність струму колектора (I_к , А) від напруги колектор-емітер (U_ке , В) і струму бази (I_б , А).

Структура	n-p-n
Макс. напр. к-е при заданному тоці и заданному сопр. в цепи б-э.(Uкэr макс),В	60
Максимально допустимий ток к (Iк макс,А)	4
Гранична частота коефіціента передачі тока fгр,МГц	500.00
Максимальна розсіювальна потужність (Рк,Вт)	54
Корпус	KT-15

Мета дослідження

Дослідити характер залежності струму колектора I_к від напруги на колекторно-емітерному переході U_ке і струму бази І_б для вихідних ВАХ транзистора.

Актуальність дослідження

Транзистори широко використовуються в електронних приладах в якості підсилювачів. Вони виготовляються з метою застосування в якійсь конкретній області. Досліджуваний транзистор 2Т909Б (потужний, високочастотний, кремніевий, епитаксиально-планарний, структура n-p-n, використовуеться у широкополосних підсилювачів потужності)

Метод дослідження

Дослідження двофакторного виробничого процесу проводиться за допомогою метода регресійного аналізу. Його особливістю є те, що стан технічної системи описують функцією багатьох аргументів. Числове значення функції – параметр оптимізації Y, що залежить від факторів x_i , i = 1, 2 …. m, де m – номер фактора. Множина можливих сполучень факторів і їхніх значень визначає множину станів технічної системи.

Факторами можуть бути як незалежні змінні так і функції одного або декількох факторів (повнофакторний регресійний аналіз).

Функціональний зв’язок параметру Y з факторами x_i моделюють поліномом (рівнянням регресії):

Y = b₀ + b₁ x₁ + b₂ x₂ +...+ b_n x_n + b₁₂ x₁ x₂ + b₁₃ x₁ x₃ +…b_n-1,n x_n-1 x_n + …+ b_n+k x₁ ² + b_n+k+1 x₂ ² + … + b_m x_n ² + … = b₀ + b₁ x₁ + b₂ x₂ +... + b_n x_n +... + b_m x_m +… (1),

де x₁ , x₂ , x₃ ,..., x_n – фактори,

b₀ , b₁ , b₂ ,…, b_n – коефіцієнти.

Коефіцієнти регресії b_i визначають, виходячи з критерію мінімізації суми квадратів різниці між експериментально встановленими значеннями параметра y_j і модельним значенням параметра y_jmod у всіх експериментальних точках j = 1, 2, 3... N, де N – кількість дослідів. Необхідною умовою існування мінімуму є рівність . Вона визначає наявність екстремуму функції похибки апроксимації . Оскільки верхньої межі функція не має (похибка може бути як завгодно великою), умова є достатньою умовою існування мінімуму. Рівність нулю частинних похідних визначає систему n рівнянь з n невідомими, якими є коефіцієнти b_i рівняння регресії. Після розкриття дужок, зведення подібних членів і перегрупування одночленів система рівнянь набуває вигляду:

Ліву частину системи рівнянь можна представити добутком трьох матриць (X^T X)B, а праву добутком двох матриць X^T Y,

де Х – матриця умов,

X^T – транспонована матриця Х,

В – матриця коефіцієнтів,

Y – матриця результатів (матриця станів),

x_kl – значення k-го фактора в l-му досліді.

X = 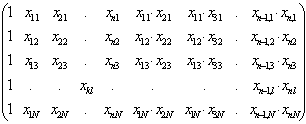, B = , Y = .

У матричному вигляді систему записують рівнянням (X^T X)B = X^T Y. З останнього рівняння очевидно, що коефіцієнти b_i визначаються як , де (X^T X)^-1 – обернена матриця (X^T X). Дисперсію моделювання оцінюють за формулою:

δ_мод ² = ,

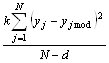де N - кількість дослідів,

d – кількість значущих коефіцієнтів моделі

k – кратність дублювання дослідів

Експериментальні дані та їх обробка

Математичну модель процесу представимо у вигляді полінома, а саме:

Y’ = b₀ + b₁ U_ке + b₂ I_б + b₃ U_ке I_б + b₄ U_ке ² + b₅ I_б ² + b₆ U_ке ² I_б + b₇ I_б ² U_ке +

+ b₈ U_ке ² I_б ^2,

де Y’ – розрахункове значення струму колектора І_к (мА),

b₀ , b₁ … – коефіцієнти поліному,

U_ке – напруга на колекторно-емітерному переході (В),

I_б – струм бази І_б (мА).

Сімейство ВАХ транзистора 2Т909Б має наступний вигляд (рис.1)

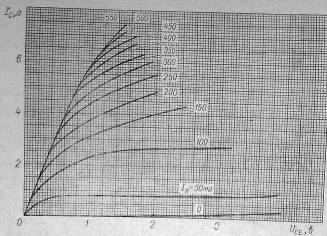
Рис. 1. Вольт-амперні характеристики транзистора 2Т909Б.

Отримані експериментальні данні наведено в табл. 1.

Таблиця 1. Експериментальна залежність І_К (мА) від І_Б та U_КЕ для транзистора 2Т909Б

x0	x1(Iб)	x2(Uк-э)	x1*x2	X1^2	x2^2	x1*x2^2	x1^2*x2	(x1*x2)^2	Y
1	0,05	0,2	0,01	0,0025	0,04	0,002	0,0005	0,0001	0,5
1	0,05	0,4	0,02	0,0025	0,16	0,008	0,001	0,0004	0,7
1	0,05	0,6	0,03	0,0025	0,36	0,018	0,0015	0,0009	0,8
1	0,05	0,8	0,04	0,0025	0,64	0,032	0,002	0,0016	0,8
1	0,05	1	0,05	0,0025	1	0,05	0,0025	0,0025	0,8
1	0,05	1,2	0,06	0,0025	1,44	0,072	0,003	0,0036	0,8
1	0,05	1,4	0,07	0,0025	1,96	0,098	0,0035	0,0049	0,8
1	0,05	1,6	0,08	0,0025	2,56	0,128	0,004	0,0064	0,8
1	0,05	1,8	0,09	0,0025	3,24	0,162	0,0045	0,0081	0,8
1	0,05	2	0,1	0,0025	4	0,2	0,005	0,01	0,8
1	0,1	0,2	0,02	0,01	0,04	0,004	0,002	0,0004	1
1	0,1	0,4	0,04	0,01	0,16	0,016	0,004	0,0016	1,5
1	0,1	0,6	0,06	0,01	0,36	0,036	0,006	0,0036	1,8
1	0,1	0,8	0,08	0,01	0,64	0,064	0,008	0,0064	2,1
1	0,1	1	0,1	0,01	1	0,1	0,01	0,01	2,3
1	0,1	1,2	0,12	0,01	1,44	0,144	0,012	0,0144	2,5
1	0,1	1,4	0,14	0,01	1,96	0,196	0,014	0,0196	2,6
1	0,1	1,6	0,16	0,01	2,56	0,256	0,016	0,0256	2,7
1	0,1	1,8	0,18	0,01	3,24	0,324	0,018	0,0324	2,7
1	0,1	2	0,2	0,01	4	0,4	0,02	0,04	2,7
1	0,15	0,2	0,03	0,0225	0,04	0,006	0,0045	0,0009	1,2
1	0,15	0,4	0,06	0,0225	0,16	0,024	0,009	0,0036	2
1	0,15	0,6	0,09	0,0225	0,36	0,054	0,0135	0,0081	2,5
1	0,15	0,8	0,12	0,0225	0,64	0,096	0,018	0,0144	2,9
1	0,15	1	0,15	0,0225	1	0,15	0,0225	0,0225	3,1
1	0,15	1,2	0,18	0,0225	1,44	0,216	0,027	0,0324	3,3
1	0,15	1,4	0,21	0,0225	1,96	0,294	0,0315	0,0441	3,5
1	0,15	1,6	0,24	0,0225	2,56	0,384	0,036	0,0576	3,7
1	0,15	1,8	0,27	0,0225	3,24	0,486	0,0405	0,0729	3,9
1	0,15	2	0,3	0,0225	4	0,6	0,045	0,09	4
1	0,2	0,2	0,04	0,04	0,04	0,008	0,008	0,0016	1,2
1	0,2	0,4	0,08	0,04	0,16	0,032	0,016	0,0064	2,6
1	0,2	0,6	0,12	0,04	0,36	0,072	0,024	0,0144	3
1	0,2	0,8	0,16	0,04	0,64	0,128	0,032	0,0256	3,4
1	0,2	1	0,2	0,04	1	0,2	0,04	0,04	3,8
1	0,2	1,2	0,24	0,04	1,44	0,288	0,048	0,0576	4
1	0,2	1,4	0,28	0,04	1,96	0,392	0,056	0,0784	4,3
1	0,2	1,6	0,32	0,04	2,56	0,512	0,064	0,1024	4,5
1	0,2	1,8	0,36	0,04	3,24	0,648	0,072	0,1296	4,7
1	0,2	2	0,4	0,04	4	0,8	0,08	0,16	4,9
1	0,25	0,2	0,05	0,0625	0,04	0,01	0,0125	0,0025	1,2
1	0,25	0,4	0,1	0,0625	0,16	0,04	0,025	0,01	2,6
1	0,25	0,6	0,15	0,0625	0,36	0,09	0,0375	0,0225	3,5
1	0,25	0,8	0,2	0,0625	0,64	0,16	0,05	0,04	4
1	0,25	1	0,25	0,0625	1	0,25	0,0625	0,0625	4,4
1	0,25	1,2	0,3	0,0625	1,44	0,36	0,075	0,09	4,7
1	0,25	1,4	0,35	0,0625	1,96	0,49	0,0875	0,1225	4,9
1	0,25	1,6	0,4	0,0625	2,56	0,64	0,1	0,16	5,2
1	0,25	1,8	0,45	0,0625	3,24	0,81	0,1125	0,2025	5,4
1	0,25	2	0,5	0,0625	4	1	0,125	0,25	5,5
1	0,3	0,2	0,06	0,09	0,04	0,012	0,018	0,0036	1,2
1	0,3	0,4	0,12	0,09	0,16	0,048	0,036	0,0144	2,6
1	0,3	0,6	0,18	0,09	0,36	0,108	0,054	0,0324	3,8
1	0,3	0,8	0,24	0,09	0,64	0,192	0,072	0,0576	4,4
1	0,3	1	0,3	0,09	1	0,3	0,09	0,09	4,8
1	0,3	1,2	0,36	0,09	1,44	0,432	0,108	0,1296	5,2
1	0,3	1,4	0,42	0,09	1,96	0,588	0,126	0,1764	5,4
1	0,3	1,6	0,48	0,09	2,56	0,768	0,144	0,2304	5,7
1	0,3	1,8	0,54	0,09	3,24	0,972	0,162	0,2916	5,9
1	0,35	0,2	0,07	0,1225	0,04	0,014	0,0245	0,0049	1,2
1	0,35	0,4	0,14	0,1225	0,16	0,056	0,049	0,0196	2,6
1	0,35	0,6	0,21	0,1225	0,36	0,126	0,0735	0,0441	3,8
1	0,35	0,8	0,28	0,1225	0,64	0,224	0,098	0,0784	4,8
1	0,35	1	0,35	0,1225	1	0,35	0,1225	0,1225	5,3
1	0,35	1,2	0,42	0,1225	1,44	0,504	0,147	0,1764	5,6
1	0,35	1,4	0,49	0,1225	1,96	0,686	0,1715	0,2401	5,9
1	0,35	1,6	0,56	0,1225	2,56	0,896	0,196	0,3136	6,1
1	0,35	1,8	0,63	0,1225	3,24	1,134	0,2205	0,3969	6,3
1	0,4	0,2	0,08	0,16	0,04	0,016	0,032	0,0064	1,2
1	0,4	0,4	0,16	0,16	0,16	0,064	0,064	0,0256	2,6
1	0,4	0,6	0,24	0,16	0,36	0,144	0,096	0,0576	3,8
1	0,4	0,8	0,32	0,16	0,64	0,256	0,128	0,1024	4,9
1	0,4	1	0,4	0,16	1	0,4	0,16	0,16	5,6
1	0,4	1,2	0,48	0,16	1,44	0,576	0,192	0,2304	6
1	0,4	1,4	0,56	0,16	1,96	0,784	0,224	0,3136	6,3
1	0,4	1,6	0,64	0,16	2,56	1,024	0,256	0,4096	6,6

Скористаємося цією таблицею для визначення функції відгуку, яка встановлює аналітичний зв’язок між І_К – параметром оптимізації і незалежними змінними І_Б , U_КЕ – факторами. Для цього формуємо матрицю Х – вектор значення факторів, матрицю Y – відгук технічної системи. Далі знаходимо матрицю (Х^Т · Х)^-1 , яка називається матрицею похибок або матрицею коваріацій. Вона має наступний вигляд:

(ХТ * Х)^-1

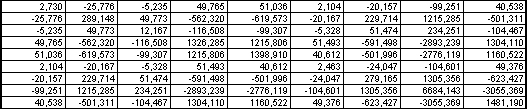
Рис. 2 Матриця коваріацій для моделі

Виходячи з отриманих даних знайдемо коефіцієнти поліному b_i . Матриця коефіцієнтів В = (Х^Т * Х)^-1 * (Х^T * Y) має вигляд (рис.3)

B0	0,144
B1	7,649
B2	-0,185
B3	20,067
B4	-24,031
B5	-0,193
B6	-1,604
B7	8,677
B8	-14,015

Рис. 3. Матриця коефіцієнтів В

Отже, математична модель залежності I_к (U_ке , І_б ) буде представлена наступною функцією:

Y’ = 0,144+ 7,649I_б -0,185 U_ке + 20,066U_ке I_б – 24.0314I_б ² – 0.193U_ке ² –

–1,604U_ке ² I_б + 8,677I_б ² U_ке – 14,015U_ке ² I_б ²

Розраховуємо значення І_К по отриманому рівнянню моделі Отримані данні наведені нижче у таблиці 2.

Таблиця 2. Залежність І_К від І_Б та U_КЕ для транзистора 2Т909Б, отримана по рівнянню моделі.

Iб	Uк-э	Y	Ymod	Delta^2
0,05	0,2	0,5	0,622065	0,0149
0,05	0,4	0,7	0,753084	0,002818
0,05	0,6	0,8	0,859469	0,003537
0,05	0,8	0,8	0,941222	0,019944
0,05	1	0,8	0,998341	0,039339
0,05	1,2	0,8	1,030827	0,053281
0,05	1,4	0,8	1,03868	0,056968
0,05	1,6	0,8	1,021899	0,049239
0,05	1,8	0,8	0,980486	0,032575
0,05	2	0,8	0,914439	0,013096
0,1	0,2	1	1,030545	0,000933
0,1	0,4	1,5	1,35301	0,021606
0,1	0,6	1,8	1,636018	0,02689
0,1	0,8	2,1	1,879569	0,04859
0,1	1	2,3	2,083663	0,046802
0,1	1,2	2,5	2,248299	0,063353
0,1	1,4	2,6	2,373479	0,051312
0,1	1,6	2,7	2,459202	0,057984
0,1	1,8	2,7	2,505468	0,037843
0,1	2	2,7	2,512276	0,03524
0,15	0,2	1,2	1,324743	0,015561
0,15	0,4	2	1,838922	0,025946
0,15	0,6	2,5	2,293215	0,04276
0,15	0,8	2,9	2,687621	0,045105
0,15	1	3,1	3,02214	0,006062
0,15	1,2	3,3	3,296773	1,04E-05
0,15	1,4	3,5	3,511519	0,000133
0,15	1,6	3,7	3,666378	0,00113
0,15	1,8	3,9	3,761351	0,019224
0,15	2	4	3,796437	0,041438
0,2	0,2	1,2	1,504657	0,092816
0,2	0,4	2,6	2,21082	0,151461
0,2	0,6	3	2,83106	0,028541
0,2	0,8	3,4	3,365378	0,001199
0,2	1	3,8	3,813774	0,00019
0,2	1,2	4	4,176248	0,031063
0,2	1,4	4,3	4,4528	0,023348
0,2	1,6	4,5	4,643429	0,020572
0,2	1,8	4,7	4,748137	0,002317
0,2	2	4,9	4,766922	0,01771
0,25	0,2	1,2	1,570289	0,137114
0,25	0,4	2,6	2,468703	0,017239
0,25	0,6	3,5	3,249553	0,062724
0,25	0,8	4	3,91284	0,007597
0,25	1	4,4	4,458564	0,00343
0,25	1,2	4,7	4,886724	0,034866
0,25	1,4	4,9	5,197321	0,0884
0,25	1,6	5,2	5,390354	0,036235
0,25	1,8	5,4	5,465824	0,004333
0,25	2	5,5	5,423731	0,005817
0,3	0,2	1,2	1,521638	0,103451
0,3	0,4	2,6	2,612571	0,000158
0,3	0,6	3,8	3,548695	0,063154
0,3	0,8	4,4	4,330007	0,004899
0,3	1	4,8	4,95651	0,024495
0,3	1,2	5,2	5,428201	0,052076
0,3	1,4	5,4	5,745083	0,119082
0,3	1,6	5,7	5,907153	0,042912
0,3	1,8	5,9	5,914414	0,000208
0,35	0,2	1,2	1,358704	0,025187
0,35	0,4	2,6	2,642426	0,0018
0,35	0,6	3,8	3,728484	0,005115
0,35	0,8	4,8	4,61688	0,033533
0,35	1	5,3	5,307611	5,79E-05
0,35	1,2	5,6	5,80068	0,040272
0,35	1,4	5,9	6,096085	0,038449
0,35	1,6	6,1	6,193827	0,008803
0,35	1,8	6,3	6,093905	0,042475
0,4	0,2	1,2	1,081487	0,014045
0,4	0,4	2,6	2,558265	0,001742
0,4	0,6	3,8	3,788922	0,000123
0,4	0,8	4,9	4,773457	0,016013
0,4	1	5,6	5,511869	0,007767
0,4	1,2	6	6,00416	1,73E-05
0,4	1,4	6,3	6,250328	0,002467
0,4	1,6	6,6	6,250374	0,122238

Порівняємо наші результати, а саме експериментальні з отриманими по рівнянню моделі. Для цього побудуємо вольт-амперні характеристики та поверхні, що відображають поведінку нашої системи.

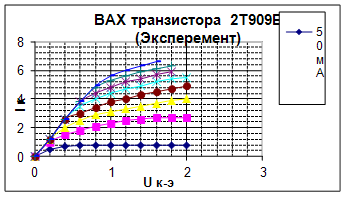
Рис. 4. ВАХ транзистора 2Т909Б, побудована по експериментальним даним

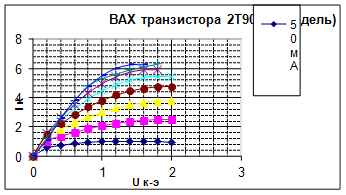
Рис. 5. ВАХ транзистора 2Т909Б, побудована на основі модельних даних

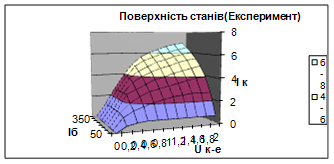
Рис. 6. Поверхня станів транзистора 2Т909Б, побудована по експериментальним даним

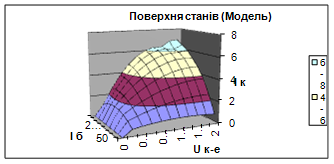
Рис. 7. Поверхня станів транзистора 2Т909Б, побудована на основі модельних даних

Приймаємо, що дисперсія експерименту σ_y ² = 0,05 А.

Домноживши матрицю коваріацій на σ_y ² отримаємо (табл. 3):

Таблиця 3 Матриця коваріацій помножена на σ_y ²

σ_y ² ·(Х^Т ·Х)^-1

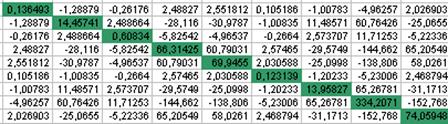
Тепер значущість коефіцієнтів регресії можна оцінити за допомогою критерія Стьюдента. Скористаємось наступною формулою:

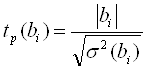
Табличне значення критерію Стьюдента для числа ступенів свободи n₀ = 8 – 1 = 7, складає t_т = 2,365. Оцінимо статистичну значущість кожного з коефіцієнтів:

tp0	0,38988226
tp1	2,01166266
tp2	0,23743137
tp3	2,46416891
tp4	2,87342414
tp5	0,54897414
tp6	0,42926849
tp7	0,47464611
tp8	1,62850119

Як видно із отриманих значень t_p для кожного з коефіцієнтів, порівнявши їх з табличним значенням 2,365, помітно, що коефіцієнти t_p3 , t_p4 менше табличного значення. Але вони є статистично зв’язаними з іншими коефіціентами, а значить вони є статистично значущими і не мають бути рівними нулю. Також матриця коваріацій не є ортогональною.

Отже модель залишається незмінною, а саме:

Y’ = 0,144+ 7,649I_б -0,185 U_ке + 20,066U_ке I_б – 24.0314I_б ² – 0.193U_ке ² –

–1,604U_ке ² I_б + 8,677I_б ² U_ке – 14,015U_ке ² I_б ²

На основі отриманих значень моделі обчислимо дисперсію:

σ_мод ² = ,

де k – кратність дублювання,

N – кількість дослідів,

d – кількість значущих коефіцієнтів моделі.

σ_мод ² = 2,4113 / (76-2) = 0,03258.

Перевіримо статистичну гіпотезу про адекватність моделі станів транзистора 2Т909Б за допомогою критерію Фішера.

Розрахуємо значення критерію Фішера, виходячи з того, що це є відношення більшої з двох дисперсій до меншої, причому воно завжди більше за одиницю.

F_p = σ_мод ² (σ_y ² )/ σ_y ² (σ_мод ² );

Нехай похибка виміру за допомогою лінійки складає 0,5 мм. Враховуючи, що вся вісь І_к 136 мм - 483 мА, отримуємо σ_y ≈ 1,7757 мА, тобто дисперсія експерименту σ_y ² = 3,1532. Таким чином дисперсія експерименту складає σ_y ² = 3,1532, у той час як дисперсія моделі в свою чергу складає σ_мод ² = 8,664. Легко бачити, що дисперсія моделі більша, тому визначимо розрахункове значення критерію Фішера згідно приведеної вище формули:

F_p = 0,05 / 0,03258 ≈ 1,5346.

Табличне значення критерію Фішера складає:

F_T ≈ 3,29046. Тобто F_p < F_T , що говорить про те, що модель експерименту є адекватною.

Висновок

В даній розрахунково-графічній роботі мною були обрані вихідні ВАХ транзистора 2Т909Б у якості приклада дослідження двофакторного технічного процесу. Дані були взяті з довідника.

Спочатку було знято експериментальні дані вихідних ВАХ транзистора, тобто залежність І_к (Uк-е, І_б ) і складенна таблиця початкових даних.

Потім в якості моделі було взято функцію

Y’ = b₀ + b₁ U_ке + b₂ I_б + b₃ U_ке I_б + b₄ U_ке ² + b₅ I_б ² + b₆ U_ке ² I_б + b₇ I_б ² U_ке +

+ b₈ U_ке ² I_б ^2,

Розраховано її коефіцієнти за допомогогю регресійного аналізу, побудовано графіки та поверхні станів і обчислено дисперсію експерименту,яка склала σ_y ² ≈ 3,1532.

На другому етапі було проведено оцінку статистичної значущості коефіцієнтів регресії за допомогою критерію Стьюдента. В результаті чого отримали, що коефіцієнти b₀ ,b₁ , b₂ , b₅ , b₆ , b₇ , b₈ є статистично незначущими, але прирівняти до нуля їх не можна, оскільки вони статистично зв’язані з іншими коефіцієнтами матриці коваріацій. Таким чином, рівняння моделі не змінилося.

На завершальному етапі роботи було перевірено статистичну гіпотезу про адекватність моделі станів технічної системи за допомогою критерію Фішера. Спочатку було знайдено розрахункове значення критерію Фішера: на основі двох значень дисперсії - теоретичної і експериментальної (поділили більшу σ_y ² на меншу σ_мод ² з них), отримали F_p ≈ 1,389391. Потім з таблиці вибрали відповідне значення критерію Фішера F_T ≈ 3,29046 і порівняли з розрахунковим, в результаті чого упевнились, що F_p < F_T , тобто модель є адекватною.

Література

1. П.О. Яганов, «Регресійний аналіз багатофакторних систем»-K.:НТУУ «КПІ»,2006-35с.