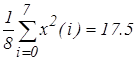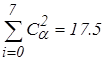Название: Двоично-ортогональные системы базисных функций

Вид работы: реферат

Рубрика: Коммуникации и связь

Размер файла: 63.24 Kb

Скачать файл: referat.me-169646.docx

Краткое описание работы: Курс: Теория информации и кодирования Тема: ДВОИЧНО-ОРТОГОНАЛЬНЫЕ СИСТЕМЫ БАЗИСНЫХ ФУНКЦИЙ Содержание Введение ФУНКЦИИ РАДЕМАХЕРА ФУНКЦИИ УОЛША

Двоично-ортогональные системы базисных функций

Курс: Теория информации и кодирования

Тема: ДВОИЧНО-ОРТОГОНАЛЬНЫЕ СИСТЕМЫ БАЗИСНЫХ ФУНКЦИЙ

Содержание

Введение

1. ФУНКЦИИ РАДЕМАХЕРА

2. ФУНКЦИИ УОЛША

3. ПРЕОБРАЗОВАНИЕ УОЛША

4. ДИСКРЕТНОЕ ПРЕОБРАЗОВАНИЕ УОЛША

Список литературы

Введение

Широкое использование спектрально-частотного представления процессов при исследовании сигналов и систем (преобразование Фурье) связанно с тем, что при гармонических воздействиях колебания сохраняют свою форму при прохождении через линейные цепи (системы) и отличаются от входных только амплитудой и фазой. Это свойство используют ряд методов исследования систем (например, частотные методы).

Но при реализации алгоритмов, использующих преобразование Фурье на ЭВМ, необходимо выполнять большое количество операций умножения (миллионы и миллиарды), что занимает большое количество машинного времени.

В связи с развитием средств вычислительной техники и применения их для обработки сигналов широко используются преобразования, содержащие в качестве ортогонального базиса кусочно-постоянные, знакопеременные функции. Эти функции легко реализуются с помощью средств вычислительной техники (аппаратно или программно) и их использование позволяет свести к минимуму время машинной обработки (за счет исключения операции умножения).

К числу таких преобразований можно отнести преобразования Уолша и Хаара, которые широко используются в области управления и связи. В области компьютерной технике эти преобразования используются при анализе и синтезе устройств логического типа, комбинационных схем особенно использующих большие и сверхбольшие интегральные схемы (БИС и СБИС), содержащие сотни тысяч элементов, выполняющих различные логические функции. Преобразования Уолша и Хаара используют кусочно-постоянные функции Уолша, Радемахера, и др., принимающие значения ±1, либо Хаара, принимающие значения ±1 и 0 на интервале определения [-0,5, 0,5] либо [0, 1].

Все эти системы взаимосвязаны и каждую из них можно получить как линейную комбинацию из другой (например: система Радемахера- составная часть системы Уолша). Обозначение функций связанных с авторами этих функций:

Уолша - Walsh - wal(n, Q),

Хаара- Haar- har(l, n ,Q),

Радемахера- Rademacher - rad(m, Q),

Адамара - Hadamard - had(h, Q),

Пели- Paley - pal(p, Q).

Все эти системы функции представляют собой системы двоично–ортогональных базисных функций.

1. Функции Радемахера

Функции Радемахера можно определить по формуле :

rad(m,Q) = sign[sin(2^m p Q)], (1)

где 0 £ Q < 1 - интервал определения; m - номер функции; m = 0, 1, 2, ...

Для m = 0 функция Радемахера rad(0,Q) = 1.

Знаковая функция sign(x) определяется соотношением

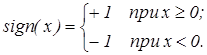(2)

Функции Радемахера это периодические функции с периодом 1, т. е.

rad(m,Q) = rad(m,Q+1) .

Первые четыре функции Радемахера показаны на рис. 1.

1

0 rad(0, Q)

-1

1

0 rad(1, Q)

-1

1

0 rad(2, Q)

-1

1 rad(3, Q)

0

-1

Q

0 0.51

Рис. 1. Функции Радемахера

Дискретные функции Радемахера определяются дискретными значениями Q в точках отсчета. Например: Rad(2,Q) = 1, 1, -1, -1, 1, 1, -1, -1.

Функции Радемахера ортогональные, ортонормированные (3) но являются нечетными, а значит, не образуют полную систему функций, т. к. существуют и другие функции ортогональные функциям Радемахера (например: rad(m,Q) = sign[cos(2^m p Q)]) поэтому их применение ограничено.

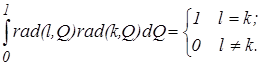(3)

Полными двоично-ортогональными системами базисных функций являются системы функций Уолша и Хаара.

2. Функции Уолша

Функции Уолша представляют собой полную систему ортогональных, ортонормированных функций. Обозначение: wal(n, Q) , где n - номер функции, при этом: n = 0, 1,... N-1; N = 2ⁱ ; i = 1, 2,… .

Первые 8 функций Уолша приведены на рис. 2.

1

0 wal(0, Q)

-1

1

0 wal(1, Q)

-1

1

0 wal(2, Q)

-1

1

0 wal(3, Q)

-1

1

0 wal(4, Q)

-1

1 wal(5,Q)

0

-1

1wal(6,Q)

0

-1

1 wal(7,Q)

0

-1

Q

0 0.5 1

Рис. 2. Функции Уолша

Функция Уолша имеет ранг и порядок. Ранг –число единиц в двоичном представлении n. Порядок - максимальный из содержащих единицу номер разряда двоичного представления. Например, функция wal(5,Q) имеет ранг- 2 а порядок –3 (n = 5 Þ 101).

Функции Уолша обладают свойством мультипликативности. Это значит, что произведение любых двух функций Уолша также является функцией Уолша: wal(k,Q)wal(l,Q)= wal(p,Q), где p = k Å l. В связи с возможностью применения к функциям Уолша логических операций, они широко используются в многоканальной связи с разделением по форме (используется также временное, частотное, фазовое и т. д. разделение), а также аппаратуре формирования и преобразования сигналов на базе микропроцессорной техники.

Функции Уолша можно получить как произведение функций Радема-хера, номер которых соответствует коду Грея номера функции Уолша. Соответствия для первых 8 функций Уолша приведены в табл. 1.

Таблица 1

N	Двоичный код n	Код Грея	Соотношения
0	000	000	wal(0,Q)=1
1	001	001	wal(1,Q)=rad(1,Q)
2	010	011	wal(2,Q)=rad(1,Q)×rad(2,Q)
3	011	010	wal(3,Q)=rad(2,Q)
4	100	110	wal(4,Q)=rad(2,Q)×rad(3,Q)
5	101	111	wal(5,Q)=rad(1,Q)×rad(2,Q)×rad(3,Q)
6	110	101	wal(6,Q)=rad(1,Q)×rad(3,Q)
7	111	100	wal(7,Q)=rad(3,Q)

Существуют различные способы упорядочения функций Уолша: по Уолшу (естественное), по Пэли, по Адамару. Нумерация функций Уолша при различных способах упорядочения (n - по Уолшу; p - по Пэли; h - по Адамару) приведена в табл. 2.

При упорядочение по Пэли номер функции определяется, как номер двоичного кода Грея прочитанный, как обычный двоичный код. Такое упорядочение называется диадическим.

При упорядочение по Адамару номер функции определяется, как двоичное представление номера функции Уолша системы Пели, прочитанное в обратном порядке такое упорядочение называется естественным.

Таблица 2

n	0	1	2	3	4	5	6	7
p	0	1	3	2	6	7	5	4
h	0	4	6	2	3	7	5	1

Как видно из таблицы, различные системы используют одни и те же функции Уолша в различной последовательности, которые равнозначны для представления сигналов, но отличаются только свойства разложения (например, функции Уолша - Пэли сходятся быстрее). При этом, каждому виду упорядочений соответствуют определенные формулы.

3. Преобразование Уолша

Рассмотрим спектральное представление сигналов с использованием базиса Уолша. Аналогично с рядом Фурье ряд Уолша имеет вид:

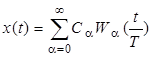, (4)

где спектр Уолша

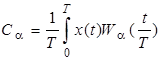. (5)

Для проверки правильности расчета спектральных коэффициентов может быть использовано равенство Парсеваля

.

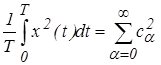Если ограничиться N членами в разложении, то получим усеченный ряд Уолша:

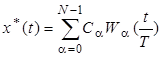,(6)

гдеt Î [0,T]; N=T/ D t; t = a D t приt ® ¥ a ® ¥ , a - сдвигпооси;

wal(n,Q) после преобразования аргументов.

Для практических расчетов можно использовать формулу:

.

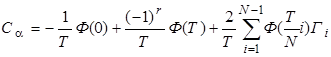где: ; (7)

r - ранг спектрального коэффициента с номером a (число двоичных разрядов числа a в которых имеются 1).

i - номер подынтервала определения функции x(t) ;

. (8)

Приэтом Г_i принимает значение ±1 или 0 в зависимости от того меняет ли W _a (i/N) в точке i/N знак с "+" на "-",c "-" на " +" или знак не меняется.

Пример 1. Разложить функцию x(t) = at в ряд по упорядоченным по Пэли функциям Уолша при N=8, T=1, a=1.

Решение: Определим Ф(t):

.

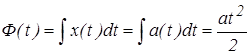Определим спектральные коэффициенты с учетом функций Уолша упорядоченным по Пэли по формуле (7)

C₀ = aT/2;

C₁ = -aT/2 + 0 +0 + 0 +2(aT/4) + 0 + 0 + 0 = -aT/4;

C₂ = -aT/2 + 0 + 4aT/64) + 0 - 16aT/64 + 0 +36aT/64 +0 =-aT/8;

C₃ = aT/2 + 0 + 4aT/64) + 0 + 0 + 0 - 36aT/64 +0 = 0;

C₄ =-aT/2 + aT/64 - 4aT/64 + 9aT/64 - 16aT/64 + 25aT/64 –

- 36aT/64 + 49aT/64 =-aT/16;

C₅ =C₆ =C₇ =0.

Ряд Уолша - Пэли имеет вид:

.

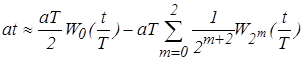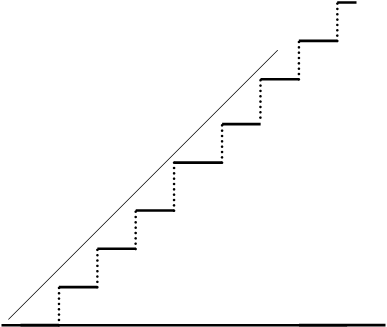
Аппроксимация функции x(t) = at при а=1 и t=1 полученным рядом приведена на рис. 3.

X

1

0 1 t

Рис . 3. Аппроксимация функции x(t)=at рядом Уолша – Пэли

4. Дискретное преобразование Уолша

Дискретное преобразование Уолша (ДПУ) производится при использовании дискретных функций Уолша W _a (i/N) Þ Wal(n, Q) и выполняется над решетчатыми сигналами x(i) , при этом число отсчетов N должно быть двоично -рациональным, т. е. N = 2ⁿ , где n = 1, 2,... , i - определяет номер точки дискретного интервала определения a = 0, 1,..., N-1 .

Формулы дискретного ряда Уолша имеют вид:

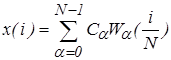,(9)

где дискретный спектр Уолша

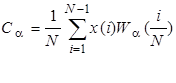. (10)

Для проверки правильности расчета спектральных коэффициентов может быть использовано равенство Парсеваля:

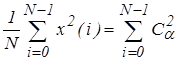(11)

График дискретной функции Уолша, упорядоченных по Пели приведен на рис.

W₀

012 3 4 5 6 7i

W₁

W₂

W₃

W₄

W₅

W₆

W₇

Рис. 4 График дискретной функции Уолша

Для ускорения дискретных преобразований Уолша используются алгоритмы быстрого преобразования Уолша (БПУ) аналогичного БПФ.

БПУ также производится прореживанием по времени и частоте.

Применение преобразований Уолша. Преобразования Уолша находят широкое применение при:

- построении цифровых фильтров;

- исследовании систем автоматического управления (моделировании, оптимизации, идентификации и т. д.);

- формировании сигналов;

- анализе и синтезе логических устройств (в теории цифровых автоматов).

Пример 2. Найти спектр Уолша - Пэли для дискретного сигнала

x(i) = i, N = 8, i = 0, 1, ...,7 .

Используя формулу для C _a при N=8 , в соответствии с графиком дискретной функции Уолша , приведенной на рис. 4, можно найти спектр Уолша (таб. 3).

Таблица 3

Значения функций и спектральных коеф. при значениях индексов i и a
0	1	2	3	4	5	6	7
x(i)=i	0	1	2	3	4	5	6	7
Ca	3,5	-2	-1	0	-0,5	0	0	0

Список литературы

1. Коганов А.В. Векторные меры сложности, энтропии, информации. “Математика. Компьютер. Образование”. Вып. 7, ч. 2, “Прогресс-Традиция”, М., 2000, с. 540 — 546

2. Гольдштейн А.Л. Теория принятия решений. Задачи и методы исследования операций и принятия решений: Учеб. пособие для вузов. - Пермь: Изд-во ПГТУ, 2004.-360 с.

3. Абдулгамидов А.Р., “О системах Хаара, Радемахера и Уолша функций многих переменных”, Функциональный анализ и теория функций. 6, Учён. зап. Казан. гос. ун-та, 129, № 3, Изд-во Казанского ун-та, Казань, 1969, 53–59

4. Малозёмов В.Н., Машарский С.М. Основы дискретного гармонического анализа. Часть вторая. СПб.: НИИММ, 2003. 100 с.

5. Львович А.А., Кузьмин Б.Д. Аналитическое выражение для спектров функций Уолша // Радиотехника. 1980. Т. 35. № 1. С. 33–39.

6. Зеленков А.В. Быстрое преобразование спектра сигнала из базиса Уолша в базис дискретных экспоненциальных функций // Радиотехника и электроника. 1977. Т. 27. № 3. С. 552–565.

7. Пойда В.Н. Спектральный анализ в дискретных ортогональных базисах. Минск: Наука и техника, 1978. 136 с.