Referat.me
/ / Управление многомерными автоматическими системами

Название: Управление многомерными автоматическими системами

Вид работы: контрольная работа

Рубрика: Коммуникации и связь

Размер файла: 22.66 Kb

Скачать файл: referat.me-170178.docx

Краткое описание работы: Характеристика структурной схемы объекта управления, особенности системы автоматического управления второго порядка. Составление уравнения объекта управления в векторной форме, порядок проверки системы на устойчивость, управляемость и наблюдаемость.

Управление многомерными автоматическими системами

МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ОТКРЫТЫЙ УНИВЕРСИТЕТ

ФАКУЛЬТЕТ ИНФОРМАТИКИ И РАДИОЭЛЕКТРОНИКИ

КАФЕДРА ИНФОРМАТИКИ И РАДИОЭЛЕТРОНИКИ

Контрольная работа

по управлению многомерными автоматическими системами

Выполнила: Ратникова С.А.

Заочная форма обучения

Курс V

Специальность 210100

№ зачетной книжки 6001053

Проверил преподаватель:

Работа сдана ____________________

Подпись лица, принявшего работу ____

Подпись студента ______________

Волоколамск 2004 г.

Исходные данные

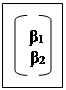
Структурная схема объекта управления – система автоматического управления второго порядка с одномерным вектором ū-входных воздействий и одномерным вектором y-выходных переменных приведена на рисунке:


(с1 с2 )
ū ν
∫
Ä S x y

α11 α12

α21 α22

R


α11 = 18

α12 = 5

α21 = – 3

α22 = 12

β1 = 1

β2 = – 2

c1 = – 1

c2 = 9

Задание

1. Записать уравнение объекта в векторной форме;

2. Исследовать объект управления на устойчивость;

3. Исследовать объект управления на управляемость;

4. Исследовать объект управления на наблюдаемость.


Выполнение работы

1

– 2

(– 1 9)

∫

ū ν Ä – Sxy

18 5

– 3 12

R

Уравнение объекта в векторной форме

ν = ν1 • u

ν2 – 2u


x = x1

x2


ν = 1 • u

– 2

S = ν – R

x = ⌠Sdt

R = 18 5

– 3 12

y = (– 1 9) • x = (– 1 9) • x1 = – x1 + 9x2

x2

dx/dt = SS = 1 • u – 18 5 • x

– 2 – 3 12


dx/dt = Ax + Du – уравнение объекта

Y = Cx + Du – уравнение выходных переменных

D = 0


u = u1 x = x1 y = y1

x2


A = 18 5 B = 1 C = (– 1 9)

– 3 12 – 2

Исследование объекта управления на устойчивость

det (A – pE) = 0

18 5 – p 0 = 18 – p 5

– 3 12 0 p – 3 12 – p

18 – p 5

– 3 12 – p = (18 – p) (12 – p) – 5 • (– 3) = 216 – 18p – 12p + p2 + 15 = p2 – 30p + 231

p2 – 30p + 231 = 0

p1 = (900 + √–24) / 2 = 15 + √6 j

p2 = (900 – √–24 ) / 2 = 15 – √6 j

Rep1 > 0

Rep2 > 0,

следовательно система неустойчива.

Исследование объекта управления на управляемость

dx/dt = Ax + Bu

Порядок n = 2

Матрица управляемости: R = (BAB)


A • B = 18 5 • 1 = 18 • 1 + 5 • (– 2) = 8

– 3 12 – 2 – 3 • 1 + 12 • (– 2) – 2


R = 1 8

– 2 – 27


1 8 = 1 • (–27) – 8 • (– 2) = – 27 + 16 = – 11≠ 0

– 2 – 27

Следовательно r =2 = n

Объект управляем.

Исследование на наблюдаемость


HT = C

CA


C • A = (– 1 9) • 18 5 = –1•18+9•(–3) –1•5+9•12 = (– 45 103)

– 3 12


HT = – 1 9

– 45 103

– 1 9 = – 103 + 405 = 302 ≠ 0, следовательно r = 2 = n

– 45 103

Система наблюдаема.

Похожие работы

  • Устойчивость линейных систем автоматического управления

    Реферат на тему: "Устойчивость линейных систем автоматического управления" 1. Общие понятия устойчивости Устойчивость – это свойство системы возвращаться в исходное состояние после вывода ее из состояния равновесия и прекращения действия возмущения. Устойчивость – это одно из основных требований, предъявляемых к системе.

  • Управление динамической системой

    Нахождение аналитического вида функций Mc(w), Mg(w,m) и передаточной функции для разомкнутой системы. Линеаризация и численное решение разомкнутой системы. Оценка управляемости и устойчивости системы. Амплитудная, фазовая, мнимая частотные характеристики.

  • Модернизация электронного термометра

    Теоретические основы методов расчета корректирующих цепей САУ и исследование их устойчивости. Особенности модернизации электронного термометра с использованием корректирующей цепи последовательного типа. Исследование устойчивости типовых звеньев САУ.

  • Методы поиска отказов

    Теоретические основы поиска, отказа - диагностирования, целью которого является определение места и при необходимости причины и вида отказа объекта. Особенности измерения диагностических признаков (проверки): время, масса оборудования, его стоимость.

  • Анализ динамических свойств системы автоматического управления заданной структурной схемы

    Анализ устойчивости системы автоматического управления (САУ) по критерию Найквиста. Исследование устойчивости САУ по амплитудно-фазочастотной характеристике АФЧХ и по логарифмическим характеристикам. Инструменты управления приборной следящей системы.

  • Анализ тестопригодности по методу Сamelot

    Процесс распространения информации о неисправности через устройства. Определение управляемости, наблюдаемости, наличие обратных связей и ветвления на выходе устройства. Определение тестопригодности для сходящихся путей равной и неравной длины узла.

  • Наблюдатель Люенбергера

    Непрерывная система с передаточной функцией. Оценка состояния объекта с помощью наблюдателя пониженного порядка. Расчет наблюдателя Люенбергера, оценивание вектора состояний. Решение задачи с использованием MatLab, построение графиков вектора состояния.

  • Устойчивость дискретных систем управления

    Основные понятия устойчивости дискретных систем. Критерий устойчивости Михайлова с использованием билинейного преобразования. Определение устойчивости дискретных систем в форме z-преобразования. Применение критериев устойчивости для дискретных систем.

  • Теория информационных процессов

    Система автоматического управления. Алгоритм модального формирования динамических свойств системы. Матрица линейных стационарных обратных связей на основе алгебраического уравнения типа Сильвестра. Математическая модель наблюдателя Люенбергера.

  • Синтез и построение системы управления динамическими объектами

    Синтез системы управления квазистационарным объектом. Математическая модель нестационарного динамического объекта. Передаточные функции звеньев системы управления. Построение желаемых логарифмических амплитудно-частотных и фазочастотных характеристик.