Название: Определение статистических данных производства продукции

Вид работы: контрольная работа

Рубрика: Экономика

Размер файла: 66.74 Kb

Скачать файл: referat.me-382755.docx

Краткое описание работы: Квадратичный коэффициент вариации. Средняя ошибка доли признака. Анализ ряда динамики абсолютного и среднего прироста младенческой смертности в Украине. Индекс себестоимости переменного и постоянного состава одноименной продукции по двум заводам.

Определение статистических данных производства продукции

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ

Контрольная работа по курсу

"Статистика"

Задача № 1

Определим величину интервала

I= (8,1-0,5): 4=7,6: 4=1,9

Количество заводов по группам.

№ группы	Группировка заводов		Среднегодовая стоимость		Валовая продукция в сопоставимых ценах, грн.		Уровень фондоотдачи (%)
	к-во шт.	№ №	всего	на завод	всего	на завод
1	5	1,8,12,13, 20	5,0	1,0	4,5	0,9	90
2	8	2,3,5,7,9,11,22,23,	26,9	3,3625	26,8	3,35	99,6
3	6	4,6,10,15,18,21	30,3	13,3	35	5,833	115,5
4	5	14,16,17, 19,24	34,8	6,96	34,5	6,9	99

Интервал для групп заводов:

1-я: 0,5…2,4

2-я: 2,4…4,3

3-я: 4,3…6,2

4-я: 6,2…8,1

Уровень фондоотдачи = (Валовая продукция / стоимость ОФ) * 100%

Выводы: с ростом стоимости основных фондов (ОФ) растет стоимость валовой продукции следовательно между этими показателями существует прямая зависимость. Уровень фондоотдачи не зависит от изменения стоимости ОФ и стоимости валовой продукции.

Задача № 2

Имеются данные по двум заводам, вырабатывающим однородную продукцию (табл.31).

Таблица 31

Номер завода	1998 год		1999 год
	Затраты времени на единицу продукции, ч	Изготовление продукции, шт.	Затраты времени на единицу продукции, ч	Затраты времени на всю продукцию, ч
1	2,0	150	1,9	380
2	3,0	250	3,0	840

Вычислите средние затраты времени на изготовление единицы продукции по двум заводам с 1998 по 1999 г.

Укажите, какой вид средней необходимо применять при вычислении этих показателей.

Решение.

Если в статистической совокупности дан признак Xi и его частота fi, то расчет ведется по формуле средней арифметической взвешенной:

(ч)

Если дан признак x_i , нет его частоты f_i , а дан объем M = x_i f_i распространения явления, тогда расчет ведем по формуле средней гармонической взвешенной:

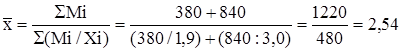(ч)

Вывод:

В среднем затраты времени на изготовление единицы продукции в 1998г. выше, чем в 1999г.

Задача 3

Для определения средней суммы вклада в сберегательных кассах района, имеющего 9000 вкладчиков, проведена 10% -я механическая выборка, результаты которой представлены в таблице.

Группы вкладов по размеру, грн. - xi	До 200	200-400	400-600	600-800	Св.800	Σ
Число вкладчиков - fi	80	100	200	370	150	900
Середина интервала	100	300	500	700	700
x - A=x' - 700	-600	-400	-200	0	+200
(X - A) / i	-3	-2	-1	0	1
( (X - A) / I) *f	-240	-200	-200	0	150	-490
( (X - A) / I) 2 *f	720	400	200	0	150	1470

Решение: для определения средней суммы вкладов способов моментов воспользуемся формулой:

= m₁ Δ*I+Ai

где: m₁ - момент первого порядка, x – варианта, i - величина интервала, f – частота, Δ - постоянная величина, на которую уменьшаются все значения признака.

m₁ = (Σ ( (X-A) / i)) *f) / Σf

= ( (Σ ( (X-A) / i*f) / Σf) *i+A

Находим середины интервалов

(200 + 400) / 2 = 300 - для закрытых интервалов;

Для открытых интервалов вторая граница достраивается:

(0 + 200) / 2 = 100

Величина интервала i = 200.

Наибольшая частота равна 370, следовательно А = 700.

В вариационных рядах с равными интервалами в качестве А принимается вариант с наибольшей частотой.

Число вкладчиков

f=900

m₁ = (-240-200-200+150) / 900=-0,544

=-0,544*200+700=591,2 грн.

Вывод: в среднем сумма вкладов составляет 591,2 грн.

Определим дисперсию способом моментов:

σ²² =i² * (m_{2 -} )

m₁ =-0.544; m₂ = (Σ ( (X-A) / i) ² *f) / Σf

m₂ =1470/900=1,63

σ² =200² * (1,63- (-0,544) ² ) =53362,56 среднеквадратичное отклонение:

=231 грн.

Соотношение среднеквадратичного отклонения к средней называют квадратичным коэффициентом вариации:

V= (σ/) *100%= (231/591,2) *100=39,07%

Предельная ошибка выборки средней вычисляется по формуле:

Δx=t*2/n, Δx=2* (грн)

где: n - выбранной совокупности, n=900, σ² – дисперсия, t - коэффициент доверия (табличное значение для вероятности 0,954 соответствует t=2).

Δx=2*15,4 (грн)

Т.о. с вероятностью 0,954 можно сказать, что средняя сумма вкладов в сберкассах района находится в пределах

591,2-15,4 ≤ x ≤ 591,2+15,4

575,8 ≤ x ≤ 606,4

Средняя ошибка доли признака. Доля признака в выборочной совокупности:

Р==20%, μ=

Nт=9000 интегральная совокупность, n=900 - выборочная совокупность

μ ==0,01265=1,3%

Δ=t*M=2*1,3=2,6%

20-6 ≤ ≤ 20+2,6 => 17,4 ≤ ≤ 22,6

Задача 4

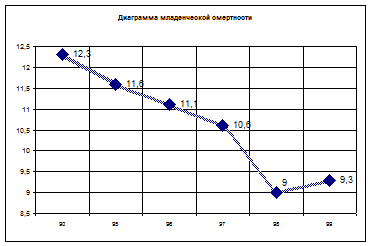
Имеются данные о младенческой смертности на Украине

Год	1990	1995	1996	1997	1998	1999
Умерло детей в возрасте до 1 года (всего), тыс. чел.	12,3	11,6	11,1	10,6	9,0	9,3

Для анализа ряда динамики исчислите:

1) абсолютный прирост, темпы роста и прироста (по годам и к базисному 1995 г), абсолютное содержание 1% прироста (полученные показатели представьте в виде таблицы);

2) среднегодовой темп роста и прироста младенческой смертности: а) с 1990 по 1996 годы; б) с 1995 по 1999 годы; в) с 1990 по 1999 годы. Изобразите исходные данные графически. Сделайте выводы.

Решение:

1. Абсолютный прирост (Δ_i ) определяется как разность между двумя уровнями динамического ряда и показывает, на сколько данный уровень ряда превышает уровень, принятый за базу сравнения Δ_i =y_i -y_баз , где y_i - уровень сравниваемого периода; y_баз - базисный уровень. При сравнении с переменной базой абсолютный прирост будет равен Δ_i =y_i -y_{i -1} , где y_i - уровень сравниваемого периода; y_{i -1} - предыдущий уровень. Темпы роста определяются как процентное отношение двух сравниваемых уровней:

При сравнении с базисом:

.

По годам:

.

Темп прироста показывает, на сколько процентов уровень данного периода больше (или меньше) базисного уровня.

По отношению к базисному:

;

по годам:

или можно вычислять так:

Тп=Тр- 100%.

Абсолютное содержание 1% прироста - сравнение темпа прироста с показателем абсолютного роста:

.

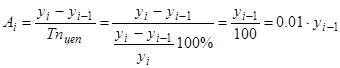2. Среднегодовая младенческая смертность вычисляется по формуле:

.

3. Среднегодовой абсолютный прирост вычисляется по формуле:

.

4. Базисный темп роста с помощью взаимосвязи цепных темпов роста вычисляется по формуле:

.

5. Среднегодовой темп роста вычисляется по формуле:

.

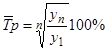Среднегодовой темп прироста вычисляется по формуле:

.

Рассчитанные данные представим в таблице

Год	Умерло, тыс. чел.	Абсол. прирост		Ср. год. темп роста		Ср. год. темп прироста		Аі
		цепн.	базисн.	цепн.	базисн.	цепн.	базисн.
1990	12,3	-	0,7	-	106,8	-	6,8	-
1995	11,6	0,7	0	94	100	-6	-	0,125
1996	11,1	0,5	0,5	102	102	2	2	0,12
1997	10,6	0,5	0,8	89	90,6	-11	-0,4	0,12
1998	9.0	1,6	0,8	89	80,3	-11	-19,7	0,11
1999	9,3	-0,3	-1,1	99	78,6	-1	-21,4	0,09

В качестве базисного берем 1995 г.

Среднегодовой темп роста
с 1990 по 1996	98,30
с 1995 по 1999	94,63
с 1990 по 1999	96,94
Среднегодовой темп прироста
с 1990 по 1996	-1,70
с 1995 по 1999	-5,37
с 1990 по 1999	-3,06

Задача 5

Реализация товаров на колхозном рынке характеризуется данными представленными в табл.5.

Таблица 5.

Наименование товара	Базисный период		Отчетный период
	Количество, тыс. кг.	Цена 1 кг., грн	Количество, тыс. грн.	Цена 1 кг., грн
Картофель	15,0	0,3	20	0,5
Мясо	3,0	3,5	4	5

Определите:

1) общий индекс физического объема продукции;

2) общий индекс цен и абсолютный размер экономии (перерасхода) от изменения цен;

3) на основании исчисленных индексов определить индекс товарооборота.

Решение.

Индекс представляет собой относительную величину, получаемую в результате сопоставления уровней сложных социально-экономических показателей во времени, в пространстве или с планом.

Индивидуальными называются индексы, характеризующие изменения только одного элемента совокупности.

Общий индекс отражает изменение по всей совокупности элементов сложного явления.

Стоимость - это качественный показатель.

Физический объем продукции - количественный показатель.

Общий индекс физического объема продукции вычисляется по формуле:

,

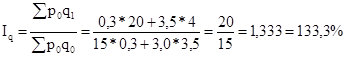где p₀ и р₁ - цена единицы товара соответственно в базисном и отчетном периодах;

q₀ и q_{1 -} количество (физический объем) товара соответственно в базисном и отчетном периодах.

Количество проданных товаров увеличилось на 33,3%.

Или в деньгах: 20 - 15 = 5,0 тыс. грн.

Общий индекс стоимости вычисляется по формуле:

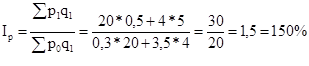
Следовательно, цены на данные товары в среднем увеличились на 50%.

Сумма сэкономленных или перерасходованных денег:

сумма возросла на 50%, следовательно, население в отчетном периоде на покупку данных товаров дополнительно израсходует: 30 - 20 = 10 тыс. грн.

Общий индекс товарооборота вычисляется по формуле:

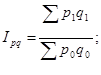
Товарооборот в среднем возрос на 100%.

Взаимосвязь индексов:

1,333 * 1,5 = 2,0

Задача 6

Имеются данные о выпуске одноименной продукции и её себестоимости по двум заводам

Завод	Производство продукции, тыс. шт.		Себестоимость 1 шт., грн.
	I квартал	II квартал	I квартал	II квартал
I	100	180	100	96
II	60	90	90	80

Вычислите индексы:

1) себестоимости переменного состава;

2) себестоимости постоянного состава;

3) структурных сдвигов. Поясните полученные результаты.

Решение.

Индекс себестоимости переменного состава вычисляется по формуле:

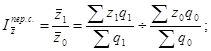
где z₀ и z_{1 -} себестоимость единицы продукции соответственно базисного и отчетного периодов;

q₀ и q_{1 -} количество (физический объем) продукции соответственно в базисном и отчетном периодах.

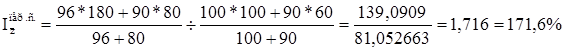
Индекс показывает, что средняя себестоимость по двум заводам повысилась на 71,6%, это повышение обусловлено изменением себестоимости продукции по каждому заводу и изменением структуры продукции (увеличением объема выпуска).

Выявим влияние каждого из этих факторов.

Индекс себестоимости постоянного состава вычисляется по формуле:

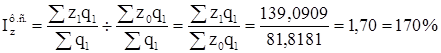
То есть себестоимость продукции по двум заводам в среднем возросла на 70%.

Индекс себестоимости структурных сдвигов вычисляется по формуле:

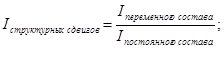
Или

Взаимосвязь индексов:

170*100,9=171,6

Вывод :

Индекс себестоимости переменного состава зависит от изменения уровня себестоимости и от изменения объема производства, т.е. средний прирост себестоимости составил 71,6%.

Индекс себестоимости постоянного состава показывает изменение себестоимости при фиксированном объеме производства, т.е. в среднем по заводам себестоимость повысилась на 71%. Индекс себестоимости переменного состава выше, чем индекс себестоимости постоянного состава, это свидетельствует о том, что произошли благоприятные структурные сдвиги. Индекс структурных сдвигов равен 1,009%, т.е. за счет изменения объемов производства по заводам средняя себестоимость повысилась на 0,9%.

Задача 7

Для изучения тесноты связи между выпуском валовой продукции на один завод (результативный признак Y) и оснащенностью заводов основными производственными фондами (факторный признак X) по данным задачи 1 вычислить коэффициент детерминации и эмпирическое корреляционное отношение.

Решение.

Показателем тесноты связи между факторами, является линейный коэффициент корреляции.

Линейный коэффициент корреляции вычислим по формуле:

.

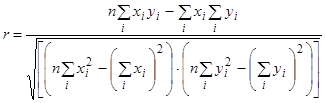Линейное уравнение регрессии имеет вид: y=bx-а.

Коэффициент детерминации показывает насколько вариация признака зависит от фактора, положенного в основу группировки и вычисляется по формуле:

где d² - внутригрупповая дисперсия;

s² - общая дисперсия.

Общая дисперсия характеризует вариацию признака, который зависит от всех условий в данной совокупности.

Межгрупповая дисперсия отражает вариацию изучаемого признака, которая возникает под влиянием фактора, положенного в основу группировки и рассчитывается по формуле:

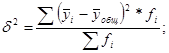
где среднее значение по отдельным группам;

f_i - частота каждой группы.

Средняя из внутригрупповых дисперсия:

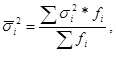
где - дисперсия каждой группы.

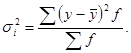
Эмпирическое корреляционное отношение рассчитывается по формуле:

Все расчетные данные приведены в таблице 7.

Таблица 7

№ завода	Среднегодовая стоимость ОФ, млн. грн. (X)	Валовая продукция в сопоставимых ценах, грн. (Y)	X^2	Y^2	XY
1	1,6	1,5	2,56	2,25	2,55
2	3,9	4,2	15,21	17,64	17,16
3	3,3	4,5	10,89	20,25	15,75
4	4,9	4,4	24,01	19,36	22,05
5	3,0	2,0	9	4	6,4
6	5,1	4,2	26,01	17,64	22,44
7	3,1	4,0	9,61	16	13,2
8	0,5	0,4	0,25	0,16	0,1
9	3,1	3,6	9,61	12,96	11,52
10	5,6	7,9	31,36	62,41	43,68
11	3,5	3,0	12,25	9	10,8
12	0,9	0,6	0,81	0,36	0,63
13	1,0	1,1	1	1,21	1,32
14	7,0	7,5	49	56,25	53,9
15	4,5	5,6	20,25	31,36	25,76
16	8,1	7,6	65,61	57,76	63,18
17	6,3	6,0	39,69	36	38,4
18	5,5	8,4	30,25	70,56	46,75
19	6,6	6,5	43,56	42,25	43,55
20	1,0	0,9	1	0,81	0,8
21	4,7	4,5	22,09	20,25	21,6
22	2,7	2,3	7,29	5,29	6,75
23	2,9	3,2	8,41	10,24	8,96
24	6,8	6,9	46,24	47,61	46,24
Итого	95,6	100,8	485,96	561,62	523,49
Среднее	3,824	4,032	19,4384	22,4648	21,81

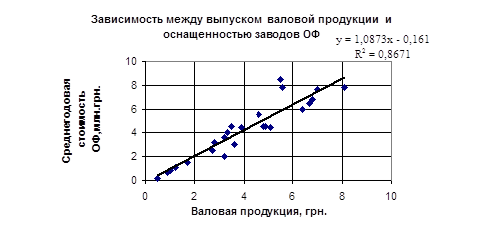
Подставив вычисленные значения в формулу, получим:

Коэффициент детерминации h² = 0,87.

Эмпирическое корреляционное отношение имеет вид: у = 1,0873х - 0,161.

Линейный коэффициент корреляции r = 0,93.

a=0,161b=1,0873

Так как значение коэффициента корреляции близко к единице, то между выпуском валовой продукции и оснащенностью заводов основными производственными фондами есть тесная зависимость.

b - коэффициент регрессии, т.к b > 0, то связь прямая.

Список использованной литературы

1. 1. Адамов В.Е. Факторный индексный анализ. - М.: Статистика, 1997.

2. 2. Елисеева И.И., Юзбашев М.М. Общая теория статистики: Учебник. - М.: Финансы и статистика, 2004.

3. 3. Ефимова М.Р., Рябцев В.Ф. Общая теория статистики: Учебник. М.: Финансы и статистика, 1999.