Название: Динаміка економічних показників. Структура зовнішньо-торгівельного обороту підриємства

Вид работы: контрольная работа

Рубрика: Экономика

Размер файла: 254 Kb

Скачать файл: referat.me-385545.docx

Краткое описание работы: Складання комбінаційного розподілу виробничих ділянок. Визначення відносних величин, які характеризують: динаміку показників; структуру зовнішньо-торгівельного обороту та структурні зрушення; інтенсивність зовнішньоекономічної діяльності за кожен рік.

Динаміка економічних показників. Структура зовнішньо-торгівельного обороту підриємства

СТАТИСТИКА

КОНТРОЛЬНА РОБОТА

Рішення задач з економічної статистики (варіант №9)

Зміст

1. Завдання №1 (варіант №9)

2. Завдання №2 (варіант №9)

3. Завдання №3 (варіант №9)

4. Завдання №4 (варіант №9)

5. Завдання №5 (варіант №9)

Список використаної літератури

1. Завдання №1 (варіант №9)

За наведеними даними про порушення технологічної дисципліни та втрати від браку продукції на 22 виробничих ділянках складіть комбінаційний розподіл виробничих ділянок за цими ознаками, утворивши по три групи з рівними інтервалами (за результатами групування зробіть висновок про наявність та напрямок зв’язку між ознаками).

№ ділянки п/п	Процент порушень технологічної дисципліни, %	Втрати від браку продукції, тис.гр.од.	№ ділянки п/п	Процент порушень технологічної дисципліни, %	Втрати від браку продукції, тис.гр.од.
1	1,2	1,0	12	1,7	1,5
2	2,0	1,6	13	2,1	1,7
3	1,4	1,2	14	1,3	1,4
4	1,9	1,5	15	2,0	1,8
5	1,6	1,4	16	2,3	1,6
6	2,4	1,9	17	2,5	2,0
7	1,8	1,4	18	2,7	2,1
8	2,6	2,1	19	2,6	2,0
9	2,0	1,7	20	1,7	1,4
10	1,5	1,2	21	1,5	1,3
11	1,2	0,9	22	2,1	1,6

Результати групувань викладіть в формі статистичних таблиць, проаналізуйте їх.

Рішення

1. Для рішення завдання виділимо факторну ознаку Х процент порушень технологічної дисципліни (%) на виробничій ділянці та результативну ознаку Y втрати від браку продукції (тис.гр.од.) на виробничій ділянці [6]. Кількість виробничих ділянок n = 22.

В табл.1.1 наведені ранжована по факторній ознаці Х [1] вибірка значень для 22 виробничих ділянок.

Таблиця 1.1 Ранжована по зростанню факторної ознаки Х вибірка даних

№ ранжованих ділянок п/п (n)	№ вихідних ділянок п/п	Ранжований ряд проценту порушень технологічної дисципліни, % (Х)	Втрати від браку продукції, тис.гр.од. (Y)
1	1	1,2	1
2	11	1,2	0,9
3	14	1,3	1,4
4	3	1,4	1,2
5	10	1,5	1,2
6	21	1,5	1,3
7	5	1,6	1,4
8	12	1,7	1,5
9	20	1,7	1,4
10	7	1,8	1,4
11	4	1,9	1,5
12	2	2	1,6
13	9	2	1,7
14	15	2	1,8
15	13	2,1	1,7
16	22	2,1	1,6
17	16	2,3	1,6
18	6	2,4	1,9
19	17	2,5	2
20	8	2,6	2,1
21	19	2,6	2
22	18	2,7	2,1

Згідно з умовами задачі розбиваємо ранжовану за факторною ознакою вибірку на 3 рівних інтервала:

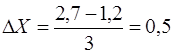
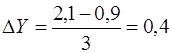
В таблиці 1.2 наведені інтервали факторної та результативної вибірок на 3 інтервалах та частоти значень факторних та результативних рядів, які згідно таблиці 1.1 розподіляються по інтервалам.

Таблиця 1.2 Частотний розподіл ранжованих рядів по інтервалах вибірок

Факторна ознака
Інтервал процентів порушень технологічної дисципліни X, %	Кількість виробничих участків в інтервалі (частота f)	Середина інтервалу (варіанти), x/	Варіанти зважені на частоти, x/ f	Кумулятивні частоти, S(x)
1,20 1,69	7	1,45	10,15	7
1,70 2,20	9	1,95	17,55	16
2,21 2,70	6	2,45	14,7	22
Разом	22		42,4

Результативна ознака
Інтервал втрат від браку продукції, тис.гр.од.	Кількість виробничих участків в інтервалі (частота f)	Середина інтервалу (варіанти), y/	Варіанти зважені на частоти, y/ f	Кумулятивні частоти, S(y)
0,901,29	4	1,1	4,4	4
1,301,70	12	1,5	18	16
1,712,10	6	1,9	11,4	22
Разом	22		33,8

2. Розраховуємо основні показники інтервальних рядів [12]:

середнє значення;

середньоквадратичне відхилення;

варіацію.

Середня величина факторної ознаки згідно з даними таблиці 1.2 розраховується як

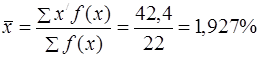(1.1)

Середня величина результативної ознаки згідно з даними таблиці 1.2 розраховується як

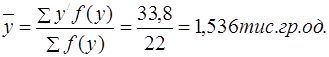(1.2)

Ступінь варіації об’єктивно відображає показник середнього квадрату відхилення (дисперсія). Його обчислюють як середню арифметичну з суми квадратів відхилень окремих варіантів від їх середньої за формулою [12]:

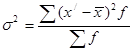(1.3)

Корінь квадратний із середнього квадрату відхилень варіантів від їх середньої (тобто дисперсії) називається середнім квадратичним відхиленням [12]:

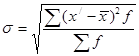(1.4)

Середньоквадратичне відхилення для факторної та результативної ознак, з врахуванням даних табл.1.1, розраховується як:

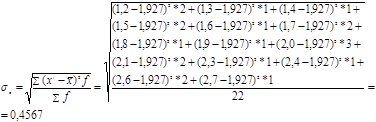
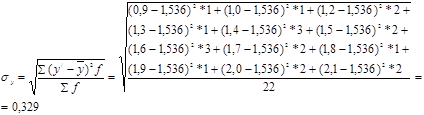
Якщо порівняти середнє квадратичне відхилення з середньою величиною, то і буде одержана ця стандартна величина. Одержаний відносний показник називається коефіцієнтом варіації [12]:

(1.5)

де середнє арифметичне інтервального ряду розподілу, f – частота.

Коефіцієнт варіації є в певній мірі критерієм типовості середньої, при коефіцієнті варіації до 33% констатують, що середня величина в достатній мірі характеризує вибірку. Якщо коефіцієнт дуже великий, то це означає, що середня характеризує сукупність за ознакою, яка суттєво змінюється у окремих одиниць [12].

Коефіцієнти варіації для факторної та результативної ознак виборки дорівнюватимуть:

Таблиця 1.3 Проміжні розрахунки середньоквадратичних відхилень та коефіцієнта кореляції вибірок

№ ранжованих ділянок п/п	№ вихідних ділянок п/п	Ранжований ряд проценту порушень технологічної дисципліни, %(X)	Втрати від браку продукції, тис.гр.од. (Y)	(ХХср)2	(YYср)2	(ХХср)* (YYср)
1	1	1,2	1	0,528529	0,287296	0,389672
2	11	1,2	0,9	0,528529	0,404496	0,462372
3	14	1,3	1,4	0,393129	0,018496	0,085272
4	3	1,4	1,2	0,277729	0,112896	0,177072
5	10	1,5	1,2	0,182329	0,112896	0,143472
6	21	1,5	1,3	0,182329	0,055696	0,100772
7	5	1,6	1,4	0,106929	0,018496	0,044472
8	12	1,7	1,5	0,051529	0,001296	0,008172
9	20	1,7	1,4	0,051529	0,018496	0,030872
10	7	1,8	1,4	0,016129	0,018496	0,017272
11	4	1,9	1,5	0,000729	0,001296	0,000972
12	2	2	1,6	0,005329	0,004096	0,004672
13	9	2	1,7	0,005329	0,026896	0,011972
14	15	2	1,8	0,005329	0,069696	0,019272
15	13	2,1	1,7	0,029929	0,026896	0,028372
16	22	2,1	1,6	0,029929	0,004096	0,011072
17	16	2,3	1,6	0,139129	0,004096	0,023872
18	6	2,4	1,9	0,223729	0,132496	0,172172
19	17	2,5	2	0,328329	0,215296	0,265872
20	8	2,6	2,1	0,452929	0,318096	0,379572
21	19	2,6	2	0,452929	0,215296	0,312272
22	18	2,7	2,1	0,597529	0,318096	0,435972
			Сума	0,45675	0,32924	3,12548

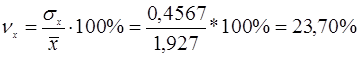
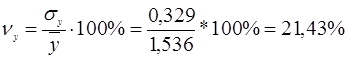
Оскільки величини варіації менше 33%, вважаємо отримані характеристики середніх величин та середньоквадратичних відхилень суттєвими.

Лінійний коефіцієнт кореляції між факторною X та результативною Y ознакою обчислюється за формулою [10] (з врахуванням даних проміжних розрахунків, наведених в табл.1.3):

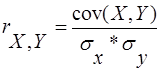(1.6)

де 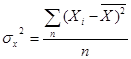дисперсія вибірки величин Х; (1.7)

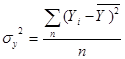дисперсія вибірки величин Y; (1.8)

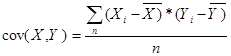коваріація виборок X,Y (1.8)

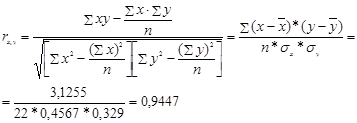(1.9)

Лінійний коефіцієнт кореляції чим ближче до 1, тим тісніше зв’язок. Знак коефіцієнта вказує напрямок зв’язку: знак “+” відповідає прямій залежності, знак ““ – оберненій залежності [10].

Таким чином, між факторною ознакою Х та результативною ознакою Y вихідної вибірки задачі існує пряма залежність дуже тісного зв’язку.

На рис.1.1 наведені результати побудування в „електронних таблицях” Excel2000 лінійної регресії між Y та X, що підтверджує тісний прямий зв’язок, характеризуємий високим значенням індекса детермінації R² >0,75 .

Коефіцієнт детермінації визначається як відношення сум відхилення аналітичних значень Yx від середнього значення ряда вибірки до сум відхилення фактичних значень Yi від середнього значення ряда вибірки наступним чином [10]:

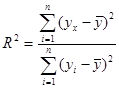(1.10)

Щільність зв’язку оцінюється індексом детермінації: R=, проте інтерпретується тільки R² . Якщо коефіцієнт детермінації більше 0,75 , то більше 75% варіації залежної величини Y пояснюється варіацією незалежного параметра кореляції X і зв’язок є щільним [10].

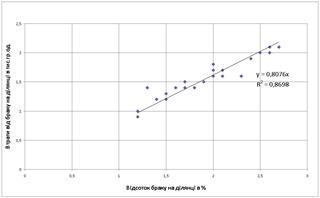
Рис.1.1. – Кореляційно-регресійна лінійна залежність між результативною Y та факторною X ознаками досліджуємої вибірки

2. Завдання №2 (варіант №9)

За наведеними даними визначте відносні величини, які б характеризували:

а) динаміку показників;

б) структуру зовнішньо-торгівельного обороту та структурні зрушення;

в) інтенсивність зовнішньоекономічної діяльності за кожен рік;

г) на основі співвідношення індексів цін експорту та імпорту дайте оцінку умов торгівлі.

Зробіть висновки.

Рік	ВНП, млрд. гр.од.	Оборот зовнішньої торгівлі, млрд.гр.од.	У т.ч. експорт та імпорт, млрд.гр.од.		Індекси цін, %
			товарів	послуг	експорту	імпорту
Минулий	560	140	91	49	102,0	107,1
Поточний	726	220	132	88	106,6	103,0

Рішення

1. Рішення задачі оцінки динаміки росту показників зовнішньоекономічної діяльності виконаємо з застосуванням апарату індивідуальних та загальних індексів [14].

Індексом у статистиці називається відносний показник, який характеризує зміну рівня якогось суспільного явища з часом або його співвідношення у просторі.

Прийнято розрізняти дві категорії індексів: індивідуальні та загальні. Індекс, який характеризує співвідношення величин окремого явища, називається індивідуальним, а індекс, котрий характеризує співвідношення рівнів усього явища в цілому або його частин, що складаються з кількох окремих елементів, які безпосередньо не піддаються підсумовуванню, загальним.

Статистичний індекс – це узагальнюючий показник, який виражає співвідношення величин складного економічного явища, що складається з елементів безпосередньо несумірних. У статистиці розрізняють декілька вдів індексів, в основу класифікації яких покладені різні ознаки [14]:

- характер об'єкта дослідження,

- ступінь охоплення одиниць сукупності,

- база порівняння,

- вид зрівнюваних величин.

Індивідуальні індекси дають порівняльну характеристику окремих елементів складного явища і мають форму відношення певного показника у базисному (0) та звітному (1) періодах [14]:

(2.1)

Загальний індекс є агрегатуваннням індивідуальних індексів і характеризує зміну сукупностей, до якої входять різнорідні елементи . Так загальна формула агрегатного індексу сукупності явищ у базисному (0) та звітному (1) періоді має наступний вираз(для вартісних економічних явищ , які характеризуються обсягами (q) та ціною (р) одиниці обсягу):

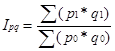(2.2)

Для характеристики економічних явищ загальний агрегатний індекс (2.2) розбивають на два індекси :

- загальний індекс фізичного обсягу вартісного явища (при умові незмінних цін р у базисному та звітному періодах):

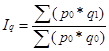(2.3)

- загальний індекс цін вартісного явища (при умові незмінного обсягу q у базисному та звітному періодах):

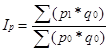(2.4)

Для характеризування структурних зрушень середніх величин в вартісних економічних явищах застосовують індекси змінного складу, індекси постійного складу та індекси структурних зрушень, які формують систему взаємопов'язаних індексів [14]:

- для змінного індексу цін (відношення середніх рівнів у базисному та звітному періодах):

(2.5)

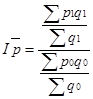(2.6)

де індекс цін постійного складу Ipz дорівнює :

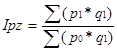(2.7)

а індекс цін за рахунок структурних зрушень Id дорівнює :

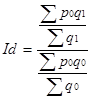(2.8)

2. Розраховуємо показники динаміки зміни параметрів зовнішньоекономічної торгівлі як індивідуальні індекси рівнів ВНП та зовнішньо-торгівельного обороту у поточному році (1) відносно минулого (0 – базового) року:

а) Індивідуальний індекс росту вартості ВНП дорівнює:

б) Індивідуальний індекс росту вартості обороту зовнішньоекономічної торгівлі (сума експорту та імпорту) дорівнює:

Таким чином, індекс росту вартості обороту зовнішньоекономічної торгівлі у поточному році вище індексу росту вартості ВНП в:

тобто в країні зростає обсяг зовнішньоекономічного сектору.

в) Індивідуальний індекс росту вартості обороту зовнішньоекономічної торгівлі товарами(сума експорту та імпорту) дорівнює:

г) Індивідуальний індекс росту вартості обороту зовнішньоекономічної торгівлі послугами(сума експорту та імпорту) дорівнює:

Таким чином, індекс росту вартості обороту зовнішньоекономічної торгівлі послугами у поточному році вище індексу росту вартості обороту зовнішньоекономічної торгівлі товарами в:

3. Структура зовнішньо-торгівельного обороту у базовому (0) та поточному роках розраховується як:

а) базовий (минулий рік):

питома вага зовнішньо-торгівельного обороту товарами становить

питома вага зовнішньо-торгівельного обороту послугами становить

б) поточний рік:

питома вага зовнішньо-торгівельного обороту товарами становить

питома вага зовнішньо-торгівельного обороту послугами становить

Таким чином, структурні зрушення в складі зовнішньої торгівлі у поточному році відносно базового(минулого) року характеризуються:

- зниженням на 5% питомої ваги торгівлі товарами ;

- підвищенням на 5% питомої ваги торгівлі послугами.

4. Інтенсивність зовнішньо-торгівельного обороту у базовому (0) та поточному(1) роках розраховується як відношення вартості обсягу зовнішньо-торгівельного обороту до вартості обсягів ВНП:

а) базовий (минулий рік):

б) поточний рік:

Таким чином, інтенсивність зовнішньої торгівлі в державі зросла на 5,3% від вартості обсягу ВНП держави.

5. Аналіз співвідношення індексів цін експорту та імпорту показує, що:

а) Індивідуальний темп росту індексу цін експорту дорівнює:

б) Індивідуальний темп росту індексу цін імпорту дорівнює:

Таким чином, темп росту індексу цін експорту зовнішньоекономічної торгівлі у поточному році вище темпу росту індексу цін імпорту зовнішньоекономічної торгівлі в:

тобто зовнішня торгівля є вигідною для держави.

3. Завдання №3 (варіант №9)

Є наступні дані вибіркового обстеження студентів одного з вузів:

Затрати часу на дорогу до інституту в год.	Число студентів , % до підсумку
До 0,5	7
0,5 – 1,0	18
1,0 – 1,5	32
1,5 – 2,0	37
Більше 2,0	6
Разом	100

Розрахуйте абсолютні та відносні показники варіації

Рішення

1. На рис.3.1 наведений графічний вигляд вихідної інтервальної статистичної вибірки (інтервальний варіаційний ряд) у вигляді гістограми.

2. Для інтервального ряду показник центру розподілу – середнє значення ряду розраховується за формулою [9]:

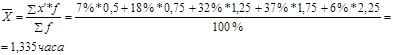(3.1)

де f – частота на інтервалі;

x’ – середина кожного інтервалу інтервальної вибірки;

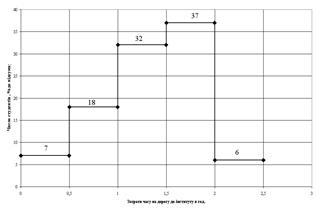
Рис.3.1. Гістограма вихідної інтервальної статистичної вибірки задачі

3. Показники варіації вибірки характеризуються:

абсолютним значення s середньоквадратичного відхилення від середнього рівня вибірки:

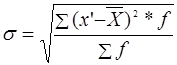(3.2)

- відносним рівнем варіації відношенням середньоквадратичного відхилення до середнього рівня вибірки:

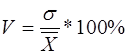(3.3)

Для розрахунку варіації складається наступна допоміжна таблиця 3.1

Таблиця 3.1 Результати допоміжних розрахунків для розрахунку показників варіації вибірки

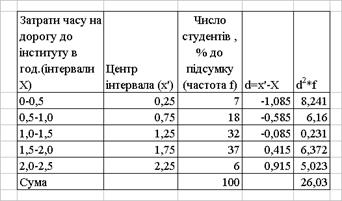
Абсолютне значення варіації вибірки дорівнює:

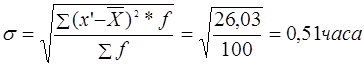
Відносне значення варіації вибірки дорівнює:

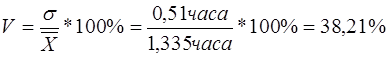
4. Завдання №4 (варіант №9)

Виробництво продуктів землеробства в регіоні характеризується наступними даними, млн.т.:

Рік	Льноволокно, млн..т.
1984	486
1985	456
1986	443
1987	402
1988	478
1989	509
1990	480
1991	384
1992	311
1993	284
1994	263
1995	414
1996	471
1997	478

Для вивчення загальної тенденції виробництва продукті землеробства зробіть:

а) згладжування рівнів рядів динаміки за допомогою тричленної ковзної середньої;

б) аналітичне вирівнювання.

Виразіть загальну тенденцію розвитку кожного виду продуктів землеробства за 1984 – 1997 рр. відповідними математичними рівняннями. Визначте вирівняні (теоретичні) рівні рядів динаміки і нанесіть їх на графік з фактичними даними. Зробіть висновки за результатами розрахунків.

Рішення

1. Для обробки ряду динаміки з метою зменшення коливань його рівнів використовується метод рухомої середньої [9]. Суть цього методу полягає у тому, що первинний ряд динаміки замінюється рядом середніх значень, підрахованих на основі рухомих сум. Рухома сума визначається шляхом додавання рівнів ряду, включених в інтервал вирівнювання (переважно це 3, 5, 7 рівнів).

Головним недоліком даного методу є те, що вирівняний ряд стає коротшим від вихідного за рахунок втрати рівнів на початку та в кінці ряду.

Рівняння тричленної ковзної середньої наступне ( перша та остання точка фактичного ряду динаміки не осереднюється) [9]:

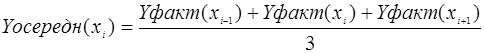(4.1)

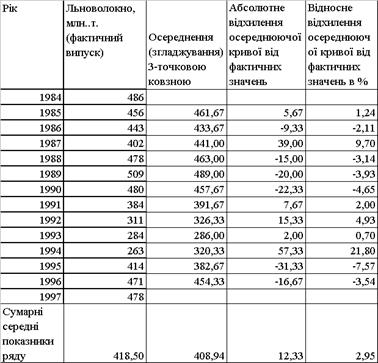
В табл..4.1 та на рис.4.1 наведені результати розрахунків осереднених значень вихідного ряду динаміки, заданого в завданні.

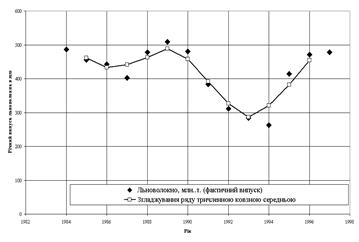
Рис.4.1. Результати розрахунку осереднення ряду тричленною ковзною

Таблиця 4.1 Результати розрахунку осереднення тричленною ковзною

2. Найбільш ефективним методом виявлення тенденції динаміки є аналітичне вирівнювання. Його суть полягає у тому, що вихідний ряд динаміки описують рівнянням тренду, яке розглядається як аналітичний вираз загальної тенденції зміни у часі (тренду). На практиці найчастіше використовують наступні рівняння тренду:

— лінійне
— параболічне
— показникове
— степеневе
— гіперболічне

Виконаємо аналітичне вирівнювання на прикладі лінійного рівняння тренду.

Одновимірна лінійна регресійна модель представляється як [9]:

, (2.1)

де – постійна складова (початок відліку);

– коефіцієнт регресії;

– відхилення фактичних значень доходу від оцінки (математичного сподівання) середньої величини доходу в ітий період.

Існують різні способи оцінювання параметрів регресії. Найпростішим, найуніверсальнішим є метод найменших квадратів [2]. За цим методом параметри визначаються виходячи з умови, що найкраще наближення, яке мають забезпечувати параметри регресії, досягається, коли сума квадратів різниць між фактичними значеннями прогнозує мого параметра та його оцінками є мінімальною, що можна записати як

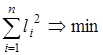. (2.2)

За методом найменших квадратів параметри регресії і є розв’язком системи двох нормальних рівнянь [9]:

При використанні прямолінійного тренду параметри і можуть бути знайдені шляхом рішення системи нормальних рівнянь

(2.3)

або по формулах

(2.4)

Таблиця 4.2 Розрахунки сум для розрахунку коефіцієнтів а₀ та а₁ лінійної регресії

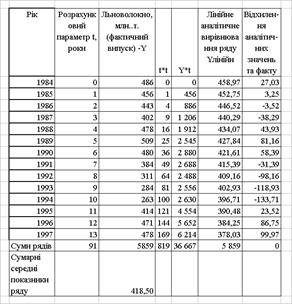
Таким чином, враховуючи розрахункові дані ряду динаміки в табл.4.2, коефіцієнти аналітичного рівняння лінійної регресії розраховуються як:

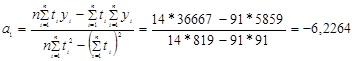
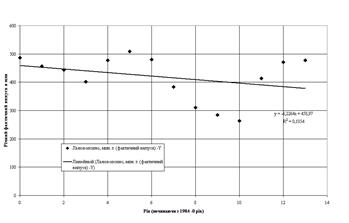
Рис.4.2. Аналітичне вирівнювання ряду лінійним трендом

Середньоквадратична помилка регресії, знаходиться за формулою

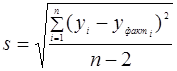, (2.5)

Коефіцієнт детермінації для даної моделі

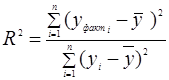(2.6)

повинен дорівнювати: >0,75 – сильний кореляційний зв’зок, 0,36>>0,75 кореляційний зв’язок середньої щільності; <0,36 кореляційній зв’язок низької щільності [10].

Як показують дані, наведені на рис.4.2, коефіцієнт детермінації для побудованого аналітичного лінійного тренду становить =0,1054 <0,36 тобто кореляційній зв’язок фактичних значень та аналітичного лінійного тренду є низької щільності.

Як показує спільний аналіз даних таблиць 4.1 та 4.2, а також графіків рис.4.1 та 4.2:

сума абсолютних відхилень кривої осереднення ряду тричленною ковзною становить 12,33;

сума абсолютних відхилень кривої аналітичного вирівнювання ряду лінійним трендом становить 0;

дисперсія відхилень кривої осереднення ряду тричленною ковзною від фактичних даних становить S² =634;

сума абсолютних відхилень кривої аналітичного вирівнювання ряду лінійним трендом від фактичних даних становить S² =5347;

Таким чином, вирівнювання ряду осереднюючою тричленою ковзною має кращі показники по мінімуму відхилень від фактичної кривої , але має зміщену середню оцінку, що пов’язано з алгоритмом розрахунку та неможливістю осереднення першої та останньої точки ряду.

На рис.4.3 – 4.4 за допомогою „електронних таблиць” Excel2000 побудовані аналітичні вирівнювання заданого ряду динаміки поліноміальними трендами 2 та 4 ступеню.

Як показують дані, наведені на рис.4.3, коефіцієнт детермінації для побудованого аналітичного параболічного тренду є вищим, ніж у лінійного тренду, та становить =0,243654 <0,36 тобто кореляційній зв’язок фактичних значень та аналітичного параболічного тренду також є низької щільності.

Як показують дані, наведені на рис.4.4, коефіцієнт детермінації для побудованого аналітичного тренду поліномом 4 ступеню є значно вищим, ніж у лінійного тренду, та становить =0,6024 (0,36>>0,75) тобто кореляційній зв’язок фактичних значень та аналітичного тренду полінома 4 ступеня є середньої щільності.

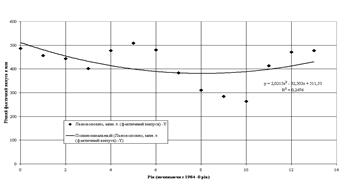
Рис.4.3. Аналітична вирівнювання ряду параболічним трендом за допомогою “електронних таблиць” Excel2000

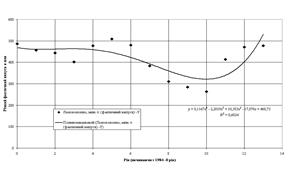
Рис.4.4. Аналітичне вирівнювання ряду поліномом (трендом) 4ступеня за допомогою “електронних таблиць” Excel2000

5. Завдання №5 (варіант №9)

Залежність скорочення робітників від місця роботи досліджувалася в ході соціологічного опитування 200 респондентів, результати якого представлені в наступній таблиці:

Думки респондентів	Робітники		Разом
	Державні підприємства	кооперативи
Дуже ймовірно	55	48	103
Практично неможливо	45	52	97
Разом	100	100	200

Визначте коефіцієнти асоціації і контингенції. Проаналізуйте отримані результати.

Рішення

Для аналізу взаємозв'язку між атрибутивними ознаками будуються спеціальні таблиці, що мають назву таблиць співзалежності. В тому випадку, коли утворюються по дві групи за факторною та результативною ознаками, або коли вони є альтернативними, для оцінки тісноти зв'язку визначають коефіцієнти асоціації Ка та контингенції Кк за формулами [3]:

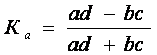(5.1)

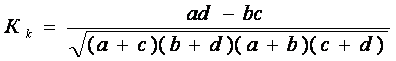(5.2)

Якщо модуль коефіцієнта асоціації (5.1) наближується до 1,0

то існує сильний зв'язок між групами ознак;

Якщо модуль коефіцієнта контингенції (5.2) наближується до 0,5

то існує сильний зв'язок між групами ознак;

Для розрахунку названих коефіцієнтів використовують так звані тетрахорічні таблиці, що показують розподіл одиниць за факторною та результативною ознаками [3].

Таблиця 5.1 Тетрахорічна таблиця для вихідних даних завдання

Результативна ознака (у) – „Думки респондентів”	Факторна ознака (х) – (Респонденти – робітники)
	х1 („Державні підприємства”)	х2 („Кооперативи”)	Разом
у1 („Дуже ймовірно”)	А = 55	B = 48	(a+b) =103
У2 („Майже неймовірно”)	С = 45	D = 52	(c+d) =97
Разом	(а+с) =100	(b+d) =100	(n) =200

Визначимо коефіцієнти асоціації та контингенції за даними таблиці 5.1:

Отже, за показником коефіцієнта асоціації Ка між Х та Y існує дуже слабкий прямий зв'язок.

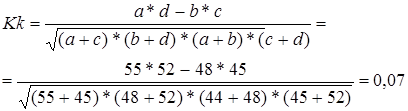
Отже, за показником коефіцієнта контингенції Кк також між Х та Y існує дуже слабкий прямий зв'язок.

Список використаної літератури

1. Ефимова М.Р., Ганченко О.И., Петрова Е.В. Практикум по общей теории статистики. М: Финансы и статистика, 2000. 280 c.

2. Ефимова М.Р., Петрова Е.В., Румянцев В.Н. и др. Общая теория статистики: Учебник. – М: ИнфраМ, 1998. – 436 c.

3. Єріна А.М. Теорія статистики : практикум / А. М. Єріна, З. О. Пальян. – 6те вид., стер. – К. : Знання, 2008. – 255 с.

4. Кармелюк Г. І. Теорія ймовірностей та математична статистика : посібник з розв’язування задач : навч. посібник / Г. І. Кармелюк. – К. : Центр учбової літератури, 2007. – 576 с.

5. Математика для економістів: теорія та застосування : підручник / В. П. Лавренчук [та ін.]. – К. : Кондор, 2007. – 596 с.

6. Мармоза А.Т. Практикум з теорії статистики : навч. посібник / А. Т. Мармоза. 3тє вид., виправл. К. : Ельга : НікаЦентр, 2007. 348 с.

7. Общая теория статистики. Статистическая методология в изучении коммерческой деятельности : учебник / под ред. О. Э. Башиной, А. А Спирина. 5е изд., перераб. и доп. М. : Финансы и статистика, 2007. 440 с. [

8. Орленко Н. С. Інформаційні системи і технології в статистиці : навчальнометодичний посібник для самост. вивчення дисципліни/ Н. С. Орленко ; Мво освіти і науки України, Держ. вищ. навч. заклад "Київський нац. екон. унт ім. В. Гетьмана". – К. : КНЕУ, 2008. – 282 с.

9. Практикум по эконометрике : учеб. пособие / И. И. Елисеева [и др.] ; под ред. И. И. Елисеевой. – 2е изд., перераб. и доп. – М. : Финансы и статистика, 2006. – 344 с.

10. Сеньо П. С. Теорія ймовірностей та математична статистика : підручник / П. С. Сеньо. – 2ге вид., переробл. і доповн. – К. : Знання, 2007. – 557 с.

11. Слюсарчук П. В. Теорія ймовірностей та математична статистика : підручник / П. В. Слюсарчук. – Ужгород : Карпати, 2005. – 183 с.

12. Статистика финансов : учебник / под ред. М. Г. Назарова. – 3е изд., испр. – М. : ОмегаЛ, 2007. – 461 с.

13. Статистика Конспект лекцій, Тернопіль, 2006р. – http;\ www.kneu.kiev.ua – Освітній Інтернетсайт Киівського національного економічного університету, 2008

14. Фінансовобанківська статистика : навч. посібник/ П. Г. Вашків [та ін.]. – К. : Либідь, 2007. – 512 с.