Название: Изучение норм расхода сырья

Вид работы: контрольная работа

Рубрика: Экономика

Размер файла: 268.67 Kb

Скачать файл: referat.me-395714.docx

Краткое описание работы: Вариант 5 Задача 1 В целях изучения норм расхода сырья проведена 1 процентная механическая выборка, в результате которой получено следующее распределение изделий по весу:

Изучение норм расхода сырья

Вариант 5

Задача 1

В целях изучения норм расхода сырья проведена 1 процентная механическая выборка, в результате которой получено следующее распределение изделий по весу:

Вес изделия, г.	Число изделий, шт.
До 2000	4
2000-2050	15
2050-2100	55
2100-2150	20
Свыше 2150	6
ИТОГО:	100

Известно также, что к стандартной продукции относятся изделия весом от 2000г. до 2150г. По данным обследования определите:

1) средний вес изделий;

2) моду и медиану;

3) размах вариаций;

4) среднее линейное отклонение;

5) дисперсию;

6) среднеквадратическое отклонение;

7) коэффициент вариации, оцените однородность совокупности;

8) с вероятностью 0,997 возможные пределы среднего веса изделия во всей партии изделий;

9) с вероятностью 0,954 возможные пределы удельного веса стандартной продукции по всей партии изделий.

Сделать выводы.

1) середина интервала

нижняя граница интервала

верхняя граница интервала

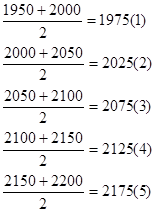
Средний вес изделий находим по формуле средней арифметической взвешенной:

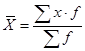
-варианты признаков

-частота

Средний вес изделий равен 2052г.

2) =

где - нижняя граница модального интервала

- величина модального интервала

- частота модального интервала

- частота интервала, предшествующего модальному

- частота интервала, следующего за модальным

=2050+50

=+

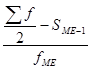
где -нижняя граница медианного интервала

-величина медианного интервала

-полусумма частот ряда

- сумма накопленных частот, предшествующих медианному интервалу

- частота медианного интервала

=2050+50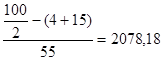

Итак, мода равна 2076,6, медиана 2078,18

3) -

где -максимальное значение признака

- минимальное значение признака

R= 55-4=51

4) =

=

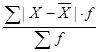
5) Ơ=

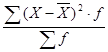
Ơ=

Дисперсия равна 5198264,95

6) Ơ=

Ơ==2279,97

Среднеквадратическое отклонение равно 2279,97

7) V=

V=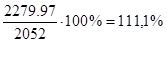

V=. 100% V= %

V< 33%, следовательно выборка однородна

8) Рассчитаем возможные пределы среднего веса изделия во всей партии изделий с вероятностью 0,997

2052

9) Рассчитаем возможные пределы удельного веса стандартной продукции по всей партии изделий с вероятностью 0,954

Задача 2

Имеются следующие данные по предприятию:

Наименование продукции	Количество продукции тыс. шт		Себестоимость изделия, тыс. руб
	Базисный период	Отчетный период	Базисный период	Отчетный период
А	400	450	82,0	80,0
Б	1000	1500	97,0	90,0
В	130	160	46,0	45,0
Итого:

Определите:

1) индивидуальные индексы себестоимости и физического объема продукции;

2) общий индекс себестоимости единицы продукции;

3) индекс затрат на производство продукции;

4) выполните факторный анализ.

На основании исчисленных индексов (2,3), используя взаимосвязи индексов, определите индекс физического объема продукции.

1) =

где - себестоимость продукции отчетного периода

- себестоимость продукции базисного периода

= (А)

= (Б)

= (В)

=

где - объем выпуска продукции в базисном периоде

- объем выпуска продукции в отчетном периоде

= (А)

= (Б)

= (В)

2) =

=

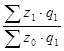
3) = =

Индекс физического объема равен

= ==1,379

4)

Задача 3

Динамика себестоимости и объема продукции «А» на двух заводах характеризуется следующими данными:

Заводы	Себестоимость единицы продукции, тыс. руб.		Выработано продукции, тыс. единиц
	Базисный период	Отчетный период	Базисный период	Отчетный период
1	120	100	2,0	2,0
2	200	180	4,0	6,0

Вычислите:

1) Индекс себестоимости переменного состава.

2) Индекс себестоимости постоянного состава.

3) Индекс структурных сдвигов.

4) Изменение средней себестоимости (в абсолютных величинах) в целом и за счет дейсвий отдельных факторов.

Покажите взаимосвязь исчисленных индексов.

1) =

где - себестоимость продукции отчетного периода

- себестоимость продукции базисного периода

Индекс переменного состава:

2) Индекс постоянного состава:

3) Себестоимость продукции 1го завода в отчетном периоде уменьшилась на 20 тыс. руб, второго завода также уменьшилась на 20 тыс. руб

Взаимосвязь: индекс переменного состава превышает индекс постоянного состава на 0,067

Задача 4

Стоимость основных фондов на начало года, млн р. 18500

Поступило основных фондов, млн р.:

1 марта 120

1 сентября 510

Выбыло основных фондов, млн р.:

1 июля 20

1 ноября 150

Объем выпущенной продукции за год, млн р. 20600

Определить: 1.Среднегодовую стоимость основных фондов;

2. Показатели использования основных фондов;

3. Коэффициент обновления и выбытия.

1) =

где W- стоимость основных фондов на начало года

W- стоимость основных фондов на конец года

W=18500+120+510-20-150=18852

=

2) ФО= (фондоотдача)

Где ТП – объем товарной продукции

- среднегодовая стоимость основных фондов

ФО=

ФЕ= (фондоемкость)

ФЕ=

3) К= К=

К= К=

Задача 5

В 1994 году материалоемкость продукции составила 0,67 р. на 1 р. товарной продукции. В 1995 году объем товарной продукции предприятия увеличился на 9,5 % по сравнению с 1994 г. и составил 25200 тыс.руб., при этом общая сумма материальных затрат возросла на 7,2 %.

Определить в какой степени абсолютное и относительное изменение объема материальных затрат обусловлено:

а) снижением материалоемкости продукции;

б) увеличением объема производства.

МЗ=М где М- материалоемкость

ТП – объем товарной продукции

М(1994)=0,67 р.

ТП(1994)=25200-25200тыс.руб.

ТП(1995)=25200 тыс.руб.

МЗ(1994)=0,67 тыс.руб.

МЗ(1995)=15280 тыс.руб.

М(1995)=р.

а) М снизилась на 0,02 р.

б) ТП увеличилась на 2394 тыс.руб.

Задача 6

Производство цемента характеризуется следующими показателями:

Годы	Цемент, млн.т.
1	72,4
2	80,0
3	84,8
4	87,5
5	89,7
6	95,2

Для анализа ряда динамики исчислите:

1) показатели, характеризующие рост производства цемента: абсолютные приросты, темпы роста и прироста (по годам и к базисному году). Результаты изложите в табличной форме;

2) средний уровень и среднегодовой темп ряда динамики;

3) покажите взаимосвязь между цепными и базисными показателями;

4) для определения основной тенденции ряда произведите выравнивание ряда динамики с помощью уравнения прямой.

Изобразите фактический и выровненные ряды на графике.

1) Т= Т=

По годам

1	2	3	4	5	6
	80-72,4=7,6	84,8-80=4,8	87,5-84,8=2,7	89,7-87,5=2,2	95,2-89,7=5,5
Т

К базисному году

	80-72,4=7,6	84,8-72,4=12,4	87,5-72,4=15,1	89,7-72,4=17,3	95,2-72,4=22,8
Т
Т

2) = =

=

===1,056

3) Исходя из полученных данных мы видим что базисные показатели превышают цепные.

4)

Исходя из фактического и выровненного ряда мы видим, что в период с 1го по 4й годы целесообразно было бы уменьшить объемы производства цемента, а с 4го по 6й годы наоборот увеличить объемы производства цемента.

Задача 7

Работа 24 предприятий отрасли в отчетном периоде характеризуется следующими данными:

ЗАВОДЫ, П/П	Продукция в сопоставимых ценах, млрд.руб.,фактически	Стоимость основных производственных фондов, млрд.руб.
1	2,5	3,5
2	2,8	4,0
3	1,6	1,0
4	12,9	7,0
5	5,6	4,5
6	4,4	4,9
7	2,8	2,8
8	9,4	5,5
9	11,9	6,6
10	2,5	2,0
11	3,5	4,7
12	2,3	2,7
13	3,2	3,0
14	9,6	6,1
15	1,5	2,0
16	4,2	3,9
17	6,4	3,3
18	4,3	3,3
19	1,4	3,0
20	3,0	3,1
21	2,5	3,1
22	7,9	4,5
23	3,6	3,1
24	8,9	5,6
ИТОГО:

С целью изучения зависимости между стоимостью основных производственных фондов и выпуском продукции произведите группировку заводов по размеру основных фондов, образовав 4 группы заводов с равными интервалами. Результаты представьте в виде итоговой таблицы. Проанализируйте полученные данные.

Итоговая таблица

№ группы	Группы заводов по размеру ОПФ(интервалы) млн.руб.	Число заводов	Стоимость ОПФ		Стоимость валовой продукции млн. руб		Фондоотдача
			Всего	в среднем на один завод	Всего	в среднем на один завод
1	1,4 – 4,3	15	45,2	3,01	678	45,2	0,923
2	4,3 – 7,2	3	12,7	4,23	38,1	12,7	1,291
3	7,2 – 10,1	4	21,7	5,43	86,8	21,7	1,649
4	10,1 – 13	2	13,6	6,8	27,2	13,6	1,824
ИТОГО:		24	93,2	19,47	830,1	93,2	5,687

Величина интервала

h=

Стоимость ОПФ:

1. группа 3,5+4,0+1,0+2,8+2,0+4,7+2,7+3,0+2,0+3,9+3,3+3,0+3,1+3,1+3,1=45,2

В среднем

2 группа 4,5+4,9+3,3=12,7

В среднем

3 группа 5,5+6,1+4,5+5,6=21,7

В среднем

4 группа 7,0+6,6=13,6

В среднем

Стоимость ВП = стоимость ОПФ

1 группа 45,2 В среднем 3,01

2 группа 12,7 В среднем 4,23

3 группа 21,7 В среднем 5,43

4 группа 13,6 В среднем 6,8

ФО= (фондоотдача)

1. группа ТП=2,5+2,8+1,6+2,8+2,5+3,5+2,3+3,2+1,5+4,2+4,3+1,4+3,0+2,5+3,6=41,7

ФО=

2 группа ТП=5,6+4,4+6,4=16,4

ФО=

3 группа ТП=9,4+9,6+7,9+8,9=35,8

ФО=

4 группа ТП=12,9+11,9=24,8

ФО=

Итак, больше всего заводов входят в первую группу с интервалом от 1,4 до 4,3. Меньше всего заводов входит в 4 группу с интервалом от 10,1 до 13. Больше всего фондоотдача в 4й группе заводов, а наименьшая в 1й группе, это видно по итоговой таблице.