Название: Гидростатическое давление и его свойства

Вид работы: реферат

Рубрика: Геология

Размер файла: 70.24 Kb

Скачать файл: referat.me-62576.docx

Краткое описание работы: ГИДРОСТАТИКА Гидростатическое давление и его свойства Уравнения гидростатики Некоторые понятия в гидростатике Давление жидкости на плоские и криволинейные поверхности

Гидростатическое давление и его свойства

ГИДРОСТАТИКА

• Гидростатическое давление и его свойства
• Уравнения гидростатики
• Некоторые понятия в гидростатике
• Давление жидкости на плоские и криволинейные поверхности
• Плавание тел

ГИДРОСТАТИКА

Гидростатическое давление и его свойства

Гидростатика — раздел гидравлики, в котором изучаются законы жидкости в состоянии равновесия и распределение давления покоящейся жидкости на различные поверхности.

Рассмотрим основное понятие гидростатики — гидростатическое давление. На рис. 2.1 представлен некоторый произвольный объем покоящейся жидкости. Разделим этот объем плоскостью ВС на две части — I и II. В плоскости ВС выделим площадь ω с центром в точке А. Давление со стороны части I объема будет передаваться на поверхность ВС с силой Р .

Гидростатическим давлением Р называется сила давления жидкости на единицу площади ω, и его можно представить формулой

(2.1)

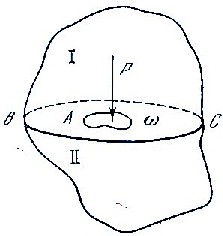
рис. 2.1

Гидростатическое давление имеет размерность в системе СИ Паскаль (Па). Оно обладает тремя свойствами.

Первое свойство. Гидростатическое давление направлено по внутренней нормали к поверхности, на которую оно действует.

Второе свойство. Гидростатическое давление в точке действует одинаково по всем направлениям и может быть выражено соотношением

Px =Py =Pz =Pn

(2.2)

Третье свойство. Гидростатическое давление в точке зависит от ее координат в пространстве и может быть записано следующим образом:

P=f (x, y, z)

(2.3)

Уравнения гидростатики

При изучении законов покоящейся жидкости рассмотрим три уравнения: а) основные дифференциальные уравнения равновесия; б) уравнения гидростатического давления; в) уравнение гидростатического давления жидкости, находящейся под воздействием сил тяжести.

а. Основные дифференциальные уравнения равновесия Л. Эйлера выведены в Российской Академии наук в 1755 г. Уравнения выражают связь между массовыми (объемными) силами, давлением и координатами любой точки жидкости в состоянии равновесия.

Не приводя вывода уравнений, поясним ход рассуждений.

В покоящейся жидкости выделяется какой-либо объем. В данном примере на рис. 2.2 рассматривается параллелепипед с гранями ab с d и a ' b ' c ' d '. На выделенный объем действуют силы поверхностного суммарного гидростатического давления и массовые (объемные) силы. Жидкость находится в равновесии, следовательно поверхностные и массовые силы должны уравновешиваться, т. е. сумма этих сил должна быть равна нулю.

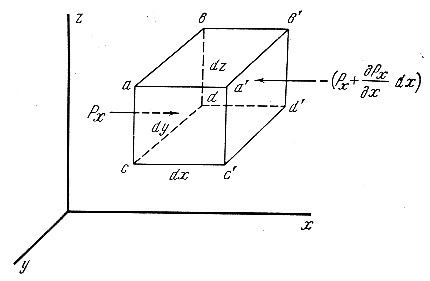
рис. 2.2

ПОВЕРХНОСТНЫЕ СИЛЫ. Силы суммарного гидростатического давления по оси х с учетом приращения дР_х будут равны

(2.4)

Напомним, что силы, направленные по оси, положительны, а про­тив оси — отрицательны. Аналогично можно получить величины по оси у и z .

МАССОВЫЕ (ОБЪЕМНЫЕ) СИЛЫ. Объемной силой назы­вается сила, приложенная к массе жидкости в объеме параллелепи­педа. Такой силой может быть сила тяжести p = mg . При постоянной плотности масса жидкости выделенного объема равна m = r dxdydz . В гидравлике проекции ускорения объемных сил, отнесенных к единице массы, обозначаются X , Y , Z . Таким образом, по оси x можно записать

dPx = Xrdxdydz

(2.5)

Сумма поверхностных и массовых сил по оси x будет равна

Px dydz – Px dydz - dxdydz + Xrdxdydz = 0

Производя сокращения и отнеся все члены уравнения к единице массы, т. е. разделив на величину массы rdxdydz , и учитывая второе свойство гидростатического давления, получим уравнения Л. Эйлера по всем осям

	(2.6)

	(2.7)

Физический смысл полученных уравнений заключается в следующем: изменение гидростатического давления в направлении какой-либо оси, отнесенное к плотности, равняется проекции объемной силы, отнесенной к единице массы, на ту же ось.

б. Уравнение гидростатического давления можно получить из уравнений Л. Эйлера. Если умножить каждый его член на r dx , r dy и rdz и сложить их, то получим

(2.8)

Правая часть полученного уравнения представляет собой полный дифференциал давления

dP = r ( Xdx + Ydy + Zdz )

(2.9)

Из последнего уравнения гидростатического давления видно, что давление зависит от плотности жидкости и бывает больше для плотных жидкостей.

В случае, если имеется поверхность равного давления, Р =const и dP =0, поскольку r не равно 0, то уравнение в случае равного давления имеет вид

Xdx + Ydy + Zdz =0

(2.10)

в. Уравнение гидростатического давления жидкости, находящейся под действием силы тяжести. Основное уравнение гидростатического давления в дифференциальной форме следующее:

dP = r ( Xdx + Ydy + Zdz )

Интегрируя данное уравнение, можно его использовать для различных случаев покоя жидкости. Рассмотрим частный случай, когда жидкость находится в покое под действием силы тяжести. На рис. 2.3 на поверхности жидкости наметим точку в , в которой давление Р₀ . Начало координат совместим с точкой в , а ось z направим вниз. Выделим точку а , в которой жидкость находится под действием силы тяжести, равной весу р= mg . Примем массу m =1, тогда p = g , т. е. единичная массовая сила будет равна ускорению. Проекции этой силы на ось x и y будут равны 0: X =0; Y =0. Проекция силы тяжести на ось z = g , т. к. направление оси совпадает с направлением силы тяжести вниз, к центру Земли.

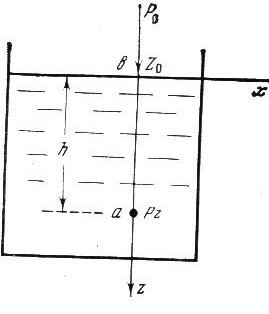
рис. 2.3

Согласно уравнению гидростатического давления dP будет равно

dP=rgdz

(2.11)

Интегрируем это уравнение в пределах от Р₀ до Р и от z₀ до z

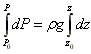получим

P – P0 =rg(z-z0 )

(2.12)

Из рис. 2.3 видно, что глубина погружения точки а относительно свободной поверхности h = z – z ₀ . Поэтому можем записать

P – P 0 =r gh

(2.13)

P = P 0 - rgh

(2.14)

Последняя формула является уравнением гидростатического давления жидкости, находящейся под действием силы тяжести.

Если свободная поверхность жидкости соприкасается с атмосферой, то Р₀ =Р_а и полное гидростатическое давление будет иметь вид

Р=Ра +r gh

(2.15)

Из уравнения гидростатического давления следует закон Паскаля: давление, воспринимаемое жидкостью, передается во все точки жидкости с одинаковой силой.

Избыточным, или манометрическим, давлением называется превышение давления над атмосферным

Ризб = rgh

(2.16)

Некоторые понятия в гидростатике

а. Пьезометрическая высота давления. На рис. 2.4 в состоянии равновесия представлен закрытый сосуд, наполненный жидкостью, на поверхности которой давление Р>Р_а . К стекам сосуда подведены две открытые трубки, называемые пьезометрами («пьезо» - греческое слово – давление, «метр» - измерение). Трубки А и В расположены на разных уровнях z _А и z _В от плоскости сравнения 0-0 . Жидкость в точках А и В , которая находится под давлением Р , поднимется по пьезометрам и, испытывая атмосферное давление Р_а , остановится на одной плоскости 0’-0’ , называемой напорной плоскостью.