Название: Сварные конструкции

Вид работы: курсовая работа

Рубрика: Промышленность и производство

Размер файла: 625.88 Kb

Скачать файл: referat.me-299490.docx

Краткое описание работы: МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ имени Н. Э. БАУМАНА КАФЕДРА МТ7 РАСЧЕТНО-ПОЯСНИТЕЛЬНАЯ ЗАПИСКА К КУРСОВОМУ ПРОЕКТУ «СВАРНЫЕ КОНСТРУКЦИИ»

Сварные конструкции

МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

имени Н. Э. БАУМАНА

КАФЕДРА МТ7

РАСЧЕТНО-ПОЯСНИТЕЛЬНАЯ ЗАПИСКА К КУРСОВОМУ ПРОЕКТУ

«СВАРНЫЕ КОНСТРУКЦИИ»

Москва 2009г.

Аннотация.

Основной задачей курсового проекта является проектирование главной фермы мостового крана в двух вариантах, условно называемых «технологичным» и «экономичным» и их сравнительный анализ. По первому варианту предполагается проектирование с минимальным применением механической обработки: стержни ферм изготавливаются из прокатных элементов, соединяемых внахлестку угловыми швами. По второму варианту необходимо спроектировать ферму минимальной массы, используя элементы, соединяемые встык.

Проект выполнен на 4-х листах формата А1, содержащих: общий вид мостового крана для обоих вариантов, конструкции основных узлов ферм «технологичного» и «экономичного» вариантов, а так же эскизный проект стенда для сборки и сварки концевой балки. Пояснительная записка содержит 49 листов формата А4, на которых представлены расчеты, таблицы и иллюстрации.

В ходе выполнения проекта были рассчитаны усилия в отдельных стержнях фермы, определены необходимые размеры поперечных сечений стержней, удовлетворяющие условиям выносливости, устойчивости и статической прочности, детально разработаны основные пространственные сварные узлы конструкции. Так же были определены основные размеры концевой балки мостового крана и разработана технология ее сборки и сварки.

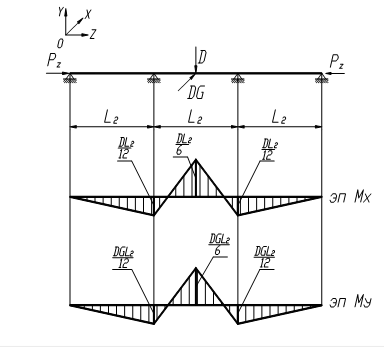
Построение линий влияния

Определение опорных реакций:

Составим уравнение моментов относительно точки В (см. Рис. 2.1.):

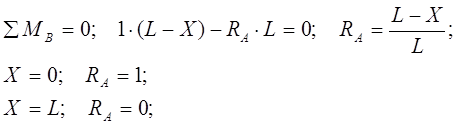
Составим уравнение моментов относительно точки А (см. Рис. 2.1.):

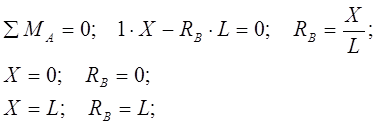
где 1 – единичная сила (далее Е. С.);

Х – координата положения Е. С.;

R_A – реакция в точке А;

R_B – реакция в точке В.

L – пролет фермы.

Линия влияния стержня В11 (см. рис. 2.1):

Е. С. правее точки 11^/ :

Составим уравнение моментов относительно точки 6:

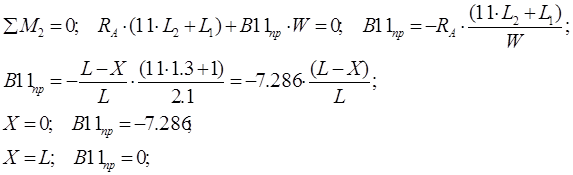
Е. С. левее точки 11 ^/ :

Составим уравнение моментов относительно точки 5:

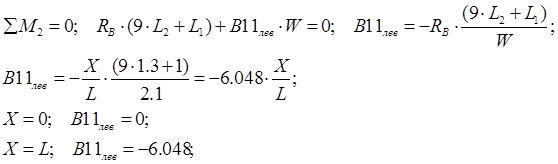
Линия влияния стержня Н6 (см. рис. 2.1):

Е. С. правее точки 11^/ :

Составим уравнение моментов относительно точки 11^/ :

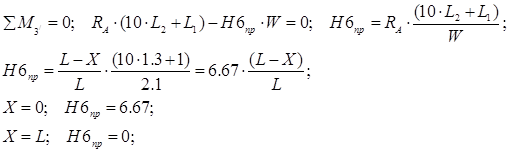
L₁ =1 м – длина крайних стержней верхнего пояса;

L₂ =1,3 м – длина остальных стержней нижнего пояса;

W=2.1 м – высота стоек вертикальной фермы.

Е. С. левее точки 11^/ :

Составим уравнение моментов относительно точки 11^/ :

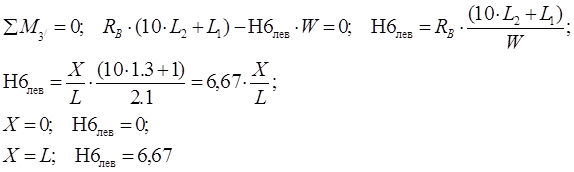
где Н2_лев – усилие в стержне Н2 направленное из точки 2 в точку 1.

Линия влияния стержня Р11 (см. рис. 2.1):

Е. С. правее точки 11^/ :

Составим уравнение проекций сил на вертикальную ось:

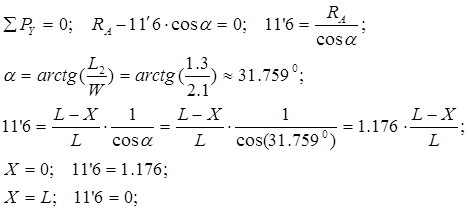
где 3^/ 2 – усилие в стержне Р4 направленное из точки 3^/ в точку 2.

Е. С. левее точки 3^/ :

Составим уравнение проекций сил на вертикальную ось:

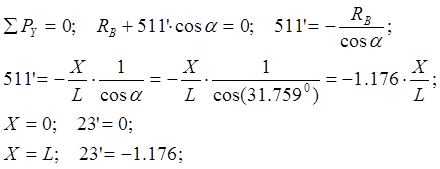
Линия влияния стержня С1 (см. рис. 2.1):

Составим уравнение проекций сил на вертикальную ось в точке 0^/ :

где 0^/ 0 – усилие в стержне С1 направленное из точки 0^/ в точку 0.

Линия влияния стержня С2 (см. рис. 2.1):

Составим уравнение проекций сил на вертикальную ось в точке 2:

где 2^/ 1 – усилие в стержне С2 направленное из точки 2^/ в точку 1.

Определение усилий в стержнях от распределенной и сосредоточенной нагрузки.

Стержень В11:

Усилие от распределенной нагрузки:

где Q=0.24 кН – распределенная нагрузка;

W - площадь, ограниченная линией влияния (заштрихованная область).

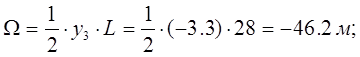
Усилие от сосредоточенной нагрузки:

а) Максимальное усилие:

где D=168,7 кН – вертикальная сила давления от колес тележки;

б) Минимальное усилие:

Стержень Н6:

Усилие от распределенной нагрузки:

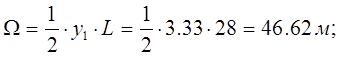
Усилие от сосредоточенной нагрузки:

а) Максимальное усилие:

б) Минимальное усилие:

Стержень Р11:

Усилие от распределенной нагрузки:

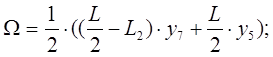
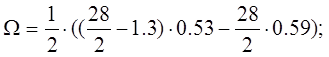
Усилие от сосредоточенной нагрузки:

а) Максимальное усилие:

б) Минимальное усилие:

Стержень С1:

Усилие от распределенной нагрузки:

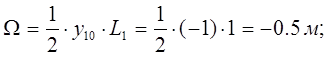
Усилие от сосредоточенной нагрузки:

а) Максимальное усилие:

б) Минимальное усилие:

Стержень С2:

Усилие от распределенной нагрузки:

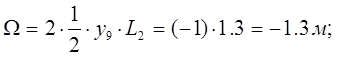
Усилие от сосредоточенной нагрузки:

а) Максимальное усилие:

б) Минимальное усилие:

Усилие в остальных стержнях:

Усилие для остальных стержней от нагрузок, действующих на главную и горизонтальную фермы, найдены с помощью расчетной программы и представлены в приложении.

Вариант N22 Смирнов М Сдан 18/ 2/2009

L= 28.00 P= 450.00 D= 168.70

L1= 1.00 W= 2.10 DG= 20.20

L2= 1.30 W1= .90 Q= .67

LT= 2.50 WG= 1.40 QV= .20

N= 22 WK= 3.30 QG= .10

УСИЛИЯ В СТЕРЖНЯХ :

Г Л А В Н А Я Ф Е Р М А ВСПОМОГАТЕЛЬНАЯ ГОРИЗОНТАЛЬНАЯ

--------------------------- ------------ --------------------

СТЕР- N(Q) N(D)MAX N(D)MIN СТЕР- N(QV) СТЕР- N(QG) N(DG)

ЖЕНЬ KH KH KH ЖЕНЬ KH ЖЕНЬ KH KH

--------------------------- ------------ --------------------

ВЕРХНИЙ ПОЯС ВЕРХН. ПОЯС ПОЯС ГЛАВНОЙ ФЕРМЫ

B 1 .0 .0 .0 B 1 .0 B 1 .0 .0

B 2 -9.4 -322.7 .0 B 2 -2.8 B 2 -2.1 -58.0

B 3 -9.4 -322.7 .0 B 3 -2.8 B 3 -2.1 -58.0

B 4 -18.1 -614.3 .0 B 4 -5.4 B 4 -4.0 -110.3

B 5 -18.1 -614.3 .0 B 5 -5.4 B 5 -4.0 -110.3

B 6 -24.5 -828.4 .0 B 6 -7.3 B 6 -5.5 -148.8

B 7 -24.5 -828.4 .0 B 7 -7.3 B 7 -5.5 -148.8

B 8 -28.8 -964.9 .0 B 8 -8.6 B 8 -6.5 -173.3

B 9 -28.8 -964.9 .0 B 9 -8.6 B 9 -6.5 -173.3

B10 -31.0 -1023.9 .0 B10 -9.3 B10 -6.9 -183.9

B11 -31.0 -1023.9 .0 B11 -9.3 B11 -6.9 -183.9

НИЖНИЙ ПОЯС НИЖНИЙ ПОЯС ПОЯС ВСПОМ. ФЕРМЫ

H 1 7.2 246.2 .0 H 1 2.1 H 1 1.0 26.5

H 2 14.0 478.2 .0 H 2 4.2 H 2 3.1 85.9

H 3 21.6 731.1 .0 H 3 6.4 H 3 4.8 131.3

H 4 27.0 906.4 .0 H 4 8.0 H 4 6.0 162.8

H 5 30.2 1004.1 .0 H 5 9.0 H 5 6.8 180.3

H 6 31.3 1024.3 .0 H 6 9.3 H 6 7.0 184.0

РАСКОСЫ РАСКОСЫ РАСКОСЫ

P 1 -8.6 -293.6 .0 P 1 -2.6 P 1 -1.7 -45.7

P 2 5.8 219.3 .0 P 2 1.7 P 2 1.8 48.1

P 3 -8.7 -328.1 14.9 P 3 -2.6 P 3 -1.5 -45.6

P 4 7.7 309.7 -33.3 P 4 2.3 P 4 1.3 43.0

P 5 -6.7 -291.2 51.7 P 5 -2.0 P 5 -1.2 -40.5

P 6 5.6 272.8 -70.2 P 6 1.7 P 6 1.0 37.9

P 7 -4.6 -254.4 88.6 P 7 -1.4 P 7 -.8 -35.3

P 8 3.6 236.0 -107.0 P 8 1.1 P 8 .6 32.8

P 9 -2.6 -217.5 125.4 P 9 -.8 P 9 -.4 -30.2

P10 1.5 199.1 -143.8 P10 .5 P10 .3 27.7

P11 -.5 -180.7 162.3 P11 -.2 P11 -.1 -25.1

СТОЙКИ СТОЙКИ СТОЙКИ

C 1 -.3 -168.7 .0 C 1 -.1 C 1 -.1 -20.2

C 2 -.9 -168.7 .0 C 2 -.3 C 2 -.1 -20.2

C 3 -.9 -168.7 .0 C 3 -.3 C 3 -.

Определение расчетных усилий в стержнях.

При нахождении усилий в стержнях верхнего пояса главной фермы учитываются усилия в поясах горизонтальной фермы от горизонтальной нагрузки, т.к. эти стержни принадлежат сразу двум фермам.

В формуле для определения отсутствует усилие от сосредоточенной горизонтальной нагрузки N(DG), т.к. при нахождении тележки в положении соответствующем N(DG) вместо усилия появится , и найденное таким образом усилие не будет минимальным.

Главная ферма:

Верхний пояс:

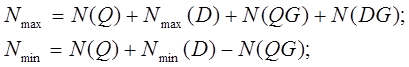
где N_max – максимальное усилие в стержне;

N_min – минимальное усилие в стержне;

N(Q) – усилие в стержне от распределенной нагрузки;

N(QG) – усилие в стержне от распределенной горизонтальной нагрузки;

N(DG) – усилие в стержне от горизонтальной инерционной нагрузки;

N_min (D) – минимальное усилие от силы давления колес тележки в стержне;

N_max (D) – максимальное усилие от силы давления колес тележки в стержне.

Нижний пояс:

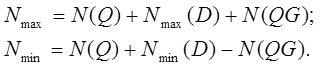
Раскосы:

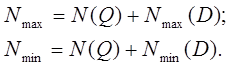
Стойки:

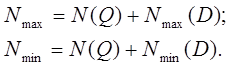
Горизонтальная ферма:

Раскосы:

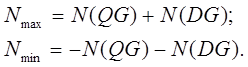
Стойки:

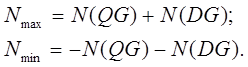
Коэффициент асимметрии цикла:

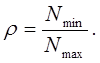
Результаты расчетов:

Результаты расчетов по приведенным выше формулам сведены в таблицу 4.1.

Таблица 4.1. Максимальные и минимальные усилие в стержнях главной и горизонтальной фермы.

Стержень	Главная ферма			Горизонтальная ферма
	Nmax , kH	Nmin , kH	r	Nmax , kH	Nmin , kH	r
В1	0	0	0
В2	-392,2	-7,3	0,0186
В3	-392,2	-7,3	0,0186
В4	-746,7	-14,1	0,0189
B5	-746,7	-14,1	0,0189
B6	-1007	-19	0,0189
B7	-1007	-19	0,0189
B8	-1173	-22,3	0,019
B9	-1173	-22,3	0,019
B10	-1246	-24,1	0,193
B11	-1246	-24,1	0,193
Н1	254,4	6,2	0,0244
Н2	495,3	10,9	0,0220
H3	757,5	16,8	0,0222
H4	939,4	21	0,0224
H5	1041	23,4	0,0225
H6	1063	24,3	0,0229
Р1	-302,2	-8,6	0,0285	-47,4	47,4	-1
Р2	225,1	5,8	0,0258	49,9	-49,9	-1
Р3	-336,8	6,2	-0,0180	-47,1	47,1	-1
Р4	317,4	-25,6	-0,0807	44,3	-44,3	-1
P5	-297,9	45	-0,1511	-41,7	41,7	-1
P6	278,4	-64,6	-0,2320	38,9	-38,9	-1
P7	-259,0	84	-0,3243	-36,1	36,1	-1
P8	239,6	-103,4	-0,4316	33,4	-33,4	-1
P9	-220,1	122,8	-0,5579	-30,6	30,6	-1
P10	200,6	-142,3	-0,7094	28	-28	-1
P11	-181,2	161,8	-0,8929	-25,2	25,2	-1
С1	-169,0	-0,3	0,0017	-20,3	20,3	-1
С2	-169,6	-0,9	0,0053	-20,3	20,3	-1
С3	-169,6	-0,9	0,0053	-20,3	20,3	-1

Расчет главной фермы первого варианта.

Верхний пояс:

Схема нагружения и исходные данные:

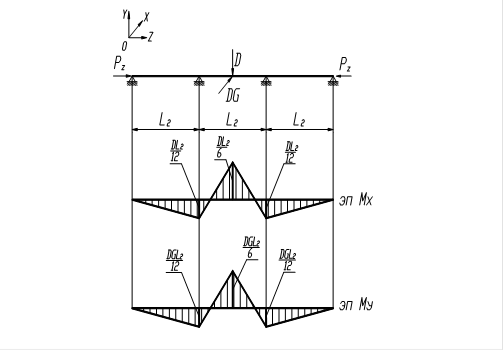
P_z =1246 кН;

L₂ =1300 мм;

D=168,7 кН;

DG=20,2 кН;

ρ=0.0193;

Материал: ВСт3сп;

Расчетная группа по СНиП 4-я

Рис. 5.1. Схема нагружения верхнего пояса главной фермы.

Расчетная схема:

Х, Y - центральные оси сечения;

s – толщина стенки двутавра;

Н – высота двутавра;

b – ширина полки двутавра.

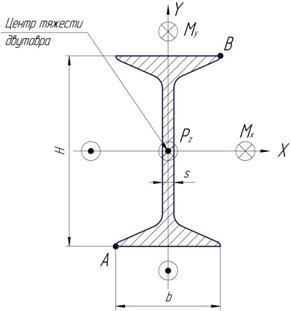
Рис. 5.2 . Расчетная схема поперечного сечения верхнего пояса.

Допускаемые напряжения при статическом нагружении:

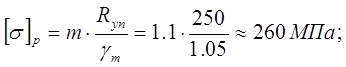
где [σ]_р – допускаемое напряжение при растяжении;

m=1.1 – коэффициент неполноты расчета (учитывает влияние горизонтальной фермы);

R_yn =250 МПа – нормативное сопротивление при растяжении;

γ_m =1.05 – коэффициент надежности по материалу.

Допускаемое напряжение при работе на выносливость:

где α – коэффициент учитывающий число циклов нагружения (n=10⁶ );

γ_v – коэффициент учитывающий асимметрию цикла нагружения;

R_v =75 МПа – расчетное сопротивление (для 4-ой группы);

ρ=0,019 – коэффициент асимметрии цикла (для стержня В11 – наиболее нагруженного);

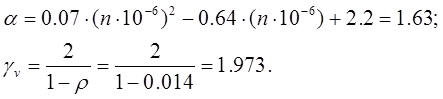
Расчетные изгибающие моменты:

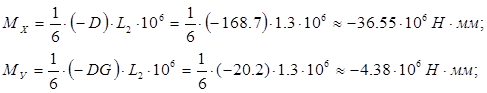
где М_х – изгибающий момент относительно оси X;

М_у – изгибающий момент относительно оси Y;

Определение необходимой площади:

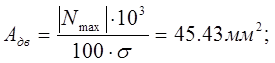
Подбор типоразмера двутавра:

Подбор типоразмера двутавр производился методом перебора, то есть берется произвольный двутавра и производятся расчет:

1. На статическую прочность;

2. На устойчивость;

3. На сопротивление усталости.

Если требования хотя бы одного из расчета не выполнялись, то берется следующий типоразмер двутавра и расчеты производятся заново, до тех пор, пока не выполнится условие всех расчетов.

Принимаем двутавр №40 ГОСТ 8239-89:

А_дв =72,6 см² – площадь двутавра;

h=400 мм – высота двутавра;

b=155 мм – ширина полки двутавра;

s=8,3 мм – толщина стенки двутавра;

J_x =19062 см⁴ – момент инерции Х-Х двутавра;

J_y =667 см⁴ – момент инерции Y-Y двутавра;

W_x =953 см³ – момент сопротивления двутавра;

W_y =86,1 см³ – момент сопротивления двутавра;

i_x =16,2 см – радиус инерции поперечного сечения;

i_y =3,03 см – минимальный радиус инерции поперечного сечения;

Проверочный расчет на статическую прочность:

Прочность данного сечения необходимо проверить в двух точках: А и Б (см. рис. 5.2.).

Напряжение в точке А:

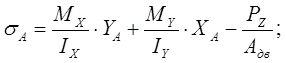
где Y_A =h/2=400/2=200 мм – координата точки А по оси Y;

Х_А =b/2=155/2=77,5 мм – координата точки А по оси Х;

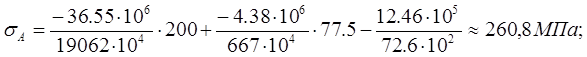
Напряжение в точке Б:

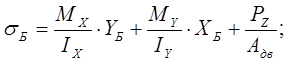
где Y_Б =h/2=200/2=100 мм – координата точки Б по оси Y;

Х_Б =Х_А =50 мм – координата точки Б по оси Х;

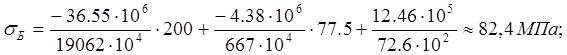
Статическая прочность в точке Б обеспечивается.

Заключение:

Статическая прочность обеспечивается во всех точках сечения.

Проверочный расчет общей устойчивости:

Определим относительный эксцентриситет:

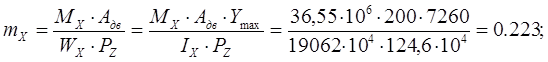
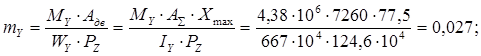
m_y и m_x - относительный эксцентриситет (коэффициент показывающий, как работает стержневой элемент, как балка или стойка);

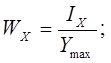-момент сопротивления изгибу поперечного сечения относительно оси OX;

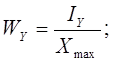-момент сопротивления изгибу поперечного сечения относительно оси OY;

X_max =b/2=150/2=77,5 – максимальная координата поперечного сечения по оси X;

Y_max =h/2=400/2=200 мм – максимальная координата поперечного сечения по оси Y;

Определим гибкость пояса:

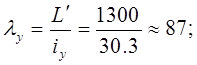
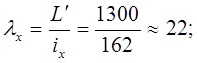
где L’- длина полуволны изогнутой оси стержневого элемента;

μ=1 – коэффициент Элейра (учитывает тип закрепления стержневого элемента);

Условие устойчивости:

В случаи, когда на поперечное сечение действует два изгибающих момента необходимо произвести две проверки устойчивости:

1. В плоскости действия максимального изгибающего момента М_Х ;

2. В случаи совместного действия изгибающих моментов М_Х и М_Y .

В плоскости действия максимального изгибающего момента М_Х :

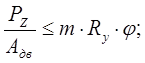- условие устойчивости;

где φ=0.987 – коэффициент понижение допускаемых напряжений (выбирается в зависимости от λ_х и R_у по СНиП табл.72);

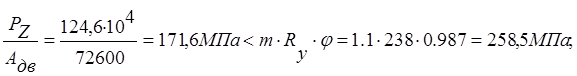
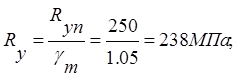
Общая устойчивость в плоскости действия максимального изгибающего момента М_х обеспечивается.

В случаи совместного действия изгибающих моментов М_Х и М_Y :

По пункту 5.34 СНиП устойчивость проверяется по формуле:

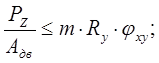- условие устойчивости;

где φ_xу – коэффициент учитывающий влияния двух изгибающих моментов М_Х и М_Y на устойчивость;

φ^/ _у =0.804 – коэффициент понижение допускаемых напряжений (выбирается по табл.74 СНиП);

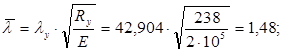
- коэффициент учитывающей влияния изгибающего момента М_Y на устойчивость ;

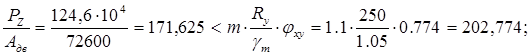
Общая устойчивость в случае совместного действия изгибающих моментов М_х и М_Y обеспечивается.

Заключение:

Общая устойчивость стержневого элемента обеспечивается.

Проверочный расчет на сопротивление усталости:

Условие прочности:

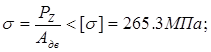
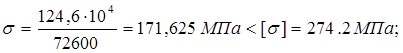
Заключение:

Сопротивление усталости обеспечивается.

Нижний пояс.

Схема нагружения и исходные данные:

P_Z =1063 кН;

ρ=0.0229;

Тип сечения: двутавр;

Рис. 5.3. Схема нагружения нижнего пояса главной фермы. Материал: ВСт3сп;

Расчетная группа по СНиП: 4-я.

Допускаемое напряжение при работе на выносливость:

R_v =75 МПа – для 4-ой группы нагружения;

Так как растяжение:

Определение типоразмера двутавра:

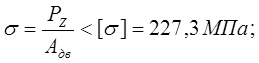- условие прочности;

требуемая площадь двутавра:

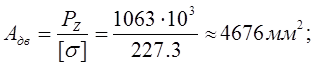
Выбираем двутавр №30AГОСТ 8239-89:

А_дв =49,9 см² – площадь двутавра;

h=300 мм – высота двутавра;

b=145 мм – ширина полки двутавра;

s=6,5 мм – толщина стенки двутавра;

J_x =7780 см⁴ – момент инерции Х-Х двутавра;

J_y =436 см⁴ – момент инерции Y-Y двутавра;

W_x =518 см³ – момент сопротивления двутавра;

W_y =60,1 см³ – момент сопротивления двутавра;

i_x =12,5 см – радиус инерции поперечного сечения;

i_y =2,95 см – минимальный радиус инерции поперечного сечения;

Для растянутых поясов допускаемая гибкость 150.

Радиус инерции относительно оси y :

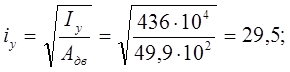
Определим гибкость пояса:

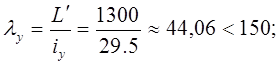
условие выполнено

Расчет на общую устойчивость проводить не требуется, так как стержень всегда растянут.

Раскосы.

Схема нагружения и исходные данные:

Тип сечения: два неравнополочных уголка.

Материал: ВСт3сп;

Расчетная группа по СНиП: 7-я.

Рис. 5.4. Схема нагружения раскосов главной фермы.

Как видно из таблицы 4.1, неизвестно какой раскос имеет самое опасное сочетание нагрузок, поэтому расчет на сопротивление усталости будем производить для всех.

Выбор типоразмера уголка:

- допускаемое напряжение;

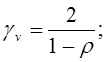- для раскоса Р1;

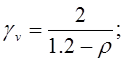- для раскоса Р2;

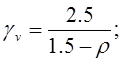- для раскосов Р3- Р11;

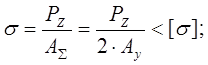- условие прочности;

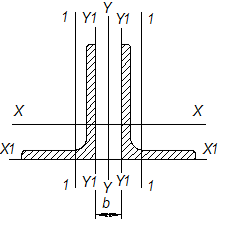
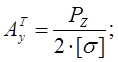- требуемая площадь одного уголка;

Результаты расчета сведены в таблицу 5.3.

Таблица 5.3. Подбор типоразмера уголка.

№ раскоса	PZ , кН	ρ	γv	[σ], МПа	Aт у , мм2
Р1	-302,2	0,0285	2,059	132,883	1137,1
Р2	225,1	0,0258	1,703	109,944	1021,4
Р3	-336,8	-0,0180	1,646	106,276	1584,6
Р4	317,4	-0,0807	1,582	102,088	1554,5
P5	-297,9	-0,1511	1,514	97,735	1524,0
P6	278,4	-0,2320	1,443	93,170	1494,0
P7	-259,0	-0,3243	1,370	88,456	1464,0
P8	239,6	-0,4316	1,294	83,542	1434,0
P9	-220,1	-0,5579	1,215	78,415	1403,4
P10	200,6	-0,7094	1,132	73,038	1373,3
P11	-181,2	-0,8929	1,045	67,437	1343,5

Как видно из таблицы 5.3 требуемая площадь уголка А_у =1584,6 мм² (раскос Р3). Выбираем уголок №12,5 ГОСТ 8510-86, площадь уголка А_у =1598 мм² ;

Проверочный расчет общей устойчивости:

Определяем гибкость стержня:

Момент инерции должен быть достаточным, для обеспечения гибкости менее 120.

Расстояние между уголками принимаем равным b=6 мм.

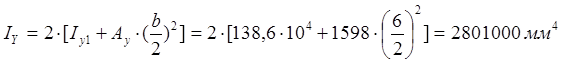- момент инерции относительно оси Y.

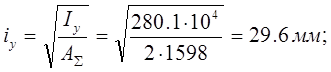- радиус инерции относительно оси Y;

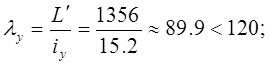
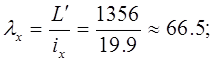
где 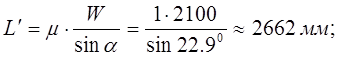- длина полуволны изогнутой оси стержневого элемента;

μ=1 – коэффициент Элейра (учитывает тип закрепления стержневого элемента);

- гибкость стержня относительно оси У;

Соединим стержень одной планкой, посередине. Тогда расстояние между планками будет равно l₁ =L’/2:

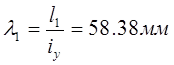- гибкость одной оси;

Условие устойчивости:

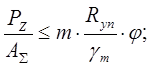
где φ=0.478 – коэффициент понижение допускаемых напряжений (выбирается в зависимости от большей гибкости λ и R_у по табл.72 СНиП);

Общая устойчивость обеспечивается.

Стойки:

Схема нагружения и исходные данные:

Тип сечения: два уголка;

Материал: ВСт3сп;

Расчетная группа по СНиП: 7-я.

Рис. 5.5. Схема нагружения стоек главной фермы. P_z =169.6 кН;

ρ=0.005.

Выбор типоразмера уголка:

- допускаемое напряжение;

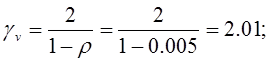
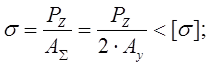- условие прочности;

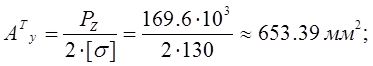- требуемая площадь одного уголка;

Выбираем уголок №9/5,6 ГОСТ 8510-86. Площадь уголка А_у =786 мм² ;

Проверочный расчет общей устойчивости:

Определяем гибкость стержня:

Момент инерции должен быть достаточным, для обеспечения гибкости менее 150.

Расстояние между уголками принимаем равным b=6 мм.

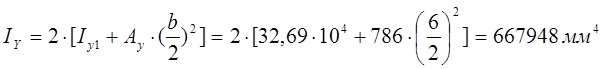- момент инерции относительно оси Y.

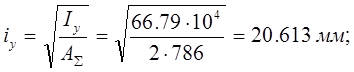- радиус инерции относительно оси Y;

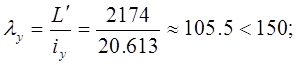
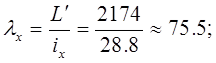
где 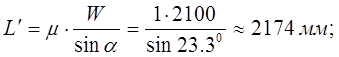- длина полуволны изогнутой оси стержневого элемента;

μ=1 – коэффициент Элейра (учитывает тип закрепления стержневого элемента);

- гибкость стержня относительно оси У;

Соединим стержень одной планкой, посередине. Тогда расстояние между планками будет равно l₁ =L’/2:

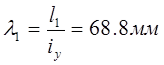- гибкость одной оси;

Условие устойчивости:

;

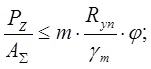где φ=0.419 – коэффициент понижение допускаемых напряжений (выбирается в зависимости от большей λ и R_у по табл.72 СНиП);

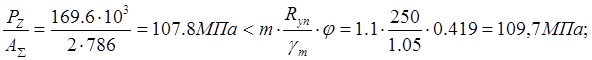
Заключение:

Общая устойчивость обеспечивается.

Расчет главной фермы второго варианта.

По второму варианту, условно называемому «экономичный» предполагается изготовление фермы минимальной массы, используя элементы, соединяемые встык.

Верхний пояс:

Наиболее нагруженный стержень – В11.

Схема нагружения и исходные данные:

P_z =1246 кН;

L₂ =1300 мм;

D=168,7 кН;

DG=20,2 кН;

ρ=0.019;

Материал: ВСт3сп;

Расчетная группа по СНиП4-я

Рис. 5.1. Схема нагружения верхнего пояса главной фермы.

Расчетная схема:

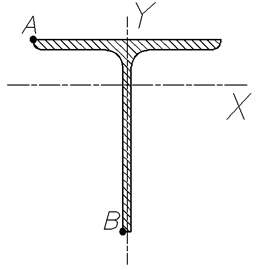
Расчетные изгибающие моменты:

где М_х – изгибающий момент относительно оси X;

М_у – изгибающий момент относительно оси Y;

Допускаемые напряжения при статическом нагружении:

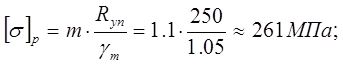
где [σ]_р – допускаемое напряжение при растяжении;

m=1.1 – коэффициент неполноты расчета (учитывает влияние горизонтальной фермы);

R_yn =250 МПа – нормативное сопротивление при растяжении;

γ_m =1.05 – коэффициент надежности по материалу.

Рис. 5.2 . Расчетная схема поперечного сечения верхнего пояса.

Допускаемое напряжение при работе на выносливость:

где α – коэффициент учитывающий число циклов нагружения (n=10⁶ );

γ_v – коэффициент учитывающий асимметрию цикла нагружения;

R_v =75 МПа – расчетное сопротивление (для 4-ой группы);

ρ=0,019 – коэффициент асимметрии цикла (для стержня В11 – наиболее нагруженного);

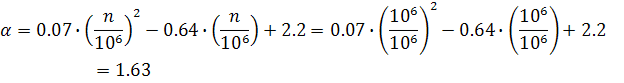
Определение необходимой площади:

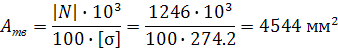
Подбор типоразмера тавра:

Подбор типоразмера тавр производился методом перебора, то есть берется произвольный тавр и производятся расчет:

1. На статическую прочность;

2. На устойчивость;

3. На сопротивление усталости.

Если требования хотя бы одного из расчета не выполнялись, то берется следующий типоразмер тавра и расчеты производятся заново, до тех пор, пока не выполнится условие всех расчетов.

Принимаем тавр №70Б1 ГОСТ 26020-83:

А_тв =79,9 см² – площадь тавра;

h=345,5 мм – высота тавра;

b=260 мм – ширина полки тавра;

s=12 мм – толщина стенки тавра;

J_x =9562 см⁴ – момент инерции Х-Х тавра;

J_y =2271 см⁴ – момент инерции Y-Y тавра;

W_x =379.3 см³ – момент сопротивления тавра;

W_y =174.7 см³ – момент сопротивления тавра;

i_x =10,94 см – радиус инерции поперечного сечения;

i_y =5,33 см – минимальный радиус инерции поперечного сечения;

Проверочный расчет на статическую прочность:

Прочность данного сечения необходимо проверить в двух точках: А и Б (см. рис. 5.2.).

Напряжение в точке А:

где у=у₀ =34,7 мм;

х=b/2=115/2=57,2 мм;

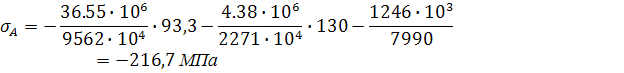
Напряжение в точке В:

где у=s/2=6 мм;

х=c=252,2 мм;

Заключение:

Статическая прочность обеспечивается.

Проверочный расчет общей устойчивости:

Определим относительный эксцентриситет:

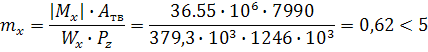
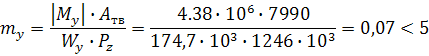
m_y и m_x - относительный эксцентриситет (коэффициент показывающий, как работает стержневой элемент, как балка или стойка);

Определим гибкость пояса:

Верхний пояс рассчитываем как «стойку».

где μ=1 – коэффициент Элейра (учитывает тип закрепления стержневого элемента);

Условие устойчивости:

В случаи, когда на поперечное сечение действует два изгибающих момента необходимо произвести две проверки устойчивости:

1. В плоскости действия максимального изгибающего момента М_Х ;

2. В случаи совместного действия изгибающих моментов М_Х и М_Y .

В плоскости действия максимального изгибающего момента М_Х :

Где φ=0.931 – коэффициент понижение допускаемых напряжений (выбирается в зависимости от λ_х и R_у по СНиП табл.72);

Общая устойчивость в плоскости действия максимального изгибающего момента М_х обеспечивается.

В случаи совместного действия изгибающих моментов М_Х и М_Y :

По пункту 5.34 СНиП устойчивость проверяется по формуле:

- условие устойчивости;

где φ_xу – коэффициент учитывающий влияния двух изгибающих моментов М_Х и М_Y на устойчивость;

φ^/ _у =0.711 – коэффициент понижение допускаемых напряжений (выбирается по табл.74 СНиП);

По таблице 10 СНиПа: ;

- коэффициент учитывающей влияния изгибающего момента М_Y на устойчивость;

Общая устойчивость в случае совместного действия изгибающих моментов М_х и М_Y обеспечивается.

Заключение:

Общая устойчивость стержневого элемента обеспечивается.

Проверочный расчет на сопротивление усталости:

Условие прочности:

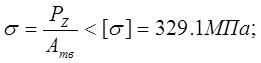
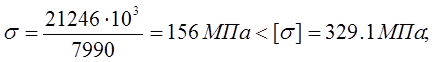
Заключение:

Сопротивление усталости обеспечивается.

Нижний пояс.

Схема нагружения и исходные данные:

P_Z =191,7 кН;

ρ=0.016;

Тип сечения: тавр;

Рис. 5.3. Схема нагружения нижнего пояса главной фермы. Материал: ВСт3сп;

Расчетная группа по СНиП: 4-я.

Расчетная схема:

рис. 5.2 . Расчетная схема поперечного сечения верхнего пояса.

Допускаемые напряжения при статическом нагружении:

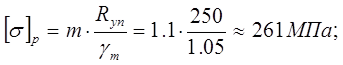
где [σ]_р – допускаемое напряжение при растяжении;

m=1.1 – коэффициент неполноты расчета (учитывает влияние горизонтальной фермы);

R_yn =250 МПа – нормативное сопротивление при растяжении;

γ_m =1.05 – коэффициент надежности по материалу.

Допускаемое напряжение при работе на выносливость:

где α – коэффициент учитывающий число циклов нагружения (n=10⁶ );

γ_v – коэффициент учитывающий асимметрию цикла нагружения;

R_v =75 МПа – расчетное сопротивление (для 4-ой группы);

ρ=0,023 – коэффициент асимметрии цикла (для стержня Н6 – наиболее нагруженного);

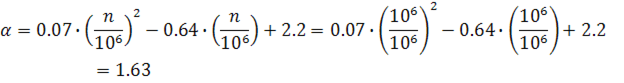
Определение необходимой площади:

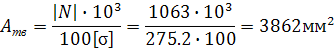
Подбор типоразмера тавра:

Подбор типоразмера тавр производился методом перебора, то есть берется произвольный тавр и производятся расчет на устойчивость.

Если требования хотя бы одного из расчета не выполнялись, то берется следующий типоразмер тавра и расчеты производятся заново, до тех пор, пока не выполнится условие всех расчетов.

Принимаем тавр №40 ГОСТ 8239-89:

А_тв =41,69 см² – площадь тавра;

h=255 мм – высота тавра;

b=160 мм – ширина полки тавра;

s=9 мм – толщина стенки тавра;

Для растянутых поясов допускаемая гибкость 150.

Радиус инерции относительно оси y :

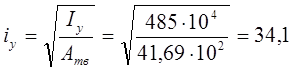
Определим гибкость пояса:

где μ=1 – коэффициент Элейра (учитывает тип закрепления стержневого элемента);

условие выполнено

Расчет на общую устойчивость проводить не требуется, так как стержень всегда растянут.

Раскосы.

Схема нагружения и исходные данные:

Тип сечения: труба;

Материал: ВСт3сп;

Расчетная группа по СНиП: 4-я.

Рис. 5.4. Схема нагружения раскосов главной фермы.

Наиболее нагруженный стержень – Р3: P_Z =336,8 кН и ρ=0.018

Расчет на выносливость

Расчет на выносливость проводится для наиболее растянутого стержня Р4.

Требуемая поперечная площадь стержней из расчета на прочность при растяжении (сжатии):

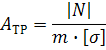
где m =1.1 коэффициент неполноты расчета металлоконструкций.

Допускаемое напряжение определяется как меньшее из двух значений .

:

Стыковой шов со снятым усилением при соединении элементов разной толщины и ширины соответствует 4-0й группе по СНИП.

В этом случае расчетное сопротивление .

Для 3-ей группы и при числе циклов коэффициент

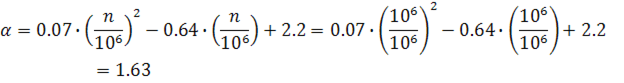
Коэффициент асимметрии цикла

Коэффициент при растяжении чередующимся со сжатием ()

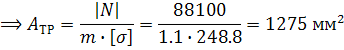
Принимаем толщину стенки трубы

Выбираем трубу 180х2.5 ГОСТ 8734-75 с площадью поперечного сечения

Момент инерции поперечного сечения

Радиус инерции поперечного сечения

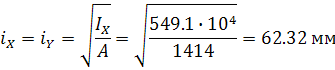
Требуемая гибкость стержня обеспечена.

Расчет на общую устойчивость

Для снижения массы конструкции растянутые (стержни у которых максимальная нагрузка растягивающая) и сжатые (стержни у которых максимальная нагрузки сжимающая) раскосы будут выполнены из труб различного диаметра.

Расчет на устойчивость для наиболее сжатого из растянутых раскосов Р8

По таблице 72 приложения 6 СНиП для :

Общая устойчивость стержня проверяется по формуле

Устойчивость обеспечивается.

Расчет на устойчивость для наиболее сжатого раскоса Р3

Для выбранной трубы 180х2.5 ГОСТ 8734-75 устойчивость не обеспечивается:

Выбираем трубу 180х2.8 ГОСТ 8734-58* с площадью поперечного сечения

Момент инерции поперечного сечения

Радиус инерции поперечного сечения

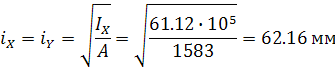
По таблице 72 приложения 6 СНиП для :

Общая устойчивость стержня проверяется по формуле

Сечение подобрано верно, т.к. допустимые напряжения превышают действующие менее чем на 5%.Следовательно, растянутые раскосы главной фермы будут изготавливаться из труб 180х2.5-3-А ГОСТ 8734-75, а сжатые из труб 180х2.8 ГОСТ 8734-75.

Стойки.

Схема нагружения и исходные данные:

Тип сечения: труба;

Материал: ВСт3сп;

Расчетная группа по СНиП: 4-я.

Рис. 5.4. Схема нагружения стоек главной фермы.

Наиболее нагруженный стержень – С3: P_Z =169,6 кН и ρ=0.005.

Допускаемое напряжение при работе на выносливость:

где α – коэффициент учитывающий число циклов нагружения (n=10⁶ );

γ_v – коэффициент учитывающий асимметрию цикла нагружения;

R_v =75 МПа – расчетное сопротивление (для 4-ой группы);

ρ=0,005 – коэффициент асимметрии цикла (для стержня c3 – наиболее нагруженного);

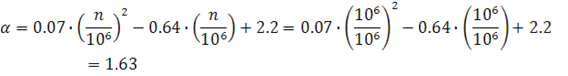
Определение необходимой площади:

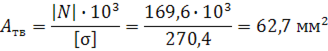
Подбор типоразмера трубы:

Подбор типоразмера трубы производился методом перебора, то есть берется произвольный труба и производятся расчет на устойчивость.

Принимаем трубу 110х2,5 ГОСТ 8734-75:

Проверочный расчет общей устойчивости:

Определим гибкость пояса:

Для растянутых поясов допускаемая

коэффициент Элейра (учитывает тип закрепления стержневого элемента

инерции о

радиус инерции

устойчивост

Где φ=0.805 – коэффициент понижение допускаемых напряжений (выбирается

Общая устойчивость

Расчет горизонтальной фермы.

Изготовление стержней

Для стержней горизонтальной фермы используем равнобокие уголки, которые приварены

Раскосы.

Схема нагружения и исходные данные:

Расчетная группа по СНиП: 7-я.

P_Z =49.9 кН;

Выбираем уголок №8 ГОСТ 8509-93. Площадь уголка А_у =863 мм² ;

Проверочный расчет общей устойчивости:

требуемая площадь одного уголка;

условие прочности;

Определяем гибкость стержня:

Момент инерции должен быть достаточным, для обеспечения гибкости менее 250

гибкость 120.

μ=1 – );

Момент тносительно оси y :

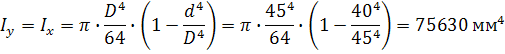
Определим относительно оси y :

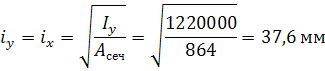
Проверка и:

в зависимости от λ_х и R_у по СНиП табл.72);

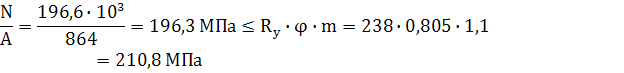
Заключение:

стержневого элемента обеспечивается.

горизонтальной фермы из труб не технологично. внахлест.

Тип сечения: уголок.

Материал: ВСт3сп;

Выбор типоразмера уголка:

- допускаемое напряжение;

- -

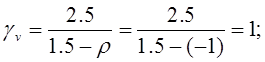
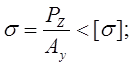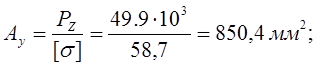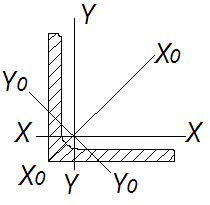
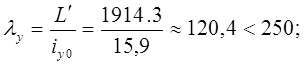
где 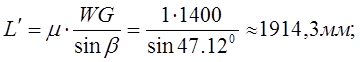- длина полуволны изогнутой оси стержневого элемента;

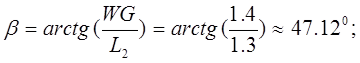- угол наклона раскоса горизонтальной фермы;

μ=1 – коэффициент Элейра (учитывает тип закрепления стержневого элемента);

- радиус инерции относительно оси Y₀ ;

Условие устойчивости:

;

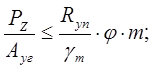где φ=0.419 – коэффициент понижение допускаемых напряжений (выбирается в зависимости от λ и R_у по табл.72 СНиП);

m=1 – коэффициент неполноты расчета металлоконструкции при расчете горизонтальной фермы.

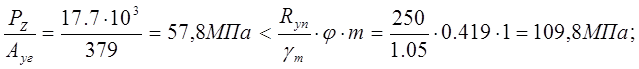
Общая устойчивость обеспечивается.

Стойки:

Схема нагружения и исходные данные:

Тип сечения: Уголок.

Материал: ВСт3сп;

Расчетная группа по СНиП: 7-я.

Рис. 6.2. Схема нагружения стоек горизонтальной фермы. P_Z =20.3 кН;

ρ=-1

Выбор типоразмера уголка:

- допускаемое напряжение;

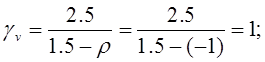
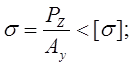- условие прочности;

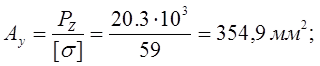- требуемая площадь одного уголка;

Выбираем уголок №5 ГОСТ 8509-93. Площадь уголка А_у =389 мм² ;

Проверочный расчет общей устойчивости:

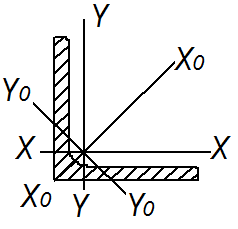
Гибкость стержня:

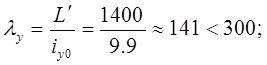
где - длина полуволны изогнутой оси стержневого элемента;

μ=1 – коэффициент Эйлера (учитывает тип закрепления стержневого элемента);

- радиус инерции уголка относительно оси Y₀ ;

Условие устойчивости:

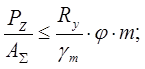
где φ=0.315 – коэффициент понижение допускаемых напряжений (выбирается в зависимости от λ и R_у по табл.72 СНиП);

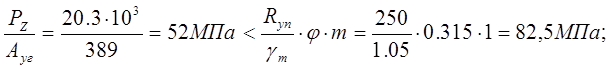
Общая устойчивость обеспечивается.

Расчет пространственных раскосов

Пространственные раскосы, ввиду отсутствия усилий в них, при допущениях принятых в расчете, проверяем только на допускаемую гибкость.

Допускаемая гибкость пространственных раскосов 250

Длина пространственного раскоса:

Выбираем по ГОСТ 8509-72 уголок №5.6, 56х56х4 с площадью поперечного сечения 438 мм²

Радиус инерции относительно оси Y₀ : I_{y 0} =5.41 см⁴

Гибкость стержня:

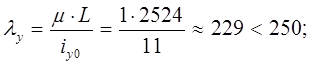
Условие обеспечено.

Для пространственных раскосов принимаем уголок №5.6, 56х56х4 по ГОСТ 8509-93.

Расчет концевой балки

Длина концевой балки

Для обеспечения устойчивости крана(во избежание схода крана с рельс):

, где L = 28000 мм – длина фермы.

Длину концевой балки примем равной

Расчет действующих изгибающих моментов в сечении

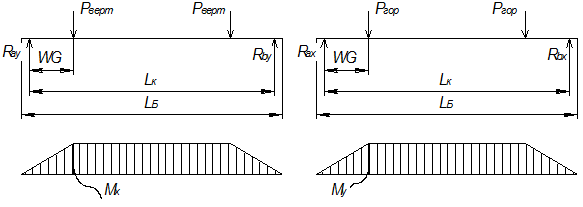
Схема нагружения и эпюры изгибающих моментов в концевой балке

Момент в вертикальной плоскости:

Реакции опор

Момент в горизонтальной плоскости:

Реакции опор

Проверка прочности сечения

Рис. .. Поперечное сечение концевой балки

Концевая балка представляет собой балку коробчатого сечения материал Ст3сп ГОСТ 535-88 (рис. ..):

Высота концевой балки

Ширина концевой балки

Расстояние между стенками балки

Толщину стенок и полок концевой балки примем равной

Момент инерции относительно оси X :

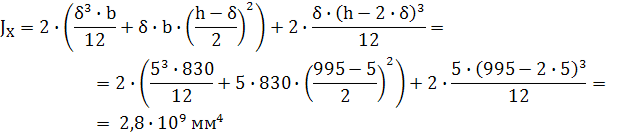
Момент инерции относительно оси Y :

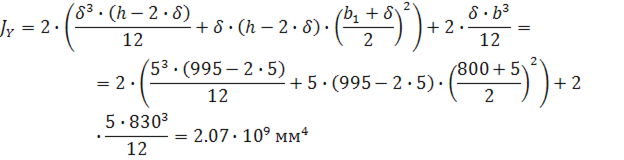
Допускаемое напряжение:

Для стали Ст3сп ГОСТ 535-88 расчетное сопротивление

Коэффициент неполноты расчета для концевой балки , т.к. мы не учитываем закручивание балки.

Расчетное напряжение:

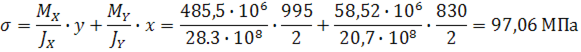
Расчет массы главной фермы

Общая масса главной фермы по первому варианту будет складываться из массы поясов, стоек и раскосов:

,

где

Общая масса стержней каждого типа рассчитывается по формуле:

,

где

Для первого варианта главной фермы:

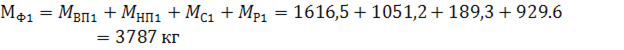
Для второго варианта главной фермы:

Расчет сварных соединений.

Главная ферма ( по первому варианту):

Для угловых швов проверка производится по формуле

, где

равным

отсюда следует, что

– площадь наименьшего сечения швов

– коэффициент, учитывающий форму шва, и равный.

– катет сварного шва

Крепление главной фермы к концевой балке:

Расчетная схема:

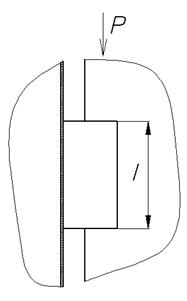
Рис. Расчетная схема для проверки прочности сварного соединения главной фермы с концевой балкой

Расчетная нагрузка:

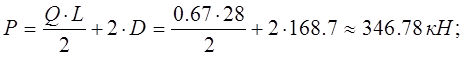
где 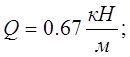- распределенная нагрузка на главную ферму;

- пролет фермы;

- вертикальная сила от давления колес тележки;

Условие прочности сварного соединения:

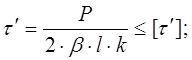
где - коэффициент учитывающей способ сварки;

– длина сварного шва;

- допускаемое напряжение для сварных швов;

- катет сварного шва.

Длина сварного шва:

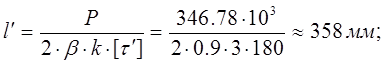
Для обеспечения надежного соединения фланговые швы делаем длиной l_Ф =360 мм каждый и лобовые швы по l_Л =30 мм минимально допустимыми.

Расчет крепления раскосов и стоек к косынкам(первого варианта):

Расчетная схема:

Расчет швов раскоса первого варианта:

k=8 мм

Определим необходимую длину швов

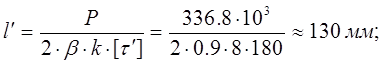
l_л =125 мм

фланговые швы делаем минимально допустимыми l_ф =30 каждый.

Расчет швов стойки первого варианта:

k=3 мм

Определим необходимую длину швов

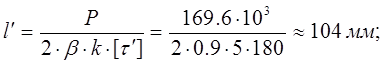
l_л =90 мм

l_ф =30 мм

Расчет сварного шва соединяющего нижний пояс с концевой балкой (первый и второй вариант)

Определим необходимую длину швов

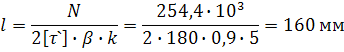
фланговые швы делаем по . c запасом

Горизонтальная ферма:

Как и для главной фермы прочность сварных соединений проверяется по формуле

, где

а площадь сечения швов

Катет сварного шва k принимаем таким же как и при сварке элементов главной фермы .

Для автоматической сварки в нижнем положении диаметром проволоки от 1.4-х до 2 мм и катете шва от 3-х до 8 мм

Соединение раскоса с косынкой

Для раскоса выполненного из уголка №8 ГОСТ 8509-93 80х80х5,5 мм, длина лобового шва

Тогда из условия прочности можно вычислить длину флангового шва

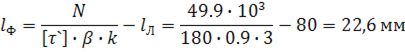
Не рекомендуется делать сварные швы длиной менее 30 мм. Поэтому принимаем

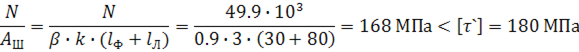
Соединение стойки с косынкой

Для стойки выполненной из уголка №5 50х50х4 ГОСТ 8509-93 длина лобового шва

Тогда из условия прочности можно вычислить длину флангового шва

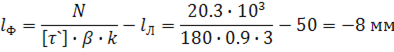
Не рекомендуется делать сварные швы длиной менее 30 мм. Поэтому принимаем

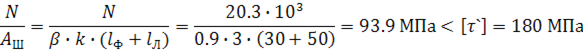
Расчет швов раскосов пространственной фермы

Определим максимальное допустимое усилие в раскосах:

Уголок №5.6, 56х56х4 с площадью поперечного сечения 438

Из условия устойчивости максимальное напряжение не должно превышать , где - из таблице СНиПа 72

Определим необходимую длину швов

фланговые швы не требуются, делаем их по каждый, как минимально допустимые.