Название: Расчет шарнирно-рычажных механизмов
Вид работы: курсовая работа
Рубрика: Промышленность и производство
Размер файла: 590.47 Kb
Скачать файл: referat.me-299587.docx
Краткое описание работы: 1. Структурный анализ главного механизма рис.1 1.1 Кинематическая схема главного механизма (рис. 1) По формуле Чебышева определим число степеней подвижности механизма:
Расчет шарнирно-рычажных механизмов
Расчет шарнирно-рычажных механизмов
1. Структурный анализ главного механизма
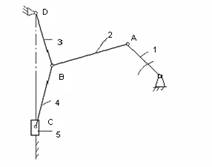
рис.1
1.1 Кинематическая схема главного механизма (рис. 1)
По формуле Чебышева определим число степеней подвижности механизма:
W = 3n-2p5 -p4 =3*5-2*7-0 = 1,
где 5 = n – число подвижных звеньев;
p5 =7 – число кинематических пар 5-го класса; 0= p4 –
число кинематических пар 4-го класса.
1.2 Построение структурной схемы механизма (рис. 2)
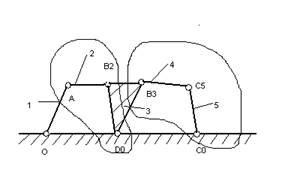
рис. 2
Выделим структурные группы (рис. 3):
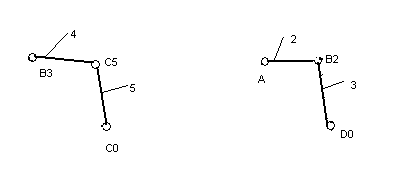
рис 3
группа из звеньев 4 и 5, первая в порядке образования механизма; группа из звеньев 2 и 3, вторая в порядке образования механизма; 1-й класс по Баранову; 2-й порядок. 2-й класс по Артоболевскому.
2. Кинематическое исследование главного механизма
2.1 Определение масштаба длин
Для построения планов положения механизма необходимо определить масштаб длин по формуле:
![]() м/мм,
м/мм,
где lOA = 0,044 м – истинная длина кривошипа (звено 1); 44 = ОА мм – отрезок, изображающий на кинематической схеме длину кривошипа (задан призвольно).
Длины отрезков на чертеже:
![]() мм;
мм;
![]() мм;
мм;
![]() мм;
мм;
![]() мм;
мм;
![]() мм;
мм;
![]() мм;
мм;
![]() мм;
мм;
![]() мм;
мм;
![]() мм.
мм.
2.2 Построение кинематической схемы главного механизма
В масштабе ![]() м/мм, строим кинематическую схему главного механизма в восьми положениях с общей точкой О, включая положения, где ползун 5 занимает крайнее верхнее и нижнее положения (прил. А, лист 1), разделив
м/мм, строим кинематическую схему главного механизма в восьми положениях с общей точкой О, включая положения, где ползун 5 занимает крайнее верхнее и нижнее положения (прил. А, лист 1), разделив
φрх =195о и φхх =165о на 4 части каждый.
2.3 Построение планов скоростей
Запишем векторные уравнения для построения планов скоростей структурных групп:
а ) группа 2 – 3
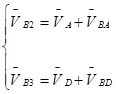
(2.1)![]()
где VD =0, так как точка неподвижна,
VА
=ω1*
lОА
=6,385*
0,044=0,28094 м/с, VВА
⊥ВA, VВ
D
⊥ВD, VВ3
=VВ2
, ω1
=![]() =
=![]() =6,385 с-1
=6,385 с-1
Масштабный коэффициент для построения планов скоростей определяем по формуле:
![]() м/с*
мм,
м/с*
мм,
где 40 мм – отрезок, изображающий на плане скоростей величину скорости т.А (задан призвольно).
Из плана скоростей находим:
![]() м/с;
м/с;
![]() м/с;
м/с;
![]() м/с;
м/с;
![]() м/с;
м/с;
![]() с-1
;
с-1
;
![]() с-1
;
с-1
;
Длины отрезков as2 и ds3 на планах скоростей находим из пропорций:
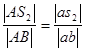 ;
; 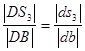 ;
;
б) группа 4 – 5
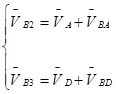
![]()
(2.2)
где VC 0 =0, V5-0 ׀׀у, VCB ⊥СВ.
Из плана скоростей находим:
![]() , м/с;
, м/с;
![]() , м/с;
, м/с;
![]() , с-1
;
, с-1
;
![]() м/с;
м/с;
Длину отрезка bs4 на планах скоростей находим из пропорции:
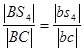 .
.
Результаты вычислений сводим в таблицу 1
Таблица 1
Положе ние |
Рабочий ход | |||||||||
| VBA | VBD | ω2 | ω3 | VS2 | VS3 | ω4 | VS4 | V5-0 | VCB | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0,3255 | 0,182 | 1,904 | 1,04 | 0,203 | 0,0917 | 1,04 | 0,175 | 0,21 | 0,182 |
| 2 | 0,147 | 0,238 | 0,86 | 1,36 | 0,266 | 0,13728 | 1,36 | 0,21 | 0,105 | 0,266 |
| 3 | 0,147 | 0,2744 | 0,86 | 1,568 | 0,2625 | 0,138 | 1,56 | 0,1435 | 0,105 | 0,238 |
| Холостой ход | ||||||||||
| 4 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 5 | 0,245 | 0,231 | 1,433 | 1,32 | 0,2436 | 0,11616 | 1,312 | 0,1316 | 0,0875 | 0,2296 |
| 6 | 0,147 | 0,3395 | 0,86 | 1,94 | 0,2905 | 0,17072 | 1,92 | 0,2485 | 0,252 | 0,336 |
| 7 | 0,0315 | 0,2555 | 0,184 | 1,46 | 0,2065 | 0,12672 | 1,44 | 0,2345 | 0,28 | 0,252 |
2.3. Построение планов ускорений.
Запишем векторные уравнения для построения плана ускорений структурных групп для положения №3 механизма:
а)группа 2 – 3
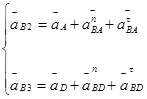
![]()
(2.3)
где аD
=0, так как точка D неподвижна, ![]() м/с2
,
м/с2
, ![]() м/с2
,
м/с2
, ![]() м/с2
,
м/с2
, ![]() ,
, ![]() .
.
Масштабный коэффициент для построения плана ускорений определяем по формуле:
![]() м/с2
*
мм,
м/с2
*
мм,
где 60 мм – отрезок, изображающий на плане ускорений величину ускорения т.А (задан призвольно).
Длины отрезков на плане ускорений:
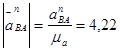 мм,
мм,
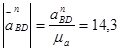 мм.
мм.
Из плана ускорений находим:
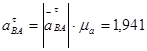 м/с2
м/с2
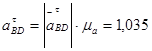 м/с2
м/с2
![]() м/с2
м/с2
![]() м/с2
м/с2
![]() м/с2
.
м/с2
.
Длины отрезков as2 и ds3 на планах скоростей находим из пропорций:
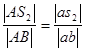 ;
; 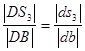 ;
;
Угловые ускорения звеньев определяем по формулам:
![]() с-2
;
с-2
;
![]() с-2
;
с-2
;
б)группа 4 – 5
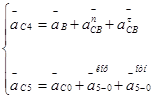
где аС0
=0, так как точка С0
неподвижна; ![]() , так как звено 5 совершает поступательное движение, ω5
=0
, так как звено 5 совершает поступательное движение, ω5
=0
![]() м/с2
;
м/с2
; ![]() ,
, ![]() .
.
Длины отрезков на плане ускорений:
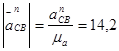 мм.
мм.
Из плана ускорений находим:
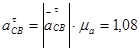 м/с2
м/с2
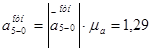 м/с2
м/с2
![]() м/с2
.
м/с2
.
Длину отрезка bs4 на плане ускорений находим из пропорции:
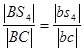 .
.
Угловое ускорение звена 4 определяем по формуле:
![]() с-2
;
с-2
;
3. АНАЛИЗ И СИНТЕЗ ЗУБЧАТОГО МЕХАНИЗМА
3.1 Кинематическая схема зубчатой передачи
Исходные данные:
![]()
3.2 Общее передаточное отношение зубчатой передачи
Определим общее передаточное отношение зубчатой передачи и число зубьев ![]() .
.
![]()
где 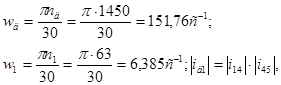
где 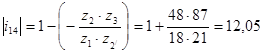 -
-
передаточное отношение планетарного механизма;
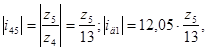
отсюда ![]() ,
,
округляем до целого ![]()
Проверим для планетарной передачи условия:
· соосности: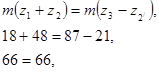
· соседства: ![]()
где![]() – число блоков саттелитов (задаётся);
– число блоков саттелитов (задаётся); ![]() - коэффициент высоты головки зуба.
- коэффициент высоты головки зуба.
![]()
![]()
· сборки: ![]()
где Q – любое целое число; L – наименьший общий делитель чисел ![]() и
и ![]() , в моём случае L=3.
, в моём случае L=3.
![]()
Условие сборки выполняется.
3.3 Синтез зубчатого зацепления
Зубчатое зацепление состоит из колёс ![]() Считаем, что зубчатые колёса – прямозубые эвольвентные цилиндрические, нарезанные стандартным реечным инструментом.
Считаем, что зубчатые колёса – прямозубые эвольвентные цилиндрические, нарезанные стандартным реечным инструментом.
3.3.1. Определяем:
· коэффициенты смещения реечного инструмента из условия устранения подреза:
для колеса ![]()
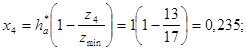
для колеса ![]()
![]() так как
так как ![]()
· угол эксплуатационного зацепления ![]()
![]()
По значению ![]() найдём угол
найдём угол ![]()
· коэффициент воспринимаемого смещения
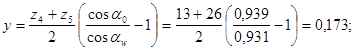
· коэффициент уравнительного смещения
![]()
· радиальный зазор
![]()
(![]() - коэффициент радиального зазора);
- коэффициент радиального зазора);
· межосевое расстояние
![]()
· радиусы делительных окружностей
![]()
![]()
· радиусы основных окружностей
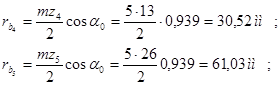
· радиусы начальных окружностей
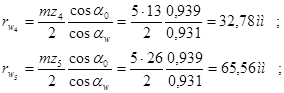
(проверка: ![]()
![]()
![]() );
);
· радиусы окружностей впадин
![]()
![]()
где ![]() - коэффициент высоты головки;
- коэффициент высоты головки;
· радиусы окружностей вершин
![]()
![]()
проверка:![]()
![]()
· толщину зубьев по делительной окружности
![]()
![]()
· шаг зацепления по делительной окружности
![]()
3.3.2. Расчёт значений коэффициентов относительного удельного скольжения зубьев произведён по формулам:
![]()
![]()
где ![]()
![]()
![]() и
и ![]() - отрезки, взятые по линии зацепления от точек
- отрезки, взятые по линии зацепления от точек ![]() и
и ![]() соответственно;
соответственно; ![]() .
.
Результаты расчётов сведены в таблицу.
| 0 | 30,75 | 61,5 | 92,25 | 123 | 164 | 205 | 246 | 287 | 328 | 369 | |
| -4,5 | -1,5 | -0,5 | 0 | 0,375 | 0,6 | 0,75 | 0,857 | 0,9375 | 1 | ||
| 1,0 | 0,815 | 0,6 | 0,333 | 0 | -0,6 | -1,5 | -3 | -6 | -15 |
По полученным значениям ![]() и
и ![]() построены графики изменения
построены графики изменения ![]() и
и ![]() .
.
3.3.3. Коэффициент перекрытия
![]()
где (ab) – длина активной части линии зацепления.
4. Силовой расчет главного механизма
Силовой расчет проведен для положения механизма №3(лист 3).
группа 4 – 5
• силы тяжести звеньев:
G4 = m4* g=353,16 Н;
G5 = m5* g=392,4 Н;
• силу производственного сопротивления по графику (лист 1):
Рпс =7000 Н;
• силы и моменты сил инерции звеньев:
![]() = m4*
аs
4
=38,34 Н;
= m4*
аs
4
=38,34 Н;
![]() = m5*
аs
5
=51,6 Н;
= m5*
аs
5
=51,6 Н;
![]() Н/м;
Н/м;
1) ![]() -? ,
-? ,![]()
![]() ;
;
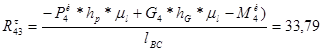 Н;
Н;
2) ![]() -? ,
-? , ![]() -? ,
-? , ![]()
![]() ;
;
Масштабный коэффициент для построения плана сил определяем по формуле:
![]() Н/мм;
Н/мм;
Длины отрезков на чертеже:
![]() мм;
мм;
![]() мм;
мм;
![]() мм – пренебрегаем;
мм – пренебрегаем;
![]() мм – пренебрегаем;
мм – пренебрегаем;
![]() мм – пренебрегаем;
мм – пренебрегаем;
Из плана сил находим:
![]() Н;
Н;
![]() Н;
Н;
![]() Н;
Н;
3) ![]() -? ,
-? , ![]()
![]() ;
;
Из плана сил находим:
![]() Н;
Н;
4)![]() ;
;
группа 2 – 3
• силы тяжести звеньев:
G2 = m2* g=196,2 Н;
G3 = m3* g=343,35 Н;
• силы и моменты сил инерции звеньев:
![]() = m2*
аs
2
=27 Н;
= m2*
аs
2
=27 Н;
![]() = m3*
аs
3
=19,53 Н;
= m3*
аs
3
=19,53 Н;
![]() Н/м;
Н/м;
![]() Н/м;
Н/м;
![]() Н;
Н;
1) ![]() -? ,
-? ,![]()
![]() ;
;
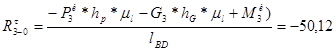 Н;
Н;
![]() необходимо перенаправить;
необходимо перенаправить;
2) ![]() -? ,
-? ,![]()
![]() ;
;
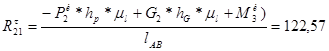 Н;
Н;
3) ![]() -? ,
-? , ![]() -? ,
-? , ![]()
![]() ;
;
Масштабный коэффициент для построения плана сил определяем по формуле:
![]() Н/мм;
Н/мм;
Длины отрезков на чертеже:
![]() мм;
мм;
![]() мм;
мм;
![]() мм – пренебрегаем;
мм – пренебрегаем;
![]() мм – пренебрегаем;
мм – пренебрегаем;
![]() мм – пренебрегаем;
мм – пренебрегаем;
![]() мм;
мм;
![]() мм – пренебрегаем;
мм – пренебрегаем;
![]() мм;
мм;
Из плана сил находим:
![]() Н;
Н;
![]() Н;
Н;
![]() Н;
Н;
начальное звено
1) Рур
-? ![]()
![]() ;
;
![]() Н;
Н;
![]() Н;
Н;
2) ![]()
![]()
Масштабный коэффициент для построения плана сил определяем по формуле:
![]() Н/мм;
Н/мм;
Длины отрезков на чертеже:
![]() мм;
мм;
![]() мм;
мм;
Из плана сил находим:
![]() Н;
Н;
![]() Н/м;
Н/м;
проверка
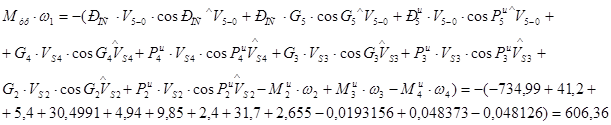
![]() Нм;
Нм;
Погрешность силового расчета составляет:
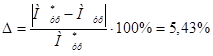 .
.
5. Силовой расчет с учетом сил трения
Выполнен на листе 3. Все масштабные коэффициенты сил совпадают с масштабными коэффициентами сил на силовом расчете без учета сил трения.
Определяем силы и моменты трения
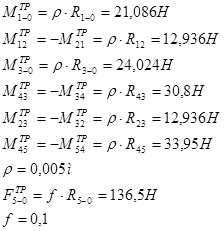
группа 4-5
1) ![]() -? ,
-? ,![]()
![]() ;
;
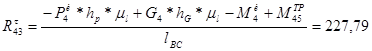 Н;
Н;
2)![]()
из плана сил находим ![]()
группа 2-3
1) ![]() -? ,
-? ,![]()
![]() ;
;
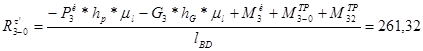 Н;
Н;
2) ![]() -? ,
-? ,![]()
![]() ;
;
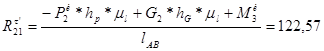 Н;
Н;
из плана сил находим ![]()
начальное звено
![]() ;
;
![]() Н;
Н;
КПД главного механизма равен:
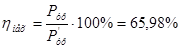
6. Выбор электродвигателя
Определяем работу сил полезного сопротивления
Определяем работу сил полезного сопротивления ![]() на интеревале одного оборота главного вала (начального звена). Эта работа определяется как площадь
на интеревале одного оборота главного вала (начального звена). Эта работа определяется как площадь ![]() , ограниченная графиком
, ограниченная графиком ![]() и осью абсцисс, умноженная на масштабы
и осью абсцисс, умноженная на масштабы ![]() и
и ![]() :
:
![]()
![]()
6.1 Определяем требуемую мощность приводного электродвигателя
![]()
где Т – время одного оборота главного вала, с; ![]() ;
; ![]() - КПД зубчатой передачи (принимаем
- КПД зубчатой передачи (принимаем ![]() );
); ![]() - КПД главного механизма (
- КПД главного механизма (![]() .
.
6.2 Выбор электродвигателя по каталогу
По каталогу асинхронных электродвигателей выбираем асинхронный электродвигатель 4АА63В4У3.
![]() - мощность электродвигателя;
- мощность электродвигателя; ![]() - синхронное число оборотов;
- синхронное число оборотов; ![]() - номинальное число оборотов;
- номинальное число оборотов; ![]() - момент инерции ротора электродвигателя.
- момент инерции ротора электродвигателя.
6.3 Определение приведенного момента сил
Приведенный момент сил тяжести и сил полезных сопротивлений рассчитываются для всех рассматриваемых положений механизма по формуле:
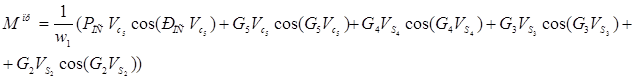
По результатам расчёта строим график ![]() .
.
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| 0 | 0 | 14,1489 | 7000 | 7000 | 0 | 0 | 0 | 0 | |
| 0 | 0,21 | 0,105 | 0,105 | 0 | 0,0875 | 0,252 | 0,28 | 0 | |
| - | 180 | 180 | 180 | - | 0 | 0 | 0 | - | |
| - | -1 | -1 | -1 | 1 | 1 | 1 | - | ||
| - | 0 | 0 | 0 | - | 180 | 180 | 180 | - | |
| - | 1 | 1 | 1 | - | -1 | -1 | -1 | - | |
| 0 | 0,175 | 0,21 | 0,1435 | 0 | 0,1316 | 0,2485 | 0,2345 | 0 | |
| - | 25 | 35 | 56 | - | 120,5 | 140,5 | 162 | - | |
| - | 0,9063 | 0,81915 | 0,55915 | - | -0,50754 | -0,77162 | -0,95106 | - | |
| 0 | 0,0917 | 0,13728 | 0,138 | 0 | 0,11616 | 0,17072 | 0,12672 | 0 | |
| - | 55 | 64 | 77 | - | 102 | 112,5 | 124 | - | |
| - | 0,57358 | 0,43837 | 0,22495 | - | -0,2079 | -0,38268 | -,5592 | - | |
| 0 | 0,203 | 0,266 | 0,2625 | 0 | 0,2436 | 0,2905 | 0,2065 | 0 | |
| - | 127 | 86 | 52 | - | 58 | 95,5 | 127 | - | |
| - | -0,60182 | 0,06976 | 0,61566 | - | 0,52992 | -0,09585 | -0,60182 | - | |
| 0 | 20,753 | -7,9165 | -97,587 | 0 | -6,4038 | -30,46 | -37,173 | 0 |
Углы между векторами сил и скоростей точек их приложения замерены на планах скоростей.
6.4 Определение приведенного момента инерции
Приведенный момент инерции ![]() определяем из условия равенства в каждый момент времени кинетической энергии модели кинетической энергии машинного агрегата.
определяем из условия равенства в каждый момент времени кинетической энергии модели кинетической энергии машинного агрегата.
Приведенный момент инерции рычажного механизма ![]() рассчитан по формуле:
рассчитан по формуле:
![]()
| № полож. | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 0 | 0,0982 | 0,101 | 0,5095 | 0 | 0,0638 | 0,178 | 0,1607 | 0 |
6.5 Суммарный приведенный момент инерции агрегата
Суммарный приведенный момент инерции агрегата равен сумме трёх слагаемых
![]()
где ![]() - приведенный момент инерции ротора электродвигателя,
- приведенный момент инерции ротора электродвигателя, ![]() :
:
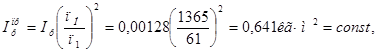
(![]() - осевой момент инерции ротора, взятый из каталога электродвигателя);
- осевой момент инерции ротора, взятый из каталога электродвигателя);
![]() - приведенный момент инерции зубчатых колёс редуктора и пары
- приведенный момент инерции зубчатых колёс редуктора и пары ![]() :
:
![]()
где ![]() - момент инерции зубчатых колёс редуктора относительно своих осей, кг*с2
;
- момент инерции зубчатых колёс редуктора относительно своих осей, кг*с2
; ![]() - массы зубчатых колёс
- массы зубчатых колёс ![]() ;
; ![]() - скорость оси сателлитов,м/с;
- скорость оси сателлитов,м/с; ![]() - угловая скорость сателиттов, с-1
;
- угловая скорость сателиттов, с-1
; ![]() - угловая скорость вала двигателя, с-1
;
- угловая скорость вала двигателя, с-1
; ![]() - угловая скорость i-го зубчатого колеса, с-1
; к – число блоков сателиттов (принимаем к=3).
- угловая скорость i-го зубчатого колеса, с-1
; к – число блоков сателиттов (принимаем к=3).
Момент инерции зубчатых колёс вычисляем по формуле
![]()
где ![]() - масса i – го зубчатого колеса равна
- масса i – го зубчатого колеса равна
![]()
(b=0,05 м – ширина венца зубчатого колеса; ![]() - удельный вес стали),
- удельный вес стали), ![]() - радиус делительной окружности (m = 5мм):
- радиус делительной окружности (m = 5мм):
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Скорость оси сателлита
![]()
где ![]()
Угловая скорость блока сателлитов ![]() определена с использованием метода инверсии:
определена с использованием метода инверсии:
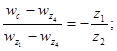
![]()
откуда ![]() .
.
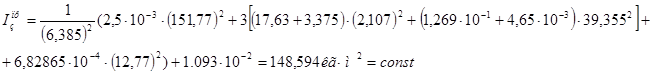
6.6 Исследование установившегося движения
Предполагаем, что приведенный момент двигателя
![]() на рабочем участке механической характеристики электродвигателя можно описать параболой
на рабочем участке механической характеристики электродвигателя можно описать параболой ![]() , где А и В – некоторые постоянные величины, которые определим по формулам:
, где А и В – некоторые постоянные величины, которые определим по формулам:
![]() ;
;
![]() ;
;
где ![]() - приведенный к звену 1 номинальный момент на роторе электродвигателя;
- приведенный к звену 1 номинальный момент на роторе электродвигателя;
![]() - приведенная к звену 1 синхронная угловая скорость электродвигателя;
- приведенная к звену 1 синхронная угловая скорость электродвигателя;
![]() - приведенная к звену 1 номинальная угловая скорость электродвигателя;
- приведенная к звену 1 номинальная угловая скорость электродвигателя;
6.7 Определяем закон движения звена 1
Определяем закон движения звена 1 ![]() , используя формулу:
, используя формулу:
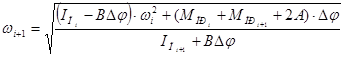 ;
;
где i=1,2,…12 – индекс соответствует номеру положения кривошипа;
![]() - угловой шаг.
- угловой шаг.
Задавшись ![]() с-1
, последовательно ведем расчет для i=1,2,…12. Результаты расчетов представлены в табл. 9. Значения
с-1
, последовательно ведем расчет для i=1,2,…12. Результаты расчетов представлены в табл. 9. Значения ![]() и
и ![]() взяты из табл. 7 и табл. 8.
взяты из табл. 7 и табл. 8.
Искомые значения ω1
выделены в табл. 9. По этим значениям построен график зависимости ![]() (лист 3).
(лист 3).
По табл. 9 определяем
![]() с-1
;
с-1
; ![]() с-1
;
с-1
;
![]() с-1
;
с-1
;
Коэффициент неравномерности хода машины
![]() .
.
Таблица 9.
| i п/п | |||
| 1 | 149,305 | 15,5 | 6,385 |
| 2 | 149,335 | 19 | 6,394 |
| 3 | 149,385 | 2 | 6,398 |
| 4 | 149,465 | -47 | 6,385 |
| 5 | 149,715 | -97 | 6,34 |
| 6 | 149,345 | -34 | 6,312 |
| 7 | 149,245 | -1,5 | 6,304 |
| 8 | 149,305 | -7 | 6,3 |
| 9 | 149,39 | -26 | 6,289 |
| 10 | 149,41 | -35 | 6,267 |
| 11 | 149,365 | -32 | 6,249 |
| 12 | 149,235 | 0 | 6,243 |
7. Синтез кулачкового механизма
7.1 Определение закона движения толкателя
Исходные данные: закон движения толкателя
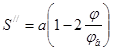
где h
= 0,052 мм – ход толкателя; фазовые углы: ![]()
![]() - допустимый угол давления.
- допустимый угол давления.
Дважды аналитически проинтегрируем закон движения толкателя.
![]()
Начальные условия: при ![]()
Следовательно, ![]()
![]()
![]()
При ![]()
![]()
![]()
![]()
Определим параметр а
из условия: ![]()
![]()
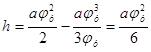
![]()
Подсчитанные значения ![]() на интервале удаления с шагом
на интервале удаления с шагом ![]() приведены в таблице.
приведены в таблице.
| 0 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | |
| 0,2092 | 0,1497 | 0,0897 | 0,0299 | -0,0299 | -0,0897 | -0,1497 | -0,2092 | |
| 0 | 0,0313 | 0,05214 | 0,0625 | 0,0625 | 0,05214 | 0,0313 | 0 | |
| 0 | 0,0029 | 0,01031 | 0,02047 | 0,03153 | 0,04169 | 0,04912 | 0,052 |
При ![]() :
:
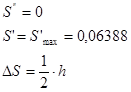
Масштабные коэффициенты: ![]()
![]()
Строим теоретический профиль кулачка, пользуясь методом инверсии. Радиус ролика ![]() .
.
7.2 Определение жёсткости замыкающей пружины
Определяем жёсткость замыкающей пружины и усилие предварительного сжатия из условия
![]() ,
,
где ![]() - усилие предварительного сжатия пружины, Н;
- усилие предварительного сжатия пружины, Н; ![]() - масса толкателя;
- масса толкателя; ![]() - угловая скорость кулачка;
- угловая скорость кулачка; ![]() - аналог ускорения толкателя, м.
- аналог ускорения толкателя, м.
Для этого строим график ![]() , проводим из начала координат касательную к графику, а затем прямую, ей параллельную, на расстоянии
, проводим из начала координат касательную к графику, а затем прямую, ей параллельную, на расстоянии ![]() .(
.(![]() - ускорение толкателя, соответствующее точке касания М).
- ускорение толкателя, соответствующее точке касания М).
Получим график для определения характеристик пружины.
Жёсткость пружины:
![]()
СПИСОК ЛИТЕРАТУРЫ
1 Волгов В.А. Детали и узлы РЭА. –М.: Энергия. 2001. –656 с.
2 Устройства функциональной радиоэлектроники и электрорадиоэлементы: Конспект лекций. Часть I / М.Н. Мальков, В.Н. Свитенко. – Харьков:ХИРЭ. 2002. – 140 с.
3 Справочник конструктора РЭА: Общие принципы конструирования/ Под редакцией Р.Г. Варламова. – М.: Сов. Радио. 1999. – 480 с.
4 Фрумкин Г.Д. Расчет и конструирование радиоаппаратуры. – М.: Высшая школа. 1999. – 339 с.
Похожие работы
-
Принцип качающегося стола
СОДЕРЖАНИЕ 1. Введение .............................................................................................................4
-
Структурный анализ механизма
Введение Структурный анализ механизма Кинематический анализ механизма методом планов Кинематический анализ механизма методом планов скоростей Кинематический анализ механизма методом планов ускорений
-
Кинематический и силовой расчет механизма долбежного станка с качающейся кулисой
Структурный анализ, построение положений механизма и планов скоростей для рабочего и холостого хода, верхнего и нижнего крайних положений. Построение планов ускорений, кинетостатический расчет механизма. Определение сил инерции и сил тяжести звеньев.
-
Кинематический и силовой анализ рычажного механизма
Министерство образования и науки Российской Федерации Федеральное агентство по образованию Государственное образовательное учреждение Высшего профессионального образования
-
Кинематическое и кинетостатическое исследование рычажного механизма
Структурный анализ рычажного механизма. Кинематическое исследование рычажного механизма графо-аналитическим методом. Определение скоростей и ускорений шарнирных точек, центров тяжести звеньев и угловых скоростей звеньев. Силовой расчёт устройства.
-
Анализ нагруженности плоского рычажного механизма
Структурный, динамический и кинетостатический анализ плоского рычажного механизма. Определение угловых скоростей его звеньев; внешних сил и моментов инерции, действующих на каждое звено и кинематическую пару. Проектный расчет механизма на прочность.
-
Механизм долбежного станка с качающейся кулисой
Структурный анализ механизма, построение его положений. Определение уравновешивающей силы с помощью рычага Жуковского. План скоростей и ускорений для рабочего и холостого хода, верхнего и нижнего положений. Определение сил инерции и сил тяжести звеньев.
-
Структурный и кинематический анализ рычажного механизма
Кинематическая схема шарнирного механизма. Определение длины кулисы и масштабного коэффициента длины. Построение плана положения механизма для заданного положения кривошипа методом засечек. Построение плана скоростей. Расчет углового ускорения кулисы.
-
Рычажный и кулачковый механизм
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ НОВГОРОДСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИМЕНИ ЯРОСЛАВА МУДРОГО ____________________________________________________________________________________________
-
Структурный анализ механизмов
Основные понятия и определения в теории механизмов. Кинематические пары, их главные свойства и классификация. Кинематические цепи: сущность и разновидности. Степень подвижности плоской кинематической цепи. Структурная классификация плоских механизмов.