Название: Расчет конического редуктора
Вид работы: дипломная работа
Рубрика: Промышленность и производство
Размер файла: 343.41 Kb
Скачать файл: referat.me-300191.docx
Краткое описание работы: Кинематический и силовой анализ привода, выбор электродвигателя, передаточных отношений для редуктора и цепной передачи. Выбор материалов и допускаемых напряжений для зубчатых колес. Расчет конической прямозубой передачи, определение усилий в зацеплении.
Расчет конического редуктора
Кинематический и силовой анализ привода
Выбор электродвигателя
1. Требуемая мощность электродвигателя:
![]()
Где: 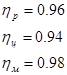
2. Частота вращения Приводного вала:
![]()
Выбираем значения передаточных отношений для редуктора и цепной передачи
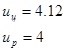
Требуемая частота вращения двигателя:
![]()
В соответствии с ГОСТ 19523-81 выбираем электродвигатель АИР160S8/727
, мощностью ![]() и частотой вращения
и частотой вращения ![]() .
.
3. Передаточные числа звеньев:
![]()
Полученное передаточное число распределяют между типами передач.
Сохраняя выбранные значения передач 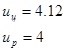 , получим:
, получим:
![]()
Передаточные числа согласуются со стандартными значениями согласно ГОСТ 2185-66
Отклонение от стандартного значения не должно превышать ![]()
![]()
4. Частоты вращения и крутящие моменты на валах:
- Частота вращения на быстроходном валу редуктора
![]()
- Частота вращения на тихоходном валу редуктора
![]()
- Момент на приводном валу
![]()
- Момент на тихоходном валу редуктора
![]()
- Момент на быстроходном валу редуктора
![]()
- Момент на валу электродвигателя
![]()
С другой стороны
![]()
Выбор материалов и допускаемых напряжений
Расчет допускаемых напряжений для зубчатых колес
Вследствие того, что производство мелкосерийное выбираем Сталь марки Ст40Х, вид термообработки – улучшение, ![]() .
.
Примем:
для шестерни НB1 = 350
для колеса на 20…30 HB меньше – HB2 = 330.
1. Допускаемые контактные напряжения
1. Для шестерни:
![]() ,
,
где ![]() - коэффициент запаса (безопасности),
- коэффициент запаса (безопасности), ![]() - коэффициент долговечности.
- коэффициент долговечности.
![]()
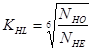 . Коэффициент долговечности изменяется в пределах
. Коэффициент долговечности изменяется в пределах ![]() .
.
Базовое число циклов ![]()
Эквивалентное число циклов нагружения
![]() ,
,
где ![]() - частота вращения колеса
- частота вращения колеса ![]() ,
, ![]() - расчетный ресурс редуктора
- расчетный ресурс редуктора ![]() ,
, ![]() - относительно значение крутящего момента на i – той ступени графика нагрузки,
- относительно значение крутящего момента на i – той ступени графика нагрузки, ![]() - относительная продолжительность действия крутящего момента на i – той ступени графика нагрузки, L – срок службы,
- относительная продолжительность действия крутящего момента на i – той ступени графика нагрузки, L – срок службы,
![]() ,
, ![]() ,
,![]() - годовой и суточный коэффициенты, t – расчетный ресурс редуктора.
- годовой и суточный коэффициенты, t – расчетный ресурс редуктора.
![]()
![]()
Так как ![]() >
> ![]() , то
, то ![]()
![]() ,
, ![]()
![]() часов.
часов.
Тогда ![]()
2. Определяем допускаемы контактные напряжения на колесе:
![]()
![]()
![]()
![]()
Так как ![]() >
> ![]() , то
, то ![]() ,
, ![]() , тогда
, тогда
![]()
Расчетные допускаемые контактные напряжения:
![]()
Что не превышает предельного значения ![]() :
:
![]() - для прямозубой передачи.
- для прямозубой передачи.
Допускаемые контактные напряжения при перегрузке:
![]()
2. Расчет допускаемых изгибных напряжений
Допускаемые напряжения изгиба определяются:
Для шестерни
![]() ,
,
где предел выносливости ![]() и коэффициент запаса
и коэффициент запаса ![]() определяют из таблицы:
определяют из таблицы:
![]() - при нереверсируемой передаче.
- при нереверсируемой передаче.
![]() при H < 350 HB.
при H < 350 HB.
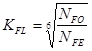 при H < 350 HB, где
при H < 350 HB, где ![]() ,
,
![]()
Выбираем:
![]()
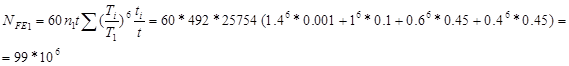
![]()
Так как ![]() , то
, то ![]() , следовательно:
, следовательно:
![]()
Для колеса
![]()
![]()
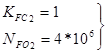 так как нереверсивная нагрузка.
так как нереверсивная нагрузка.
Так как ![]() , то
, то ![]() , следовательно:
, следовательно:
![]()
Допускаемые изгибные напряжения при перегрузке:
![]()
Геометрические характеристики зацепления
Исходные данные:
Крутящий момент на колесе ![]()
Частота вращения колеса ![]()
Передаточное отношение ![]()
Расчетные допускаемые контактные напряжения ![]()
Проектный расчет конической прямозубой передачи
1. Диаметр внешней делительной окружности колеса:
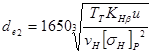 ,
,
где ![]() - коэффициент, учитывающий концентрацию нагрузки по длине зуба; при консольном расположении шестерниориентировочно принимают
- коэффициент, учитывающий концентрацию нагрузки по длине зуба; при консольном расположении шестерниориентировочно принимают![]()
![]() - эмпирический коэффициент для прямозубых колес.
- эмпирический коэффициент для прямозубых колес.
Принимаем ![]() .
.
![]() При
При![]() и
и![]() по ГОСТ 12289-76 имеем ширину колеса
по ГОСТ 12289-76 имеем ширину колеса
![]()
2. Число зубьев шестерни
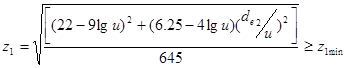
![]()
Где ![]() .
.
Угол вершине делительного конуса шестерни:
![]()
![]()
Принимаем ![]() зубьев.
зубьев.
3. Число зубьев колеса
![]()
![]()
4. Фактическое передаточное число
![]()
Относительная погрешность ![]()
Относительная погрешность должна составлять не более 4%.
![]()
5. Определяем максимальный (производственный) окружной и нормальный модули прямозубых колес:
![]()
Модуль конических передач можно не согласовывать со стандартным значением
Диаметр внешней делительной окружности:
![]()
6. Внешнее конусное расстояние:
![]()
7. Уточняем коэффициент ширины зубчатого венца:
![]()
![]()
Коэффициент ширины зубчатого венца находится в рекомендуемых стандартом пределах:
![]()
8. Среднее конусное расстояние
![]()
9. Средний окружной и нормальный модули:
![]()
10. Средние делительные диаметры:
Шестерни
![]()
Колеса
![]()
Проверочный расчет прямозубой конической передачи
Проверочный расчет по контактным напряжениям
1. Условие прочности по контактным напряжениям для стальных колес:
![]()
Условие прочности: 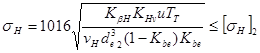
Где ![]() - коэффициент концентрации нагрузки находится из таблицы в зависимости от расположения шестерни и твердости колес. При
- коэффициент концентрации нагрузки находится из таблицы в зависимости от расположения шестерни и твердости колес. При ![]() для роликоподшипниковых колес
для роликоподшипниковых колес ![]()
![]() - коэффициент динамичности. Определяется в зависимости от степени точности и окружной скорости на среднем делительном диаметре.
- коэффициент динамичности. Определяется в зависимости от степени точности и окружной скорости на среднем делительном диаметре.
![]()
Назначаем степень точности: 8.
Для прямозубых колес выбираем коэффициент ![]() , условно принимая точность на одну степень ниже фактической (9-ю степень точности).
, условно принимая точность на одну степень ниже фактической (9-ю степень точности).
![]() для прямозубой передачи.
для прямозубой передачи.
Эмпирический коэффициент ![]()
Значение контактных напряжений:
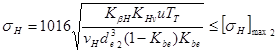
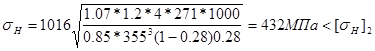
Недогрузка составляет:
![]()
Проверочный расчет по напряжениям изгиба.
1. Условие прочности по напряжениям изгиба для зубьев колеса:
![]()
Для шестерни: ![]()
Где ![]() - коэффициент концентрации нагрузки
- коэффициент концентрации нагрузки
![]() ,
,
где ![]() принимаем по таблице в зависимости от принятой схемы расположения колес.
принимаем по таблице в зависимости от принятой схемы расположения колес. ![]()
Коэффициент динамичности ![]()
Коэффициент формы зуба ![]() и
и ![]() определяют по таблице при эквивалентном числе зубьев
определяют по таблице при эквивалентном числе зубьев
![]()
![]() 4,07
4,07
![]()
Эмпирический коэффициент ![]()
Допускаемые напряжения: ![]()
Значения напряжений изгиба:
Колеса:
![]()
Шестерни:
![]()
2. Проверим зубья на прочность при пиковых перегрузках
Под пиковой перегрузкой понимается возникающий при пуске максимальный момент электродвигателя ![]() .
.
![]()
Проверяем на контактную прочность при пиковой перегрузке:
![]()
![]() <
< ![]()
Следовательно, местная пластическая деформация зубьев будет отсутствовать.
Проверка изгибной прочности при перегрузке:
![]() <
< ![]()
Геометрические характеристики зацепления
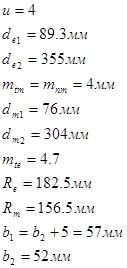
По ГОСТ 13754-81 исходный контур имеет параметры: ![]()
1. Высота головки зуба:
![]()
![]()
2. Высота ножки зуба в среднем сечении шестерни и колеса соответственно:
![]()
![]()
Внешняя высота ножки зуба:
![]()
![]()
3. Угол ножки зуба:
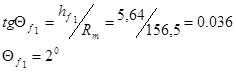
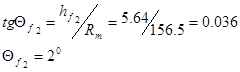
4. Угол головки зуба:
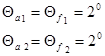
5. Угол конуса вершин:
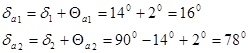
6. Угол конуса впадин:
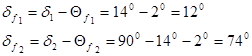
7. Внешний диаметр вершин зубьев:
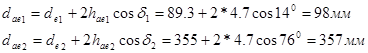
8. Внешний диаметр впадин зубьев:
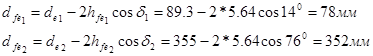
Определение усилий в зацеплении.
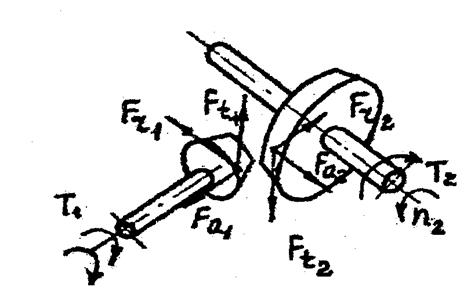
Окружная сила на среднем диаметре колеса:
![]()
Осевая сила на шестерне:
![]()
Радиальная сила на шестерне:
![]()
Расчет цепной передачи.
Мощность на малой звездочке:
![]()
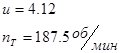
Равномерная спокойная нагрузка.
1. Назначаем число зубьев меньшей звездочки ![]() в зависимости от передаточного числа.
в зависимости от передаточного числа. ![]() при
при ![]() . Выбираем
. Выбираем ![]() при
при ![]()
2. Число зубьев большой звездочки:
![]() , принимаем нечетное число
, принимаем нечетное число ![]() .
.
3. Уточняем передаточное число:
![]()
![]()
4. Назначаем шаг цепи по условию ![]() , где
, где ![]() - наибольший рекомендуемый шаг цепи. Назначаем в зависимости от
- наибольший рекомендуемый шаг цепи. Назначаем в зависимости от
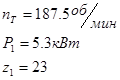
![]()
Принимаем ![]() .
.
5. Определяем среднюю скорость цепи.
![]()
6. Рассчитаем окружное усилие:
![]()
7. Найдем разрушающую нагрузку цепи:
![]() , где
, где ![]() - коэффициент динамической нагрузки, выбираемый в зависимости от характера нагрузки. При равномерной спокойной нагрузке
- коэффициент динамической нагрузки, выбираемый в зависимости от характера нагрузки. При равномерной спокойной нагрузке ![]() .
.
Допускаемый коэффициент запаса прочности для роликовых цепей:
![]()
![]() - натяжение цепи от действия центробежных сил на звездочках, где
- натяжение цепи от действия центробежных сил на звездочках, где ![]() - масса 1м. длины цепи, принимаемая по ГОСТ 13586-75.
- масса 1м. длины цепи, принимаемая по ГОСТ 13586-75. ![]() - средняя скорость цепи.
- средняя скорость цепи.
![]() - натяжение цепи от провисания холостой ветви, где
- натяжение цепи от провисания холостой ветви, где ![]() - коэффициент провисания, зависящий от угла наклона лини центров передач к горизонту и стрелы провисания цепи
- коэффициент провисания, зависящий от угла наклона лини центров передач к горизонту и стрелы провисания цепи ![]() .
.
При горизонтальном расположении линии центров передач ![]() .
. ![]() - межосевое расстояние,
- межосевое расстояние, ![]() .
.
Так как силы ![]() и
и ![]() малы по сравнению с силой
малы по сравнению с силой ![]() , то ими можно пренебречь. Тогда:
, то ими можно пренебречь. Тогда:
![]()
По ГОСТ 10947-64 выбираем цепь ПР-50,8-16000, [1. с.211] умеющую принятый шаг p = 50,8 и разрушающую нагрузку ![]() .
.
8. Проверяем давление в шарнирах цепи.
![]() ,
,
где ![]() - окружное усилие.
- окружное усилие. ![]() , А – проекция опорной поверхности шарнира цепи на диаметральную плоскость, мм2
.
, А – проекция опорной поверхности шарнира цепи на диаметральную плоскость, мм2
.
Для приводных роликовых цепей ![]() , где d – диаметр валика цепи. B – длина втулки шарнира цепи.
, где d – диаметр валика цепи. B – длина втулки шарнира цепи.
Для выбранной цепи ПР-50,8-16000:
![]() ,
, ![]()
![]()
Допускаемое давление ![]() , где
, где ![]() - допускаемое давление в шарнирах цепи, полученное при испытании типовых передач в средних условиях эксплуатации, принимают в зависимости от частоты вращения и шага цепи.
- допускаемое давление в шарнирах цепи, полученное при испытании типовых передач в средних условиях эксплуатации, принимают в зависимости от частоты вращения и шага цепи.
У нас ![]() .
.
![]() - коэффициент, учитывающий условия эксплуатации и типовых условий испытаний цепей.
- коэффициент, учитывающий условия эксплуатации и типовых условий испытаний цепей.
![]()
Где![]() - Коэффициент динамической нагрузки, при равномерной спокойной нагрузке
- Коэффициент динамической нагрузки, при равномерной спокойной нагрузке ![]() .
.
![]() - коэффициент межосевого расстояния.
- коэффициент межосевого расстояния.
![]() при
при ![]() .
.
![]()
![]() - коэффициент наклона передачи к горизонту.
- коэффициент наклона передачи к горизонту.
При ![]()
![]()
![]() - коэффициент регулировки передачи. Предполагая, что регулировка передачи производиться не будет
- коэффициент регулировки передачи. Предполагая, что регулировка передачи производиться не будет ![]()
![]() - коэффициент смазки.
- коэффициент смазки.
При периодической смазки цепи ![]()
Тогда ![]() ,
, ![]() находится в рекомендуемых пределах.
находится в рекомендуемых пределах.
Давление в шарнирах цепи:
![]()
![]()
Так как ![]() , оставляем цепь ПР-50,8-16000.
, оставляем цепь ПР-50,8-16000.
9. Определяем межосевое расстояние передачи.
Межосевое расстояние выбираем в пределах ![]() .
.
Принимаем ![]()
10. Длина цепи, выраженная в числах звеньев цепи.
![]()
Принимаем ![]() звена.
звена.
11. Для обеспечения долговечности цепи должно соблюдаться условие:
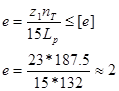
Где ![]() - число ударов цепи в секунду,
- число ударов цепи в секунду, ![]() - допускаемое число ударов в секунду, выбирается [2. c.255] в зависимости от шага цепи. У нас:
- допускаемое число ударов в секунду, выбирается [2. c.255] в зависимости от шага цепи. У нас:
![]()
![]() - условие долговечности соблюдается.
- условие долговечности соблюдается.
12. Уточняем межосевое расстояние
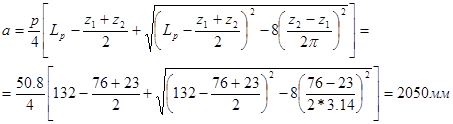
![]()
12. Оценим возможность резонансных колебаний цепи:![]()
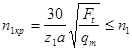
![]()
Где ![]() - частота вращения тихоходного вала редуктора,
- частота вращения тихоходного вала редуктора, ![]() - масса 1м. длины цепи.
- масса 1м. длины цепи.
![]()
Тогда ![]() ,
, ![]()
Следовательно, резонансные колебания будут отсутствовать.
14. Определяем нагрузку на валы передачи.
С достаточной степенью точности можно полагать, что нагрузка на вал направлена по линии центров передач и составляет ![]() , при
, при ![]() .
.
Имеем, ![]()
15. Диаметры делительных окружностей звездочек
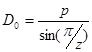
Отсюда:
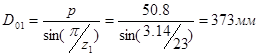
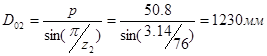
Звездочку на приводном валу (![]() ) конического редуктора крепим шпонкой со скругленными концами:
) конического редуктора крепим шпонкой со скругленными концами: 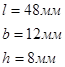 . Глубина паза на валу
. Глубина паза на валу ![]()
Подбор муфт.
Исходные данные:
Муфта упругая, передаваемый момент ![]() , режим работы нереверсивный, равномерный, спокойный. Поломка муфты приводит к аварии машины без человеческих жертв.
, режим работы нереверсивный, равномерный, спокойный. Поломка муфты приводит к аварии машины без человеческих жертв.
1. Расчетный момент муфты.
![]()
Где ![]() - номинальный момент на муфте.
- номинальный момент на муфте. ![]()
![]() - коэффициент режима работы.
- коэффициент режима работы.
![]() , где
, где ![]() - коэффициент безопасности.
- коэффициент безопасности. ![]() - учитывает характер нагрузки.
- учитывает характер нагрузки.
При условии того, что поломка муфты приводит к аварии машины без человеческих жертв ![]() .
.
При спокойной равномерной нагрузке ![]() .
.
Тогда ![]()
По ГОСТ 20884-93 примем упругую муфту с торообразной неразрезной оболочкой со следующими параметрами:
![]() ,
, ![]() , наружный диаметр муфты
, наружный диаметр муфты ![]() .
.
![]() 2. Определим силу, действующую со стороны муфты на вал.
2. Определим силу, действующую со стороны муфты на вал.
![]()
![]() Окружная сила на муфте:
Окружная сила на муфте:
![]()
Примем ![]()
3. Проверяем возможность посадки муфты на вал редуктора.
Расчетный диаметр в месте посадки
![]() , где
, где ![]() ,
,
где с достаточной точностью можно пренебречь величиной ![]() , и тогда
, и тогда ![]()
Допускаемые напряжения
![]()
![]()
С учетом ослабления вала шпоночной канавкой:
![]() , что меньше посадочного диаметра муфты
, что меньше посадочного диаметра муфты ![]() , следовательно, данная муфта проходит по посадочному диаметру вала и в дальнейшем диаметр вала под муфту принимается
, следовательно, данная муфта проходит по посадочному диаметру вала и в дальнейшем диаметр вала под муфту принимается ![]()
Муфта на быстроходном валу редуктора крепится шпонкой со скругленными концами:. Глубина паза на валу ![]()
Расчет валов. [4. с. 259]
Исходные данные:
![]()
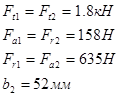
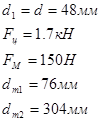
Проектный расчет быстроходного вала.
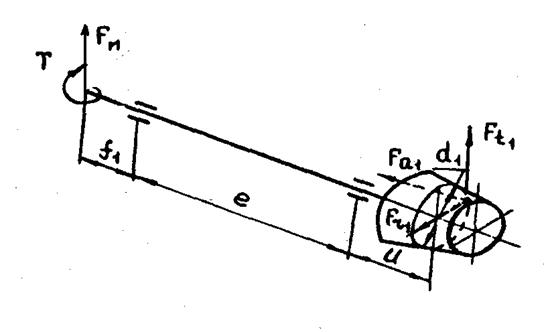
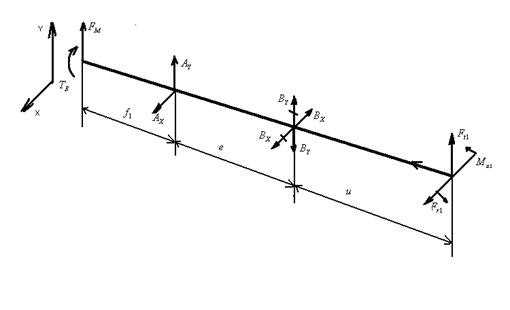
1. Ориентировочно назначаем длины участков вала:
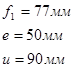
Согласно расчетной схеме определяем реакции опор в горизонтальной плоскости из условия равновесия:
![]()
Тогда:
![]()
Где ![]()
![]()
Знак минус означает, что реакция в опоре «В» направлена в противоположную сторону.
Аналогично:
![]()
![]()
![]()
Условие равновесия проекций на ось «X»:
![]()
![]()
Следовательно:
![]()
2. Реакции опор в вертикальной плоскости:
![]()
![]()
Знак «минус» говорит о том, что реакция направлена в противоположную сторону.
![]()
![]()
Условие равновесия проекций на ось «Y»:
![]()
Следовательно:
![]()
3. Радиальная нагрузка на опору «А»:
![]()
Радиальная нагрузка на опору «B»:
![]()
4. Изгибающие моменты в характерных сечениях вала:
- в горизонтальной плоскости для среднего сечения шестерни:
![]()
- под подшипником «В»:
![]()
![]()
- на муфте
![]()
- под подшипником «А»:
![]()
![]()
Проверка:
![]()
![]()
Следовательно, моменты найдены правильно.
5. Определяем диаметры вала по зависимости:
![]() , где
, где ![]() ;
;
![]() - эквивалентный момент;
- эквивалентный момент; ![]() - суммарный изгибающий момент;
- суммарный изгибающий момент; ![]() - крутящий момент.
- крутящий момент.
![]() ,
,
где ![]() - изгибающие моменты в горизонтальной и вертикальной плоскостях соответственно.
- изгибающие моменты в горизонтальной и вертикальной плоскостях соответственно.
Для обеспечения достаточной жесткости вала рекомендуется принимать ![]() в зависимости от материала и диаметра. Принимаем
в зависимости от материала и диаметра. Принимаем![]()
6. Определяем расчетный диаметр вала под шестерней.
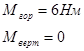
![]()
![]()
![]()
![]()
Тогда: ![]()
Учитывая ослабление вала шпоночной канавкой, следует увеличить его диаметр на 10%:
![]()
Округляем полученный диаметр вала согласно ГОСТ 6636-69.
Диаметр вала ![]()
Проверяем возможность применения насадной шестерни:
Шестерня делается насадной при условии ![]() . У нас
. У нас ![]() ,
, ![]() , следовательно,
, следовательно, ![]() . Условие соблюдается, значит, шестерню можно сделать насадной.
. Условие соблюдается, значит, шестерню можно сделать насадной.
7. Расчетный диаметр вала под подшипником «В»:
![]()
![]()
![]()
Тогда:
![]()
![]()
Тогда:
![]()
![]() с учетом ослабления вала шпоночной канавкой
с учетом ослабления вала шпоночной канавкой
8. Расчетный диаметр вала под подшипником «А»:
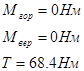
![]()
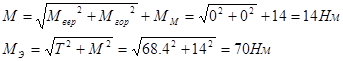
Тогда:
![]()
![]()
9. Диаметр вала под муфту:
Диаметр вала под муфту ![]()
Тогда имеем следующие диаметры вала:
Посадочный диаметр под муфту ![]()
Диаметр под подшипником, «А»: ![]()
Диаметр под подшипником, «В»: ![]()
Диаметр вала под шестерней ![]()
Проектный расчет тихоходного вала редуктора
Назначаем длины участков тихоходного вала:
![]()
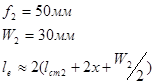
Длина ступичной части вала при ширине вала ![]()
![]() Принимаем
Принимаем ![]() .
.
Тогда ![]() .
.
Реакции опор в горизонтальной плоскости
![]()
![]()
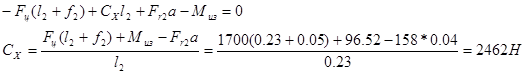
![]()
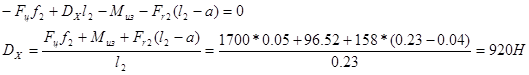
Проверка:
![]()
![]() , следовательно, реакции опор определены верно.
, следовательно, реакции опор определены верно.
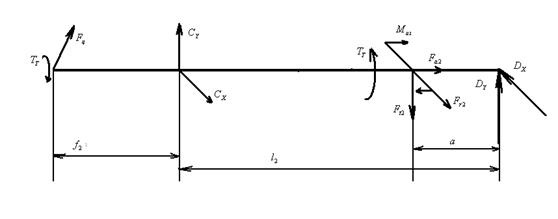
2. Реакции опор в вертикальной плоскости.
![]()
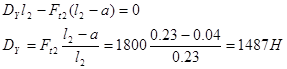
![]()
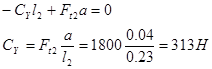
Проверка:
![]()
![]()
![]()
Следовательно, реакции опор в вертикальной плоскости определены верно.
3. Определим изгибающие моменты характерных сечений вала колеса:
- Под подшипником «С» в горизонтальной и вертикальной плоскости:
![]()
- под колесом в вертикальной и горизонтальной плоскости
![]()
![]()
- момент на шкиве цепной передачи:
![]()
Проверка в вертикальной плоскости:
![]()
Проверка в горизонтальной плоскости:
![]()
Следовательно, изгибающие моменты определены правильно.
4. Определим диаметры в характерных сечений вала:
Расчетный диаметр под подшипником «С»
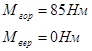
![]()
![]()
![]()
![]()
Принимаем ![]()
Такой же диаметр принимаем и под подшипником «D» ![]()
Определим расчетный диаметр вала под колесом:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Принимаем ![]()
Диаметр вала под шкивом цепной передачи:
![]()
![]()
![]()
Принимаем ![]()
Следовательно, имеем:
Диаметр вала под шкивом цепной передачи: ![]()
Диаметр вала под колесом ![]()
Диаметр вала вод подшипниками «С» и «D» ![]() ,
,![]()
Расчет валов на выносливость [4 c.274].
Быстроходный вал.
![]() [5. с.283]
[5. с.283]
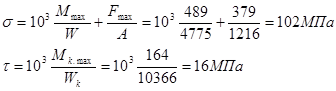
Где:
![]() - суммарный изгибающий момент
- суммарный изгибающий момент
![]() - крутящий момент
- крутящий момент![]()
![]() - осевая сила
- осевая сила
![]() - площадь сечения вала с пазом для призматической шпонки
- площадь сечения вала с пазом для призматической шпонки
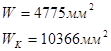 - моменты сопротивления сечения вала при расчете на изгиб и кручение. Сечение с пазом для призматической шпонки.
- моменты сопротивления сечения вала при расчете на изгиб и кручение. Сечение с пазом для призматической шпонки.
![]()
![]() Тогда:
Тогда:
![]()
![]()
Для опасных сечений вала определяем коэффициент запаса сопротивления усталости при совместном действии кручения и изгиба:
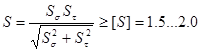 ,
,
где ![]() - коэффициент запаса сопротивления усталости по нормальным напряжениям.
- коэффициент запаса сопротивления усталости по нормальным напряжениям.
![]() > 2 –
> 2 –
следовательно, пластическая деформация будет отсутствовать.
Тихоходный вал.
![]()
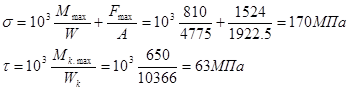
Где:
![]() - суммарный изгибающий момент
- суммарный изгибающий момент
![]() - крутящий момент
- крутящий момент![]()
![]() - осевая сила
- осевая сила
![]() - площадь сечения вала с пазом для призматической шпонки
- площадь сечения вала с пазом для призматической шпонки
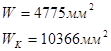 - моменты сопротивления сечения вала при расчете на изгиб и кручение. Сечение с пазом для призматической шпонки.
- моменты сопротивления сечения вала при расчете на изгиб и кручение. Сечение с пазом для призматической шпонки.
![]()
![]() Тогда:
Тогда:
![]()
![]()
Для опасных сечений вала определяем коэффициент запаса сопротивления усталости при совместном действии кручения и изгиба:
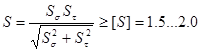 ,
,
где ![]() - коэффициент запаса сопротивления усталости по нормальным напряжениям.
- коэффициент запаса сопротивления усталости по нормальным напряжениям.
![]() > 2 – следовательно, пластическая деформация будет отсутствовать.
> 2 – следовательно, пластическая деформация будет отсутствовать.
Расчет подшипников
Исходные данные:
Сила от муфты ![]()
Быстроходный вал.
Радиальные нагрузки на подшипники ![]()
Внешняя осевая нагрузка ![]()
Частота вращения быстроходного вала ![]()
Посадочный диаметр на муфту ![]()
Диаметр под подшипником, «А»: ![]()
Диаметр под подшипником, «В»: ![]()
Диаметр вала под шестерней ![]()
Расстояние между подшипниками ![]()
Требуемый ресурс подшипников ![]()
Режим работы – спокойная равномерная нагрузка
Температура подшипникового узла ![]()
График нагрузки:
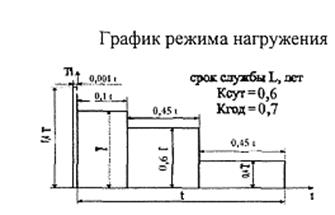
Быстроходный вал
В горизонтальной плоскости:
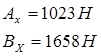
В вертикальной плоскости:
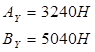
Значение реакции от силы ![]() прибавляется к результирующей реакции в опоре «А»:
прибавляется к результирующей реакции в опоре «А»:
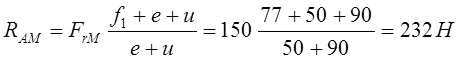
В опоре «В» от муфты:
![]()
Радиальная нагрузка от муфты в опоре «А»:
![]()
Радиальная нагрузка от муфты в опоре «В»:
![]()
1. 1. Назначаем роликовые радиально-упорные подшипники с коническими роликами (наиболее распространенный вид подшипников для конических передач), ГОСТ 333-79, так как на них действуют радиальные и осевые нагрузки.
Для подшипника «А» ![]() :
:
![]()
Следовательно, [2 c.266] назначаем подшипник «А» - роликоподшипник, с установкой в растяжку.
Аналогично для подшипника «В»: ![]()
Назначаем подшипник «В» - роликоподшипник, с установкой в растяжку.
2. Назначаем типоразмер подшипников.
Подшипник «А»:
![]()
![]()
Подшипник «В»
![]()
![]()
Исходя из этого, назначаем подшипники тяжелой серии диаметров: типоразмер 1027309A
[4. с.505], имеющий ![]() ,
, ![]() , коэффициент осевой нагрузки
, коэффициент осевой нагрузки ![]() ,
, ![]() , динамическую грузоподъемность
, динамическую грузоподъемность ![]() , статическую грузоподъемность
, статическую грузоподъемность ![]() ,
,![]()
3. Определяем осевые составляющие нагрузок.
Для подшипника «В»
![]()
Для подшипника «А»
![]()
Следовательно [2. c267]:
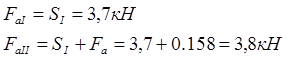
4. Определяем эквивалентную динамическую нагрузку
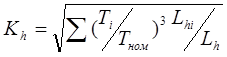
Где:
![]() - продолжительность работы подшипника при действии нагрузки от
- продолжительность работы подшипника при действии нагрузки от ![]() .
.
![]() - требуемый срок службы подшипника.
- требуемый срок службы подшипника. ![]()
Так как в редукторах не производится смена подшипников, то срок службы подшипника равен сроку службы редуктора ![]() .
.
Тогда 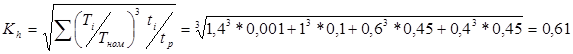
При постоянной нагрузке ![]() ,
, ![]() , где
, где
![]()
Где: ![]() - кинематический коэффициент, учитывающий снижение долговечности при неподвижном внутреннем кольце подшипника.
- кинематический коэффициент, учитывающий снижение долговечности при неподвижном внутреннем кольце подшипника.
У нас ![]() - при подвижном внутреннем кольце подшипника.
- при подвижном внутреннем кольце подшипника.
При равномерной нагрузке коэффициент безопасности ![]() .
.
Температурный коэффициент ![]() , при
, при ![]() .
.
![]() - радиальная и осевая нагрузки, действующие на подшипник при номинальной нагрузке
- радиальная и осевая нагрузки, действующие на подшипник при номинальной нагрузке ![]() .
.
![]() - коэффициенты радиальной и осевой нагрузок, назначаемые для конических роликоподшипников по ГОСТ 18855-82 в зависимости от отношения
- коэффициенты радиальной и осевой нагрузок, назначаемые для конических роликоподшипников по ГОСТ 18855-82 в зависимости от отношения ![]() .
.
Для подшипника «В»:
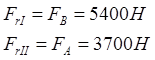
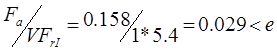
Следовательно, ![]()
Для подшипника «А»
![]()
Следовательно, ![]()
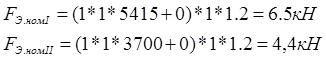
Так как подшипник «В» более нагружен, то все дальнейшие расчеты ведем для него.
![]()
5. Расчетная долговечность назначенного подшипника 1027309A в опоре «В»:
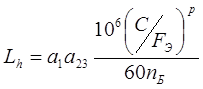
![]() при вероятности безотказной работы
при вероятности безотказной работы ![]()
Для роликовых подшипников ![]()
Для роликовых подшипников при обычных условиях эксплуатации ![]()
Тогда:
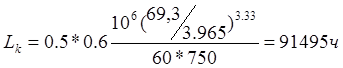 >
>![]() , что удовлетворяет требованиям.
, что удовлетворяет требованиям.
Следовательно для быстроходного вала оставим два подшипника 1027309А тяжелой серии.
Тихоходный вал
1. Назначаем роликовые радиально-упорные подшипники с коническими роликами (наиболее распространенный вид подшипников для конических передач), ГОСТ 333-79, так как на них действуют радиальные и осевые нагрузки.
Для подшипника «С» ![]() :
:
![]()
Следовательно, [2 c.266] назначаем подшипник «С» - роликоподшипник, с установкой враспор.
Аналогично для подшипника «D»: ![]()
Назначаем подшипник «В» - роликоподшипник, с установкой враспор.
2. Назначаем типоразмер подшипников.
Подшипник «C»:
![]()
![]()
Подшипник «D»
![]()
![]()
Исходя из этого, назначаем подшипники легкой серии диаметров: типоразмер 72310А
[4. с.504], имеющий ![]() ,
, ![]() , коэффициент осевой нагрузки
, коэффициент осевой нагрузки ![]() ,
, ![]() , динамическую грузоподъемность
, динамическую грузоподъемность ![]() , статическую грузоподъемность
, статическую грузоподъемность ![]()
3. Определяем осевые составляющие нагрузок.
Для подшипника «D»
![]()
Для подшипника «С»
![]()
![]()
Следовательно [2. c267]:
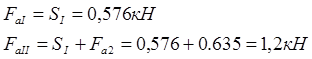
4. Определяем эквивалентную динамическую нагрузку
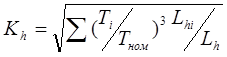
Где:
![]() - продолжительность работы подшипника при действии нагрузки от
- продолжительность работы подшипника при действии нагрузки от ![]() .
.
![]() - требуемый срок службы подшипника.
- требуемый срок службы подшипника. ![]()
Так как в редукторах не производится смена подшипников, то срок службы подшипника равен сроку службы редуктора ![]() .
.
Тогда
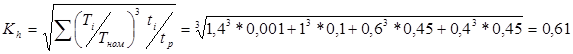
При постоянной нагрузке ![]() ,
, ![]() , где
, где
![]()
Где: ![]() - кинематический коэффициент, учитывающий снижение долговечности при неподвижном внутреннем кольце подшипника.
- кинематический коэффициент, учитывающий снижение долговечности при неподвижном внутреннем кольце подшипника.
У нас ![]() - при подвижном внутреннем кольце подшипника.
- при подвижном внутреннем кольце подшипника.
При наличии цепной передачи, нагрузка не будет равномерной, следовательно![]() .
.
Температурный коэффициент ![]() , при
, при ![]() .
.
![]() - радиальная и осевая нагрузки, действующие на подшипник при номинальной нагрузке
- радиальная и осевая нагрузки, действующие на подшипник при номинальной нагрузке ![]() .
.
![]() - коэффициенты радиальной и осевой нагрузок, назначаемые для конических роликоподшипников по ГОСТ 18855-82 в зависимости от отношения
- коэффициенты радиальной и осевой нагрузок, назначаемые для конических роликоподшипников по ГОСТ 18855-82 в зависимости от отношения ![]() .
.
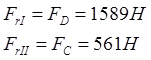
Для подшипника «D»:
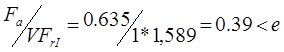
Следовательно, 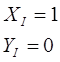
Для подшипника «А»
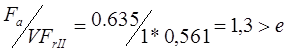
Следовательно, 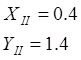
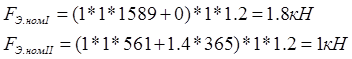
Так как подшипник «D» более нагружен, то все дальнейшие расчеты ведем для него.
![]()
5. Расчетная долговечность назначенного подшипника 1027308А в опоре «В»:
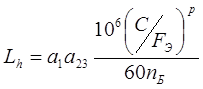
![]() при вероятности безотказной работы
при вероятности безотказной работы ![]()
Для роликовых подшипников при обычных условиях эксплуатации ![]()
Тогда:
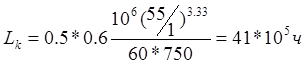 >
>![]() , что удовлетворяет требованиям.
, что удовлетворяет требованиям.
Следовательно, для тихоходного вала оставим два подшипника 7210А легкой серии.
Похожие работы
-
Кинематический и силовой расчет привода 2
1 Кинематический и силовой расчет привода 1.1 Выбор электродвигателя Определим потребляемую мощность привода по формуле: /1000, – тяговая сила конвейера, Н;
-
Кинематический расчет привода ленточного конвейера и расчет червячной передачи
Кинематическая схема привода ленточного конвейера. Кинематический расчет электродвигателя. Определение требуемуй мощности электродвигателя, результатов кинематических расчетов на валах, угловой скорости вала двигателя. Расчет зубчатых колес редуктора.
-
Проектирование привода ленточного конвейера
Проведение выбора электродвигателя, материалов шестерен и колес, смазки, муфт, определение допускаемых напряжений. Расчет тихоходной и быстроходной ступеней редуктора, ведомого и ведущего валов, подшипников. Проверка прочности шпоночных соединений.
-
Конструирование электропривода 2
Схема привода Привод состоит : 1- Электродвигатель 2- Ременная передача 3- Редуктор конический одноступенчатый 4- Муфта 5- Барабан конвейера Исходные данные:
-
Особенности проектирования трехступенчатого цилиндрического редуктора
Методика проектирования трехступенчатого цилиндрического редуктора. Порядок определения допускаемых напряжений. Особенности расчета 3-х ступеней редуктора, промежуточных валов и подшипников для них. Специфика проверки прочности шпоночных соединений.
-
Расчет зубчатой передачи
Содержание Введение……………..…………………………………..……………..2 Анализ кинематической схемы…………..……..………………..2 Кинематический расчет привода…………………………………3
-
Структура и принцип работы механизма
Определение передаточного отношения и разбиение его по ступеням, окружных и угловых скоростей зубчатых колес и крутящих моментов на валах с учетом КПД. Материал и термообработка зубчатых колес. Кинематический и геометрический расчет зубчатой передачи.
-
Проектирование привода силовой установки
Кинематические расчеты, выбор электродвигателя, расчет передаточного отношения и разбивка его по ступеням. Назначение материалов и термообработки, расчет допускаемых контактных напряжений зубчатых колес, допускаемых напряжений изгиба, размеров редуктора.
-
Проектирование конического редуктора
Произведение расчета мощности электродвигателя, кинематических параметров вала (частота вращения, угловая скорость), определение конусного расстояния, ширины венца, модуля передачи, внешнего диаметра колес с целью проектирования конического редуктора.
-
Расчет мощности двигателя
Выбор электродвигателя, кинематический расчет и схема привода. Частоты вращения и угловые скорости валов редуктора и приводного барабана. Расчет зубчатых колес редуктора. Выносливость зубьев по напряжениям изгиба. Расчёт вращающих моментов вала.