Система автоматического регулирования температуры газов в газотурбинном двигателе

Система автоматического регулирования температуры газов в газотурбинном двигателе .

Структурная схема:

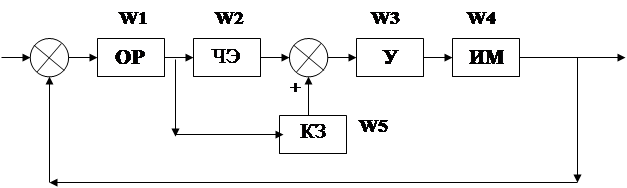
где:

ОР – объект регулирования;

ЧЭ – чувствительный элемент;

У – усилитель;

ИМ – исполнительный механизм;

КЗ – корректирующее звено;

Значения заданных параметров для исследуемой системы

Описание работы реальной системы:

В данной работе рассматривается система автоматического регулирования температуры газов в газотурбинном двигателе самолета. КЗ, которое в данном случае является реальным дифференцирующим звеном, реагирует на поступающий сигнал от ОР и дифференцируя его во времени, прогнозирует изменение температуры, т.е., система реагирует на малейшее отклонение температуры от заданной, не допуская критического ее понижения. Затем сигнал из сумматора поступает на усилитель, а с него на исполнительный механизм, который выполняет

требуемую коррекцию температуры.
ХОД РАБОТЫ

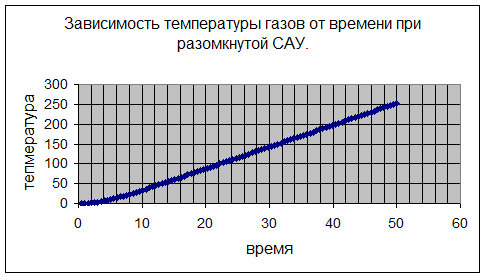
1) САУ разомкнута.

Структурная схема:

На графике видно, что система неустойчива.

При аналитической проверке система будет являться устойчивой, если все корни его характеристического уравнения лежат в левой полуплоскости. Проверяется это при помощи критерия устойчивости Гурвица. Согласно ему, для того, чтобы корни характеристического уравнения лежали строго в левой полуплоскости, необходимо и достаточно, чтобы главный определитель матрицы Гурвица и все его диагональные миноры были больше нуля.

Передаточная функция:

где 3,3S³ +4,1S² +S – характеристическое уравнение,

в котором а₀ =3,3, а₁ =4,1, а₂ =1, а₃ =0.

Поскольку свободный член характеристического уравнения равен нулю, значит один из корней равен нулю, и отсюда следует, что система находится на грани устойчивости.

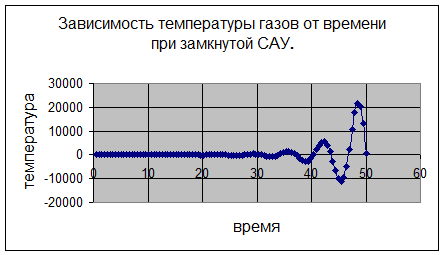
2)САУ замкнута.

Структурная схема:

На графике зависимости видно, что система не устойчива.

Передаточная функция:

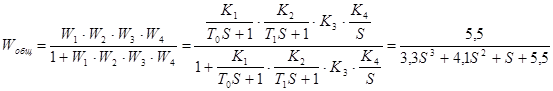
где 3,3S³ +4,1S² +S+5,5– характеристическое уравнение,

в котором а₁ =3,3, а₂ =4,1, а₃ =1, а₄ =5,5

Исследуем устойчивость системы с помощью критерия устойчивости Гурвица:

D₁ =а₁ =3,3>0,

D₂ =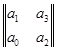=а_1· а₂ -а_0· а₃ =4,1-18,15=-14,05<0

Следовательно, замкнутая система не устойчива.

2)САУ с корректирующим звеном.

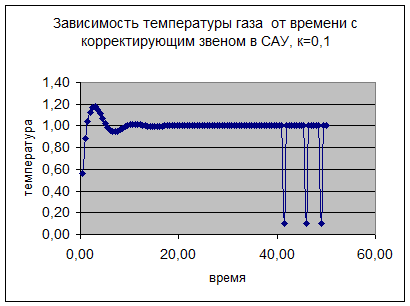
На этом этапе лабораторной работы рассматривается данная система, но уже с корректирующим звеном, для которого мы экспериментальным путём подбираем коэффициент коррекции, при котором система была бы устойчивой. Рассматривается два варианта, при k=0,1 и k=2.

а) Структурная схема:

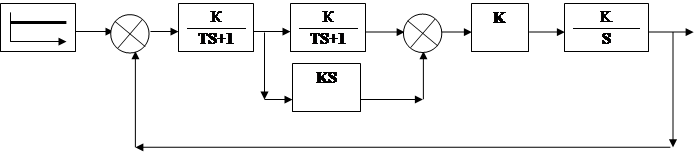
График зависимости показывает, что система не устойчива.

Передаточная функция:

где – характеристическое уравнение,

в котором а₀ =3, а₁ =4, а₂ =1, а₃ =5,5

Исследуем устойчивость системы с помощью критерия устойчивости Гурвица:

D₁ =а₁ =3>0,

D₂ =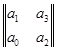=а₁ ·а₂ -а₀ ·а₃ =4,1·1-5,5·3,3=4,1-18,15<0

Отсюда можно сделать вывод, что при значении коэффициента k=0,1 система не устойчива.

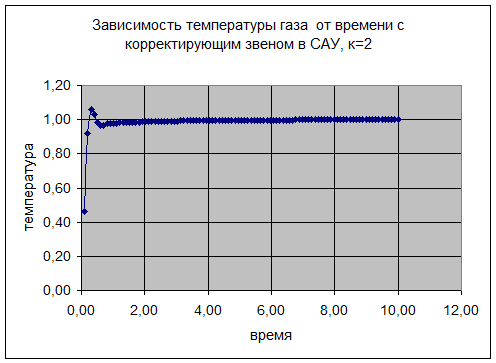
2)

График зависимости показывает, что система не устойчива.

Передаточная функция:

где – характеристическое уравнение,

в котором а₀ =1,8, а₁ =3,9, а₂ =1, а₃ =5,5

Исследуем устойчивость системы с помощью критерия устойчивости Гурвица:

D₁ =а₁ =1,8>0,

D₂ =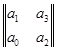=а₁ ·а₂ -а₀ ·а₃ =3,9·5,5-1·1,8=19,65<0

Отсюда можно сделать вывод, что при значении коэффициента К=2 система устойчива.

Вывод:

В данной лабораторной работе рассматривалась САУ регулирования температуры газов, поверялась ее устойчивость в зависимости от структуры.

В первом случае моделировалась разомкнутая САУ. Результаты исследования показали, что она находится на границе устойчивости (температура газа в газотурбинном двигателе непрерывно росла с течением времени), что указывает на ненадежность системы, так как она может в любой момент перейти в неустойчивое состояние.

Для повышения надежности системы вводится обратная отрицательная связь. Однако система оставалась неустойчивой, т.е. температура газа колебалась.

На следующем этапе в систему было включено корректирующее звено, и экспериментальным методом подбирался коэффициент, при котором система была бы устойчивой, и время регулирования было бы минимальным. Исходя из показаний графиков, и критерия Гаусса оптимальным коэффициентом КЗ является k=2.

Что касается самой среды моделирования, т.е. СИАМ, я могу сказать что она не смотря на неудобный интерфейс позволяет производить довольно сложные расчеты, если судить по документации, и позволяет увидеть результат моделирования конкретной системы в виде графика. Также ее плюсом является простота в эксплуатации и небольшие требования к вычислительной машине.