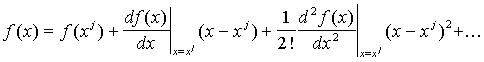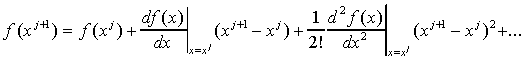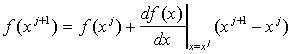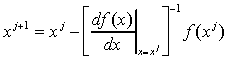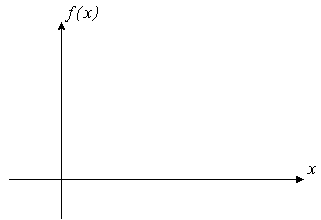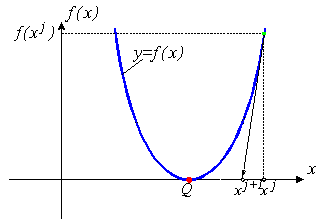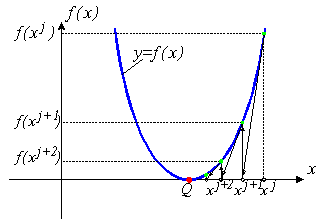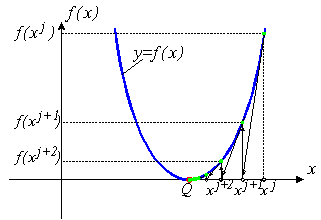Referat.me
/ / Метод решения уравнений Ньютона - Рафсона

Название: Метод решения уравнений Ньютона - Рафсона

Вид работы: доклад

Рубрика: Промышленность и производство

Размер файла: 37.15 Kb

Скачать файл: referat.me-304780.docx

Краткое описание работы: Метод Ньютона-Рафсона, также известный как Метод Ньютона, представляет собой обобщенный метод поиска корня уравнения Примем x = x в качестве j-го приближения к корню уравнения (1). Предположим, что x

Метод решения уравнений Ньютона - Рафсона

Метод Ньютона-Рафсона, также известный как Метод Ньютона, представляет собой обобщенный метод поиска корня уравнения

(1)

Примем x = xj в качестве j-го приближения к корню уравнения (1). Предположим, что xj не является решением. Следовательно, . Предположим также, что мы получили разложение в ряд Тейлора для уравнения (1) относительно точки x = xj :

(2)

Если примем в качестве следующего члена x = xj+1 , то уравнение (2) будет иметь вид:

(3)

Теперь предположим, что справедливо необязательное допущение того, что предыдущее приближение xj было удовлетворительным, так что xj+1 - xj мало. Если это предположение верно, мы можем пренебречь членами более высокого порядка в уравнении (3), так как n-я степень малой величины значительно меньше, чем малая величина для n>=2. В этом случае уравнение (3) может быть аппроксимировано следующим образом:

(4)

Нашей целью является выбор такого xj+1 , чтобы оно стало решением уравнения (1). Следовательно, если наше предыдущее предположение справедливо, xj+1 должно быть выбрано таким, что. Приравняв уравнение (4) к нулю и решив относительно xj+1 , получим:

(5)

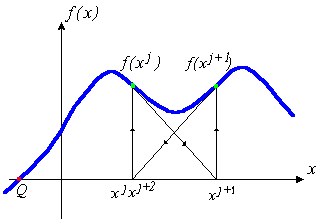
Уравнение (5) называется уравнением Ньютона - Рафсона. Если наше предположение, приведшее к выводу уравнения (5), справедливо, этот алгоритм будет сходящимся, но только в том случае, если точка начального приближения достаточно близка к точке решения. Геометрическая интерпретация сходящегося метода Ньютона - Рафсона приведена на рис. 1а.

а) метод сходится

б) метод не сходится

Рис.1. Геометрическая интерпретация метода Ньютона - Рафсона

Однако, если точка начального приближения далека от точки решения, то метод Ньютона - Рафсона может не сходиться совсем. Геометрическая интерпретация не сходящегося метода Ньютона - Рафсона приведена на рис. 1б.

Алгоритм

Назначение: поиск решения уравнения (1)

Вход:

Начальное приближение x0

Точность (число итераций I)

Выход:

xI - решение уравнения (1)

Инициализация:

calculate f’(x0 )

Шаги:

1. repeat:

2. calculate xi using (5)

3. let i=i+1

4. if i>I then break the cycle

end of repeat

Модификация алгоритма Ньютона для решения системы нескольких уравнений заключается в линеаризации соответствующих функций многих переменных, т. е. аппроксимации их линейной зависимостью с помощью частных производных. Например, для нулевой итерации в случае системы двух уравнений:

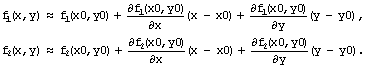
Чтобы отыскать точку, соответствующую каждой новой итерации, требуется приравнять оба равенства нулю, т.е. решить на каждом шаге полученную систему линейных уравнений.

Похожие работы