Название: Анализ шарнирного четырехзвенника и проектирование червячного редуктора
Вид работы: курсовая работа
Рубрика: Промышленность и производство
Размер файла: 527.13 Kb
Скачать файл: referat.me-305277.pdf
Краткое описание работы: Ìèíèñòåðñòâî îáðàçîâàíèÿ è êóëüòóðû Êûðãûçñêîé Ðåñïóáëèêè
Анализ шарнирного четырехзвенника и проектирование червячного редуктора
Ìèíèñòåðñòâî îáðàçîâàíèÿ è êóëüòóðû Êûðãûçñêîé Ðåñïóáëèêè
Êûðãûçñêèé Íàöèîíàëüíûé Óíèâåðñèòåò èì. Æ.Áàëàñàãûíà Ôàêóëüòåò õèìèè è õèìè÷åñêîé òåõíîëîãèè
Êàôåäðà íåîðãàíè÷åñêîé õèìèè è õèìè÷åñêîé òåõíîëîãèè
Ïîÿñíèòåëüíàÿ çàïèñêà ê êóðñîâîìó ïðîåêòó
ïî ïðèêëàäíîé ìåõàíèêå
Äèñöèïëèíà ïðèêëàäíàÿ ìåõàíèêà
Ñòóäåíò ___________________Äæåíëîäà Ð.Õ.
Ãðóïïà ÕÒ-01
Íàïðàâëåíèå (ñïåöèàëüíîñòü) Ò-08
Ðóêîâîäèòåëü ___________________Öîé Ó.À.
Äàòà çàùèòû __________________________
Îöåíêà __________________________
Áèøêåê-2004
Èñõîäíûå äàííûå: lAB , ì=0,05 l, ì=0,14 BC lDC , ì=0,16 lAD , ì=0,10
|
|||||||||
| ÊÍÓ.ÕÒ.000 ÏÇ | |||||||||
| Çàäàíèå | Ëèò. | Ìàññà | Ìàñøòàá | ||||||
| Èçì. | Ëèñò | ¹ äîêóì. | Ïîäïèñü | Äàòà | |||||
| Ðàçðàá. | Äæåíëîäà Ð.Õ. | ||||||||
| Ïðîâ. | Öîé Ó.À. | ||||||||
| Ò. êîíòð. | Ëèñò 2 | Ëèñòîâ 37 | |||||||
| ÊÍÓ ãðóïïà ÕÒ – 01 | |||||||||
| Í. Êîíòð. | |||||||||
| Óòâ. | |||||||||
1, ÑÒÐÓÊÒÓÐÍÛÉ ÀÍÀËÈÇ ÊÐÈÂÎØÈÏÍÎ-ÏÎËÇÓÍÍÎÃÎ ÌÅÕÀÍÈÇÌÀ
0 0 Íàçíà÷åíèå äàííîãî ìåõàíèçìà – ýòî ïðåîáðàçîâàíèå âðàùàòåëüíîãî äâèæåíèÿ çâåíà 1, â âîçâðàòíî- ïîñòóïàòåëüíîå äâèæåíèå çâåíà 3. Çâåíî 1, îáðàçóþùåå ñî ñòîéêîé 4 âðàùàòåëüíóþ êèíåìàòè÷åñêóþ ïàðó, íàçûâàþò êðèâîøèïîì; çâåíî 3, îáðàçóþùàÿ ñî ñòîéêîé 0 ïîñòóïàòåëüíóþ êèíåìàòè÷åñêóþ ïàðó, -ïîëçóíîì. Òàêîé ìåõàíèçì íàçûâàåòñÿ êðèâîøèïíî-ïîëçóííûì. Ðàññìàòðèâàåìûé ìåõàíèçì ñîñòîèò èç òðåõ ïîäâèæíûõ çâåíüåâ (n=3), è ñîäåðæèò ÷åòûðå îäíîïîäâèæíûå êèíåìàòè÷åñêèå ïàðû ïÿòîãî êëàññà (ð5 =4), èç êîòîðûõ îäíà ÿâëÿåòñÿ ïîñòóïàòåëüíîé (Ï30 ) - ñîåäèíÿåò ïîëçóí ñî ñòîéêîé 0, è òðè âðàùàòåëüíûìè (Â01 ,Â12 ,Â23 ) -ñîåäèíÿåò ñîîòâåòñòâåííî, ñòîéêó 0 ñ êðèâîøèïîì 1, êðèâîøèï 1 ñ øàòóíîì 2 è øàòóí 2 ñ ïîëçóíîì 3. Êèíåìàòè÷åñêèõ ïàð ÷åòâåðòîãî êëàññà â ìåõàíèçìå íåò, ò.å. ð4 =0. Ñòåïåíü ïîäâèæíîñòè ìåõàíèçìà îïðåäåëÿåòñÿ ïî ôîðìóëå ×åáûøåâà: W = 3n −2p 5 − p 4 = 3⋅3− 2⋅4−0 =1. Ìåõàíèçì ñîñòîèò èç îäíîé ãðóïïû Àññóðà, ñîäåðæàùåé øàòóí 2, ïîëçóí 3 è òðè êèíåìàòè÷åñêèå ïàðû (ðèñ.1), è íà÷àëüíîãî ìåõàíèçìà, ñîäåðæàùåãî êðèâîøèï 1, ñòîéêó 0 è îäíó êèíåìàòè÷åñêóþ ïàðó (ðèñ.2). Çâåíüÿ 2 è 3, ñ òðåìÿ êèíåìàòè÷åñêèìè ïàðàìè ïðåäñòàâëÿþò ñîáîé ãðóïïó Àññóðà II êëàññà âòîðîãî ïîðÿäêà âòîðîé ìîäèôèêàöèè. Êðèâîøèï 1 è ñòîéêà 6, ïðåäñòâëÿþò ñîáîé íà÷àëüíûé ìåõàíèçì. Ñòåïåíü ïîäâèæíîñòè ãðóïïû Àññóðà: Wçâ.2,3 = 3n⋅2p5 = 3⋅2 −2⋅3 = 0
À 3 0 Ðèñ.1 Ãðóïïà Àññóðà Ðèñ.2 Íà÷àëüíûé ìåõàíèçì Ôîðìóëà ñòðîåíèÿ ìåõàíèçìà: Â01 → [Â12 → Â23 → Ï30 ] Èç ñòðóêòóðíîãî àíàëèçà ìåõàíèçìà ñëåäóåò, ÷òî äëÿ ïîëó÷åíèÿ âïîëíå îïðåäåëåííûõ äâèæåíèé çâåíüåâ, äîñòàòî÷íî ïåðâîíà÷àëüíî çàäàòü îíîìó èç çâåíüåâ îïðåäåëåííîå äâèæåíèå. Ýòî è ïîäòâåðæäàåòñÿ ïðèíöèïîì îáðàçîâàíèÿ ìåõàíèçìîâ ïî Àññóðó. Ïî ôîðìóëå ñòðîåíèÿ ìåõàíèçìà ìîæíîïîñòðîèòü åãî ñòðóêòóðíóþ ñõåìó. |
||||||
| ÊÍÓ.ÕÒ.000 ÏÇ | Ëèñò | |||||
| 3 | ||||||
| Èçì. | Ëèñò | ¹ äîêóì. | Ïîäïèñü | Äàòà | ||
1.2 ÑÒÐÓÊÒÓÐÍÛÉ ÀÍÀËÈÇ ÌÅÕÀÍÈÇÌÀ ÏÎÄÀÒ×ÈÊÀ ÕËÅÁÎÐÅÇÀÒÅËÜÍÎÉ ÌÀØÈÍÛ ÌÐÕ-200 Ðàññìàòðèâàåìûé ìåõàíèçì ïîäàò÷èêà õëåáîðåçàòåëüíîé ìàøèíû ÌÐÕ – 200 ñîñòîèò èç ñëåäóþùèõ çâåíüåâ: íåïîäâèæíûõ äåòàëåé ìåõàíèçìà – ñòîåê 0; çâåíà 1 îáðàçóþùåãî ñî ñòîéêîé 0 âðàùàòåëüíî êèíåìàòè÷åñêóþ ïàðó - êðèâîøèïîì; êà÷àþùåãîñÿ çâåíà 3 - êîðîìûñëà; çâåíà 2 -øàòóíà. Ìåõàíèçì ïîäàò÷èêà õëåáîðåçàòåëüíîé ìàøèíû ÌÐÕ – 200, ñëóæèò äëÿ ïðåîáðàçîâàíèÿ âðàùàòåëüíîãî äâèæåíèÿ êðèâîøèïà 1 â âîçâðàòíî-âðàùàòåëüíîå äâèæåíèå çâåíà 3. Ò.ê. çâåíî 1 – êðèâîøèï (ñîâåðøàåò ïîëíûé îáîðîò), à çâåíî 3 – êîðîìûñëî (ñîâåðøàåò íåïîëíûé îáîðîò, òî ìåõàíèçì äàííîé ìàøèíû ÌÐÕ – 200, ÿâëÿåòñÿ êðèâîøèïíî-êîðîìûñëîâûì. Òðè ïîäâèæíûå çâåíà (n=3) è ñòîéêà 0 ìåõàíèçìà ïîäàò÷èêè õëåáîðåçàòåëüíîé ìàøèíû ÌÐÕ – 200 îáðàçóþò ÷åòûðå êèíåìàòè÷åñêèå ïàðû V êëàññà. Âðàùàòåëüíûå ïàðû (p5 =4) îáðàçîâàíû çâåíüÿìè 0 è 1, 1 è 2, 2 è 3, 3 è 0 (B01 , B12 , B23 , B30 ). Ñòåïåíü ïîäâèæíîñòè ìåõàíèçìà îïðåäåëÿåòñÿ ïî ôîðìóëå ×åáûøåâà: W =3n−2p5 −p4 =3⋅3−2⋅4−0 =1 ò.å. ìåõàíèçì èìååò îäíî âåäóùåå çâåíî. Ìåõàíèçì õëåáîðåçàòåëüíîé ìàøèíû ÌÐÕ – 200 ñîñòîèò èç îäíîé ãðóïïû Àññóðà, ñîäåðæàùåé øàòóí 2 è êîðîìûñëî 3, è èç íà÷àëüíîãî ìåõàíèçìà, âêëþ÷àþùåãî êðèâîøèï 1 è ñòîéêó 0 (ðèñ 1,2). Ãðóïïîé Àññóðà íàçûâàþò êèíåìàòè÷åñêóþ öåïü, ïîëó÷àþùàÿ íóëåâóþ ïîäâèæíîñòü ïîñëå ïðèñîåäèíåíèÿ åå ê ñòîéêå. Wãð2,3 =3n−2p5 =3⋅2−2⋅3=0 Çâåíî 2 è 3 ñ òðåìÿ êèíåìàòè÷åñêèìè ïàðàìè B, C, D îáðàçóþò ãðóïïó Àññóðà II êëàññà âòîðîãî ïîðÿäêà ïåðâîé ìîäèôèêàöèè. Êðèâîøèï 1 è ñòîéêà 0, ïðåäñòàâëÿþò ñîáîé íà÷àëüíûé ìåõàíèçì.
1 ðèñ.1. Ãðóïïà Àññóðà ðèñ.2. Íà÷àëüíûé ìåõàíèçì Ôîðìóëà ñòðîåíèÿ ìåõàíèçìà: B01 → [B12 →B23 →B30] |
||||||
| ÊÍÓ.ÕÒ.000 ÏÇ | Ëèñò | |||||
| 4 | ||||||
| Èçì. | Ëèñò | ¹ äîêóì. | Ïîäïèñü | Äàòà | ||
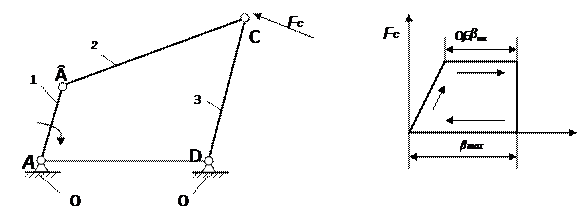
2.ÊÈÍÅÌÀÒÈ×ÅÑÊÈÉ ÀÍÀËÈÇ ÌÅÕÀÍÈÇÌÀ ÏÎÄÀÒ×ÈÊÀ ÕËÅÁÎÐÅÇÀÒÅËÜÍÎÉ ÌÀØÈÍÛ ÌÐÕ-200 2.1 Ïîñòðîåíèå ïëàíîâ ïîëîæåíèé ìåõàíèçìà ïîäàò÷èêà õëåáîðåçàòåëüíîé ìàøèíû ÌÐÕ-200 Ïðèíèìàþ ïðîèçâîëüíóþ äèíó êðèâîøèïà íà ÷åðòåæå AB=50 ìì. Ìàñøòàá äëèíû: l 0,05 µ
l
= AB
= AB 50 Ìàñøòàá äëèíû çâåíüåâ: l 0,14 BC = BC
= CD = CD
= µ l 0,001 l 0,1 AD = AD
= µ l 0,001 Ïî ïîëó÷åííûì äàííûì ñòðîèì ñõåìó ìåõàíèçìà â 12 ïîëîæåíèÿõ. Äëÿ ýòîãî ïðîâîäèì îêðóæíîñòü ðàäèóñîì À è äåëèì åå íà 12 ðàâíûõ ÷àñòåé, íà÷èíàÿñ íóëåâîãî.  êà÷åñòâå íóëåâîãî ïîëîæåíèÿ âûáèðàåì òî, ïðè êîòîðîì êîðîìûñëî îêàçûâàåòñÿ â ëåâîì êðàéíåì ïîëîæåíèè, äëÿ ÷åãî íà ðàññòîÿíèè AD íàìå÷àåì òî÷êó D è èç íåå êàê èç öåíòðà îïèøåì äóãó ðàäèóñîì CD. Èç òî÷êè À êàê èç öåíòðà ñäåëàåì íà ýòîé äóãå äâå çàñå÷êè – îäíó ðàäèóñîì CB-AB – ýòî áóäåò íóëåâîå ïîëîæåíèå òî÷êè Ñ, ò.å. Ñ0 , äðóãóþ – ðàäèóñîì CB+AB – ýòî áóäåò òî÷êà C8 , ñîîòâåòñòâóþùàÿ êðàéíåìó ïðàâîìó ïîëîæåíèþ êîðîìûñëà CD. Òî÷êè äåëåíèÿ îêðóæíîñòåé ðàäèóñà AB ñîåäèíÿåì ïðÿìûìè ëèíèÿìè ñ òî÷íîé A, îáîçíà÷àåì B0 , B1 ,…, B11 èç íèõ ðàäèóñîì BC ïðîâîäèì çàñå÷êè íà äóãå ðàäèóñà DC. Ïîëó÷åííûå òî÷êè C0 , C1 ,…, C11 ñîåäèíÿåì ïðÿìûìè ëèíèÿìè ñîîòâåòñòâåííî ñ òî÷êàìè B0 , B1 ,…, B11 è ñ òî÷êîé D. Òàêèì îáðàçîì, ÿ ïîëó÷èë 12 ïëàíîâ ìåõàíèçìà, ïîñòðîåííûõ â ìàñøòàáå µ l =0,001 ì/ìì. 2.2 Ïîñòðîåíèå ïëàíîâ ñêîðîñòåé òî÷åê çâåíüåâ ìåõàíèçìà ïîäàò÷èêà õëåáîðåçàòåëüíîé ìàøèíû ÌÐÕ-200 Îïðåäåëÿåì ñêîðîñòü òî÷êè Â: VB = ω1 •lAB =22•0,05 =1,1 ì/ñ. Äëÿ îïðåäåëåíèÿ ñêîðîñòè òî÷êè Ñ ñîñòàâëÿåì äâà âåêòîðíûõ óðàâíåíèÿ:
VC =VB +VCB, VC =VD +VCD . Ðåøàÿ ýòè óðàâíåíèÿ ãðàôè÷åñêè, ïîëó÷àåì ïëàíû ñêîðîñòåé. Ïîñòðîåíèå ïëàíà ñêîðîñòåé ïðîèçâîäèòüñÿ ñëåäóþùèì îáðàçîì: Èç ïðîèçâîëüíî âûáðàííîãî ïîëþñà ð îòêëàäûâàåì îòðåçîê ïðîèçâîëüíî âçÿòîé äëèíû ðb=44 ììâ íàïðàâëåíèè, ïåðïåíäèêóëÿðíîì çâåíó À â 1-îì ïîëîæåíèè, â ñòîðîíó íàïðàâëåíèÿ óãëîâîé ñêîðîñòè ω 1 . Ìàñøòàáíûé êîýôôèöèåíò ïëàíà ñêîðîñòåé áóäåò: V 1,1 µ
V
= B
=
VC = pc• µV =3•0,025 =0,075ì/ñ
VCD =cb• µV =41 •0,025 =1,025ì/ñ |
||||||
| ÊÍÓ.ÕÒ.000 ÏÇ | Ëèñò | |||||
| 5 | ||||||
| Èçì. | Ëèñò | ¹ äîêóì. | Ïîäïèñü | Äàòà | ||
Óãëîâàÿ ñêîðîñòü êîðîìûñëà îïðåäåëÿåòñÿ ïî ôîðìóëå: V 0,075 ω
CD
= CD
=
V 1,025 ω
CB
= CB
= lCB 0,14 Ðåçóëüòàòû âû÷èñëåíèé ñêîðîñòåé ñâåäåíû â òàáëèöó 1. 2.3 Ïîñòðîåíèå ãðàôèêà èçìåíåíèÿ ñèëû ïîëåçíîãî ñîïðîòèâëåíèÿ Ïî óñëîâèþ çàäàíèÿ ïëàí óñêîðåíèé è ñèëîâîé àíàëèçìåõàíèçìà ñëåäóåò âûïîëíèòü äëÿ ïîëîæåíèÿ ìåõàíèçìà, êîãäà òî÷êà Ñ ðàçâèâàåò ìàêñèìàëüíóþ ìîùíîñòü Nmax =FC ⋅VC . Äëÿ îïðåäåëåíèÿ Nmax íåîáõîäèìî çíàòü çíà÷åíèå ñèëû FC âî âñåõ ïîëîæåíèÿõ ìåõàíèçìà, ñ òåì ÷òî áû ïîòîì èç ïðîèçâåäåíèé FC ⋅VC âûáðàòü íàèáîëüøåå. Ïîýòîìó ñëåäóåò ïîñòðîèòü ãðàôèê FC = (β max ). Äëÿ ýòîãî ïðîâîæó ëèíèþ ÷åðåç äâà êðàéíèõ ïîëîæåíèÿ â òî÷êàõ Ñ0 è Ñ8 . Çàòåì ïðîâîæó ëèíèþ íàä Ñ0 Ñ8 ïàðàëëåëüíóþ åé – ïîëó÷àåì îñü àáñöèññ, (ñì. ñõåìó), ïðîâåäÿ ê íåé ïåðïåíäèêóëÿð èç òî÷êè Ñ0 , ïîëó÷àåì òî÷êó à – íà÷àëî êîîðäèíàò, à ïðîâåäÿ ïåðïåíäèêóëÿð èç òî÷êè Ñ8 , ïîëó÷àåì òî÷êó d, îãðàíè÷èâàþùóþ õîä òî÷êè Ñ. Èç òî÷êè à ïðîâîäèì îñü îðäèíàò. Èç òî÷êè d ïî îñè àáñöèññ îòëîæó îòðåçîê 0,6β max, âîññòàíàâëèâàåì èç ïîëó÷åííîé òî÷êè F0 îðäèíàòó F0 Fmax ïðîèçâîëüíîé äëèíû (â ìîåì ñëó÷àå F0 Fmax =36 ìì). Ýòà îðäèíàòà âûðàæàåòñÿ â ìàñøòàáå µF ìàêñèìàëüíóþ ñèëó ïîëåçíîãî ñîïðîòèâëåíèÿ FCmax . Âåëè÷èíó ìàñøòàáíîãî êîýôôèöèåíòà íàéäó èç âûðàæåíèÿ: F 1,8
ymax 36 Ñîåäèíèâ ïðÿìîé ëèíèåé òî÷êè a è Fm è ïðîâåäÿ èõ òî÷êè Fm ãîðèçîíòàëüíóþ ëèíèþ íà ðàññòîÿíèå 0,6β max îò îñè îðäèíàò, ïîëó÷àåì èñêîìûé ãðàôèê FC (β max ). Ïðè äâèæåíèè òî÷êè Ñ â ïðàâî ñèëà FC óâåëè÷èâàåòñÿ ïî ëèíåéíîìó çàêîíó äî ìàêñèìàëüíîãî çíà÷åíèÿ (òî÷êà Fm ), à ïðè äâèæåíèè âëåâî ñèëû FC ðàâíà íóëþ. Ïðîâåäÿ èç òî÷åê C1 ,C2 ,C3 ,C4 ,C5 ,C6 ,C7 ,C8 âåðòèêàëüíûå ëèíèè äî ïåðåñå÷åíèÿ èõ ñ ãðàôèêîì FC (β max ), ïîëó÷àåì ñîîòâåòñòâóþùèå êîîðäèíàòû y 1 , y 2 ,..., y 8 , ïî êîòîðûì ìîæíî ñóäèòü îâåëè÷èíå ñèëû ñîïðîòèâëåíèÿ â ëþáîì ïîëîæåíèè ìåõàíèçìà. Ðåçóëüòàòû âû÷èñëåíèé ñâåäåíû â òàáëèöó 1. Àíàëèç äàííûõ òàáëèöû 1 ïîêàçûâàåò, ÷òî íàèáîëüøóþ ìîùíîñòü ìåõàíèçì ïîäàò÷èêà õëåáîðåçàòåëüíîé ìàøèíû ðàçâèâàåò â ÷åòâåðòîì ïîëîæåíèè, ò.å. Nmax =1800⋅1,3=2,34êÂò, òàê êàê ìîùíîñòü Nîïðåäåëÿåòñÿ ïðîèçâåäåíèåì FC ⋅VC , à ýòè ïàðàìåòðû äàþò ìàêñèìàëüíîå ïðîèçâåäåíèå èìåííî â ïÿòîì ïîëîæåíèè. Ñëåäîâàòåëüíî, ïëàí óñêîðåíèé íåîáõîäèìî ñòðîèòü äëÿ ìåõàíèçìà ïîäàò÷èêà õëåáîðåçàòåëüíîé ìàøèíû, êîãäà îí íàõîäèòñÿ â ïÿòîì ïîëîæåíèè.  ýòîì æå ïîëîæåíèè ìåõàíèçìà îïðåäåëÿþòñÿ ðåàêöèè â êèíåìàòè÷åñêèõ ïàðàõ çâåíüåâ è óðàâíîâåøèâàþùàÿ ñèëà Fy . 2.4 Ïîñòðîåíèå ïëàíà óñêîðåíèé Èç àíàëèçà ïëàíîâ ñêîðîñòåé âèäíî, ÷òî íàèáîëüøåé ìîùíîñòüþ òî÷êà Ñ áóäåò îáëàäàòü â 5– îì ïîëîæåíèè, ò.ê. ïðè ïîñòîÿííîé ñèëå ìîùíîñòü çàâèñèò îò ñêîðîñòè, à ñêîðîñòü òî÷êè Ñ ìàêñèìàëüíà â 5 – îì ïîëîæåíèè. Ïîýòîìó ïëàí óñêîðåíèé ñòîèì äëÿ 5 - ãî ïîëîæåíèÿ. Îïðåäåëÿåì óñêîðåíèå òî÷êè Â:
Äëÿ îïðåäåëåíèÿ óñêîðåíèÿ òî÷êè Ñ ñîñòàâëÿåì äâà âåêòîðíûõ óðàâíåíèÿ: ~ ~ n l n laC =aB +aCB +aCB, aC =aD +aCD +aCD. |
||||||
| ÊÍÓ.ÕÒ.000 ÏÇ | Ëèñò | |||||
| 6 | ||||||
| Èçì. | Ëèñò | ¹ äîêóì. | Ïîäïèñü | Äàòà | ||
n n Íîðìàëüíûå óñêîðåíèÿ a è CB a îïðåäåëÿþòñÿ: CD n VCB 2 0,72 2 cCB
= = lCB 0,14 2 2 V cCDn = C
=1 Âûáèðàåì ïðîèçâîëüíî ïîëþñ Π è èç íåãî ïàðàëëåëüíî êðèâîøèïó ÀÂ â íàïðàâëåíèè îò À ê Â ïðîâîäèì ïðÿìóþ Ïb ïðîèçâîëüíîé äëèíû (ïðèìåì Ïb=96,8 ìì). Ìàñøòàá ïëàíà óñêîðåíèé áóäåò:
µa
Èç ïîëþñà Ï ïðîâîäèì ïðÿìóþ ïàðàëëåëüíî CD â íàïðàâëåíèè îò C ê D è íà íåé îòêëàäûâàåì îòðåçîê: aCD n 10,56 ∏Cn
= = µa 0,25 Èç òî÷êè b ïðîâîäèì ïðÿìóþ ïàðàëëåëüíî BC â íàïðàâëåíèè îò C ê B è íà íåé îòêëàäûâàåì îòðåçîê: aCB n 3,5 bbn
= = µa 0,25 Èç òî÷åê ñn è bn ïðîâîäèì ïðÿìûå ëèíèè ïåðïåíäèêóëÿðíî Ïñï è bbn äî ïåðåñå÷åíèÿ èõ â òî÷êå Ñ. Îòðåçêè ññï è bn c èçîáðàæàþò â ìàñøòàáå µ à òàíãåíöèàëüíûå óñêîðåíèÿ òî÷êè Ñ îòíîñèòåëüíî òî÷åê D è B. Îòðåçîê ñîåäèíÿþùèé ïîëþñ Ï ñ òî÷êîé Ñ, èçîáðàæàåò ïîëíîå óñêîðåíèå òî÷êè Ñìåõàíèçìà, à îòðåçêè, ñîåäèíÿþùèå ïîëþñ ñ ñåðåäèíàìè îòðåçêîâ Ïb, bc è Ïñ – ïîëíûå óñêîðåíèÿ öåíòðîâ ìàññ çâåíüåâ ìåõàíèçìà. Çíà÷åíèÿ óñêîðåíèé: ~ aCB l =bn c• µa =55•0,25 =13,75ìì/ñ2 ~ aCD l =cn c• µa =10•0,25 =5 ìì/ñ2 a =bc•µ =57 •0,25 =14,25 ìì/ñ2 CB a aCD =aC = Πc•µa =44•0,25 =11ìì/ñ2 aS 1 = ΠS1 • µa =48,4•0,25 =12,1 ìì/ñ2 aS 2 = ΠS2 • µa =69•0,25 =17,25ìì/ñ2 aS 3 = ΠS3 • µa =22•0,25 =5,5 ìì/ñ2 ~ l a 13,75 ε
CB
= CB
= lCB 0,14 ~ aCD
l 5 2 ε
CD
= = lCD 0,16 Òàíãåíöèàëüíûå óñêîðåíèÿ íàïðàâëåíû ïî ÷àñîâîé ñòðåëêå. |
||||||
| ÊÍÓ.ÕÒ.000 ÏÇ | Ëèñò | |||||
| 7 | ||||||
| Èçì. | Ëèñò | ¹ äîêóì. | Ïîäïèñü | Äàòà | ||
3.ÄÈÍÀÌÈ×ÅÑÊÈÉ ÀÍÀËÈÇ ÌÅÕÀÍÈÇÌÀ 3.1 Îïðåäåëåíèå èíåðöèîííûõ íàãðóçîê Ïðèíÿâ êîýôôèöèåíò (ïîãîííàÿ ìàññà) q=20 êã/ì, îïðåäåëÿåì ìàññû çâåíüåâ è èõ ñèëû âåñà: m1 =q•lAB =20•0,05 =1êã; G1 =m1 g=1 •9,8=9,8Í; m2 =q•lBC =20•014, =2,8êã; G2 =m2 g=2,8•9,8=27,44Í;m3 =q•lCD =20•016, =3,2êã; G3 =m3 g=3,2•9,8=31,36Í; Ñèëû èíåðöèè: FU 1 =m1 •aS 1 =1•12,1 =12,1 Í FU 2 =m2 •aS 2 =2,8•17,25 =48,3Í FU 3 =m3 •aS 13 =3,2•5,5 =17,6 Í Ìîìåíòû èíåðöèè çâåíüåâ:
I S2
I S3 Ìîìåíòû ñèë èíåðöèè: MU 2 =IS 2 •ξCB =0,0046•98,2 =0,45Í/ì MU 3 =IS 3 •ξCD =0,0068•31,2 =0,21Í/ì 3.2 Îïðåäåëåíèå ðåàêöèé â êèíåìàòè÷åñêèõ ïàðàõ Äëÿ îïðåäåëåíèÿ ðåàêöèé â êèíåìàòè÷åñêèõ ïàðàõ âîñïîëüçóþñü ïðèíöèïàìè Äàëàìáåðà è ñòàòè÷åñêîé îïðåäåëèìîñòüþ ãðóïïû Àññóðà. Âû÷åð÷èâàþ ãðóïïó Àñóðà (çâåíüÿ 2-3) â íàòóðàëüíóþ âåëè÷èíó (ìîæíî òàêæå èñïîëüçîâàòü óæå âû÷èñëåííûé ìàñøòàáíûé êîýôôèöèåíò µ l ) â ïîëîæåíèè 5 (ñì.ñõåìó) è ïðèêëàäûâàþ ê íåé â ñîîòâåòñòâóþùèõ òî÷êàõ âñå äåéñòâóþùèå ñèëû âåñà çâåíüåâ G2 , G3 ; ñèëû èíåðöèè â øàðíèðàõ  è D ðàñêëàäûâàþ íà íîðìàëüíûå è òàíãåíöèàëüíûå ñîñòàâëåíèÿ; ñèëó ïîëåçíîãî ñîïðîòèâëåíèÿ FC . Ñèëû èíåðöèè Fu2 è Fu3 íàïðàâëåíû ïðîòèâîïîëîæíî óñêîðåíèÿì as2 è as3 , à ìîìåíòû ñèë èíåðöèè Mu2 è Mu3 , íàïðàâëåíû ïðîòèâîïîëîæíî óãëîâûì óñêîðåíèÿì ξ CD è ξ CB . Îïðåäåëÿþ ðåàêöèè R è 12 τ R , äëÿ ÷åãî ñîñòàâèë óðàâíåíèÿ ðàâíîâåñèÿ êàæäîãî èç çâåíüåâ: 03 τ
Èç ýòèõ óðàâíåíèé ïîëó÷àåì: Fh -Gh +M R12τ = u2 1 2 2 u2
=48 BC 140 Gh -Fh +M R03τ = 3 4 u3 3 u3
=31 DC 160 Äëÿ îïðåäåëåíèÿ íîðìàëüíûõ ñîñòàâëÿþùèõ R è 12 τ R ñîñòàâëÿåì óðàâíåíèÿ ðàâíîâåñèÿ ãðóïïû Àññóðà: 03 τ
Äëÿ îïðåäåëåíèÿ ìàñøòàáà ñèë µ F ïðèìó, ÷òî íàèáîëüøàÿ ñèëà, âõîäÿùàÿ â ýòî óðàâíåíèå – FC èçîáðàæàåòñÿ îòðåçêîì fk äëèíîé â 60ìì. Òîãäà ìàñøòàá ïëàíà ñèë áóäåò: F 1800 µF
= C
= |
||||||
| ÊÍÓ.ÕÒ.000 ÏÇ | Ëèñò | |||||
| 8 | ||||||
| Èçì. | Ëèñò | ¹ äîêóì. | Ïîäïèñü | Äàòà | ||
Îñòàëüíûå ñèëû îïðåäåëÿþòñÿ íà ÷åðòåæå îòðåçêàìè:
ab= 12 ==0,56 ìì µF
bc= 2 ==0,91ìì µF
cd = u2 ==1,61 ìì µF G 31,36 de= 3
= µF 30 F 17,6 ef = u3
= µF 30 R 4,57 kl= 03
= µF 30 Äàííûå äëÿ ïîñòðîåíèÿ ïëàíà ñèë ãðóïïû Àññóðà ñâåäåíû â òàáëèöó 2. Ïðè ýòèì îòðåçêàì ñòðîèì ïëàí ñèë, íà÷èíàÿ ñ òî÷êè à; èç òî÷êè l ïðîâîæó ïðÿìóþ ïàðàëëåëüíóþ R03 n , à èç òî÷êè a – ïðÿìóþ, ïàðàëëåëüíóþ R Ýòè ïðÿìûå ïåðåñåêàþòñÿ â òî÷êå t (ñì. ïðèëîæåíèå). Îòðåçêè at è ltâ 12 n . ìàñøòàáå µF èçîáðàæàþò òàíãåíöèàëüíûå ñîñòàâëÿþùèå ðåàêöèé R è 12 n R , âåëè÷èíû êîòîðûõ îïðåäåëÿþòñÿ: 03 n R12 n =at⋅µ F =72⋅30 =2160H; R03 n =lt⋅µ F =38⋅30 =1140H. Äëÿ îïðåäåëåíèÿ âåëè÷èíû óðàâíîâåøèâàþùåé ñèëû Fó , äëÿ ÷åãî ñîñòàâëþ óðàâíåíèÿ ðàâíîâåñèÿ âåäóùåãî çâåíà: ∑M(A) =Fy ⋅AB−R12 ⋅h1 −G1 ⋅h2 =0, çâ.1 îòêóäà íàõîæó
F y 12 1 1 2 . Äëÿ îïðåäåëåíèÿ ðåàêöèé â øàðíèðå À (R01 ) çàïèøó óðàâíåíèå âåêòîðíîé ñóììû ñèë, äåéñòâóþùèõ íà êðèâîøèï:
∑F =Fy +R21 +G1 +Fu1 +R01 =0. çâ.1 Ïðè îïðåäåëåíèè ìàñøòàáà ïëàíà ñèë µF ÿ ïðèíÿë, ÷òî íàèáîëüøàÿ ñèëà âõîäÿùàÿ â óðàâíåíèå – Fy , èçîáðàæåííàÿ îòðåçêîì ab äëèíîé 108ìì. Èç ýòîãî îïðåäåëþ ìàñøòàá ïëàíà ñèë: Fy 2164,312
Äàííûå äëÿ ïîñòðîåíèÿ ïëàíà ñèë âåäóùåãî çâåíà ñâåäåíû â òàáëèöó 3; (ñì.ñõåìó). Èç ïëàíà ñèë âåäóùåãî çâåíà îïðåäåëèòüñÿ R01 : R01 =ea⋅µ F =1⋅20 =20Í. Òàêèì îáðàçîì, ìåòîäîì êèíåòîñòàòèêè îïðåäåëåíû ðåàêöèè âî âñåõ êèíåìàòè÷åñêèõ ïàðàõ è âåëè÷èíà óðàâíîâåøèâàþùåé ñèëû; óêàçàííûå çàäà÷è ðåøåíû äëÿ ìåõàíèçìà â 5-îì ïîëîæåíèè, êîãäà òî÷êà ïðèëîæåíèÿ ñèëû ïîëåçíîãî ñîïðîòèâëåíèÿ ðàçâèâàåò íàèáîëüøóþ ìîùíîñòü. |
||||||
| ÊÍÓ.ÕÒ.000 ÏÇ | Ëèñò | |||||
| 9 | ||||||
| Èçì. | Ëèñò | ¹ äîêóì. | Ïîäïèñü | Äàòà | ||
3.3 Ïîñòðîåíèå ãðàôèêà ïðèâåäåííûõ ìîìåíòîâ ñèë ñîïðîòèâëåíèÿ Ñèëà F îïðåäåëèòñÿ èç óðàâíåíèÿ ðàâíîâåñèÿ ðû÷àãà Æóêîâñêîãî: y Fy ⋅pb=Fc ⋅pc, îòêóäà F pc Fy
= pb
Ïðèíÿâ ìàêñèìàëüíóþ îðäèíàòó y max =53 ìì, îïðåäåëÿþ ìàñøòàá äèàãðàììû TC (ϕ): T 106,36 µ
T
= Cmax
= ymax 53 T Íàõîæó îðäèíàòû y= µ T Èíòåãðèðóÿ ãðàôè÷åñêè ýòó äèàãðàììó, ïîëó÷àþ äèàãðàììó ðàáîòû ñèë ñîïðîòèâëåíèÿ. ÎÊ =30ìì – ïðèíÿòîå ìíîþ ïîëþñíîå ðàññòîÿíèå. Ñîåäèíèâ ïðÿìîé ëèíèåé íà÷àëî è êîíåö ãðàôèêà AC (ϕ), ïîëó÷àþ ãðàôèê ðàáîò äâèæóùèõñÿ ñèë AD (ϕ). Äèôôåðåíöèðóÿ åãî, ïîëó÷àþ ãðàôèê ìîìåíòîâ äâèæóùèõñÿ ñèë – îí ïðåäñòàâëÿåò ñîáîé ïðÿìóþ ëèíèþ, ïàðàëëåëüíóþ àáñöèññå. Âåëè÷èíà ìîìåíòà äâèæóùèõ ñèë îïðåäåëÿåòñÿ: TD = yD •µT =21•2 =42Íì, ãäå óD - îðäèíàòà ãðàôèêà TD ( )ϕ. Ìîùíîñòü íà âàëó êðèâîøèïà îïðåäåëèòüñÿ ïî ôîðìóëå : P =TD ⋅ω 1 =42⋅22 =924Âò= 0,924ÊÂò. |
||||||
| ÊÍÓ.ÕÒ.000 ÏÇ | Ëèñò | |||||
| 10 | ||||||
| Èçì. | Ëèñò | ¹ äîêóì. | Ïîäïèñü | Äàòà | ||
Òàáëèöà 1
Òàáëèöà 2
Òàáëèöà 2
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ÊÍÓ.ÕÒ.000 ÏÇ | Ëèñò | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 11 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Èçì. | Ëèñò | ¹ äîêóì. | Ïîäïèñü | Äàòà | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Òàáëèöà 3
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ÊÍÓ.ÕÒ.000 ÏÇ | Ëèñò | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 12 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Èçì. | Ëèñò | ¹ äîêóì. | Ïîäïèñü | Äàòà | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
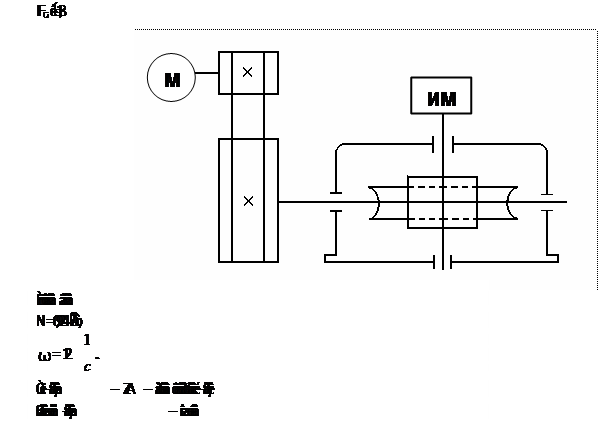
4.ÊÈÍÅÌÅÒÈ×ÅÑÊÈÉ ÐÀÑ×ÅÒ ÏÐÈÂÎÄÀ Èñõîäíûå äàííûå : N=0.924 êÂò ω =12ñ− 1 Ïîäáîð ýëåêòðîäâèãàòåëÿ: 4.1 ×àñòîòà âðàùåíèÿ âàëà èñïîëíèòåëüíîãî ìåõàíèçìà: n i =iðì ⋅içï = (2÷5) (⋅ 8÷40) = (16÷200);nîá =114,59⋅(16÷200) (= 1834÷22929); 4.2 Îáùèé êîýôôèöèåíò ïîëåçíîãî äåéñòâèÿ ïðèâîäà η = η çï ⋅η ïê 2 ⋅η ðï =0,85⋅0,992 ⋅0,95 =0,791; ηïê =0.99 – ê.ï.ä. ïàðû ïîäøèïíèêîâ êà÷åíèÿ; η÷ï =0.85 – ê.ï.ä. ÷åðâÿ÷íîé ïåðåäà÷è; ηïñ =0.95 – ê.ï.ä. ðåìåííîé ïåðåäà÷è. 4.3 Ïîòðåáíàÿ ìîùíîñòü ýëåêòðîäâèãàòåëÿ
4.4 Ïåðåäàòî÷íîå ÷èñëî ïðèâîäà
n3 114,59 4.5 Ïåðåäàòî÷íîå ÷èñëî ðåìåííîé ïåðåäà÷è i
içï 10 Z=4, òî U÷åðâ =10 Òàáëèöà 4.1
Îïðåäåëåíèå êèíåìàòè÷åñêèõ è ñèëîâûõ ïàðàìåòðîâ ïðèâîäà. 4.6 Ïåðåäàòî÷íûå ÷èñëà ñòóïåíåé ïåðåäà÷ ïðèâîäà Uðåì =2.513 U÷åðâ =10 Uîáù =Uðåì ⋅U÷åðâ =2,513⋅10 =25,13 4.7 ×àñòîòà âðàùåíèÿ âàëîâ ïðèâîäà: n1 =nýë.äâ =2880 n2 =n1 /Uðåì =2880/2,513=1145,9 n3 =n2 /U÷åðâ =1145,9/10=114,59 |
|||||||||||||||
| ÊÍÓ.ÕÒ.000 ÏÇ | Ëèñò | ||||||||||||||
| 13 | |||||||||||||||
| Èçì. | Ëèñò | ¹ äîêóì. | Ïîäïèñü | Äàòà | |||||||||||
Ìîùíîñòè. 4.8 Ìîùíîñòè íà âàëàõ: P3 =Pïð.â =0,924 êÂò P2 =P3 /η÷ï =0,924/0,85=1,087 êÂò P1 =P2 /ηðï =1,087/0,95=1,144 êÂò Âðàùàþùèå ìîìåíòû íà âàëàõ 4.9 Ìîìåíòû íà âàëàõ: P 1,144 T1
=9550 1
=9550 n1 2880 T2 =T1 ⋅Uðåì ⋅η ðåì =3,794⋅2,513⋅0,95 =7,689Íì T3 =T2 ⋅U÷åð ⋅η ÷åð =7,689⋅10⋅0,85 =65,356 Íì Òàáëèöà 4.2 Ðåçóëüòàòû êèíåìàòè÷åñêîãî ðàñ÷åòà
Òàáëèöà 4.3 Òåõíè÷åñêèå õàðàêòåðèñòèêè äâèãàòåëÿ
|
||||||||||||||||||||||||||||||||||||||||||||||||||
| ÊÍÓ.ÕÒ.000 ÏÇ | Ëèñò | |||||||||||||||||||||||||||||||||||||||||||||||||
| 14 | ||||||||||||||||||||||||||||||||||||||||||||||||||
| Èçì. | Ëèñò | ¹ äîêóì. | Ïîäïèñü | Äàòà | ||||||||||||||||||||||||||||||||||||||||||||||
5.ÐÀÑ×ÅÒ ×ÅÐÂß×ÍÎÉ ÏÅÐÅÄÀ×È 5.1 Èñõîäíûå äàííûå T2 =65,356 Íì - ìîìåíò íà âàëó ÷åðâÿ÷íîãî êîëåñà. n1 =1145,9 îá/ìèí - ÷àñòîòà âðàùåíèÿ âàëà ÷åðâÿêà. n2 =114,59 îá/ìèí - ÷àñòîòà âðàùåíèÿ âàëà êîëåñà. U=10 – ïåðåäàòî÷íîå ÷èñëî ÷åðâÿ÷íîé ïåðåäà÷è. Ðàñïîëîæåíèå ÷åðâÿêà – íèæíåå. 5.2 Óñòàíîâëåíèå îñíîâíûõ äàííûõ 5.2.1 ×èñëî âèòêîâ ÷åðâÿêà ïðè U=10 ïðèíèìàåì Z1 =10 5.2.2 ×èñëî çóáüåâ ÷åðâÿ÷íîãî êîëåñà ñ îêðóãëåíèåì äî öåëîãî ÷èñëà Z2 =Z1 ⋅U =4⋅10 =40 5.2.3 Óòî÷íåííîå ïðèäàòî÷íîå ÷èñëî r 40 U = 2
= r1 4 5.2.4 ×àñòîòà âðàùåíèÿ âàëà ÷åðâÿ÷íîãî êîëåñà. n 1145,9
u 10 5.2.5 Îðèåíòèðîâî÷íàÿ ñêîðîñòü ñêîëüæåíèÿ â çàöåïëåíèè. Vñê
5.2.6 Âûáîð ïðîôèëÿ ÷åðâÿêà è ìàòåðèàëîâ ÷åðâÿ÷íîé ïàðû. Ïðèíèìàåì àðõèìåäîâ ÷åðâÿê ZA èç ñòàëè 20 ñ öåìåíòàöèåé è çàêàëêîé äî òâåðäîñòè 56 … 63 HRC, âèòêè øëèôîâàííûå è ïîëèðîâàííûå. Ó÷èòûâàÿ, ÷òî Vck < 4ì/ñ, ïî òàáëèöå ïðèíèìàåì â êà÷åñòâå ìàòåðèàëà ÷åðâÿ÷íîãî êîëåñà áåçîëîâÿííóþ áðîíçó ÁðÀ9ÆÇË ñ õàðàêòåðèñòèêàìè: E2 =(0.88...1.14)·105 ÌÏà; v2 =0.35ì/ñ; σT2 =196...343 ÌÏà; σâ2 =490...588 ÌÏà. 5.2.7  ñîîòâåòñòâèè ñ òàáëè÷íûìè äàííûìè ïðè V=2,077 ì/ñ ïðèíèìàåì 8 ñòåïåíü òî÷íîñòè (nT =8) 5.2.8 Îðèåíòèðîâî÷íûé ÊÏÄ ïåðåäà÷è. 0,98 0,98
1 +0,25f⋅u 1 +0,25⋅0,049⋅10 ãäå f=tgϕ=tg2°49’ 39,17” =0,049– ïðèâåäåííûé êîýôôèöèåíò òðåíèÿ â çàöåïëåíèè; φ =3,5-0,92·ln(Vñê )=3,5-0,92·ln(2,077)=20 49’ 39,18” – ïðèâåäåííûé óãîë òðåíèÿ. |
||||||
| ÊÍÓ.ÕÒ.000 ÏÇ | Ëèñò | |||||
| 15 | ||||||
| Èçì. | Ëèñò | ¹ äîêóì. | Ïîäïèñü | Äàòà | ||
5.2.9 Ìîùíîñòü íà âàëó ÷åðâÿêà. T ⋅n 65,356⋅114,59
9550⋅0,901 9550⋅0,873 5.2.10 Êîýôôèöèåíò äèàìåòðà ÷åðâÿêà. q=0,25z2 =0,25⋅40 =10 ïî ÃÎÑÒ 19672-74 5.2.11 Êîýôôèöèåíò íàãðóçêè. K=Kβ ·Kv =1,02·1,14=1,163 Kβ
ðàñïðåäåëåíèÿ íàãðóçêè ïî äëèíå ëèíèè êîíòàêòà â ñëåäñòâèå äåôîðìàöèè ÷åðâÿêà; ⎛ 1 ⎞ ⎛ 1 ⎞ θ
=9⋅(q−4)⋅⎜⎜
1 + z
T t vcp
=
∑
T
Kv =0,3+0,1⋅nT +0,02⋅Vñê =0,3+0,1⋅8+0,02⋅2,077 =1,14 - êîýôôèöèåíò, ó÷èòûâàþùèé äèíàìè÷åñêóþ íàãðóçêó. 5.6 Äîïóñêàåìûå êîíòàêòíûå íàïðÿæåíèÿ. 5.6.1 Äëÿ áåçîëîâÿííîé áðîíçû [σ]H = [σ]H 0 ⋅C V ′ = 300⋅0,823 = 246,9 ãäå [σ]H 0 = 300 ÌÏà – èñõîäíîå äîïóñêàåìîå íàïðÿæåíèå ìàòåðèàëà ÷åðâÿ÷íîãî êîëåñà ïðè øëèôîâàííûõ è ïîëèðîâàííûõ ñ òâåðäîñòüþ HRCý ≥ 45; CV ′ =1 −0.085⋅Vñê =1 −0,085⋅2,077 =0,823 - êîýôôèöèåíò, ó÷èòûâàþùèé âëèÿíèå ñêîðîñòè ñêîëüæåíèÿ íà çàåäàíèå. 5.7 Îïðåäåëåíèå îñíîâíûõ ðàçìåðîâ. 5.7.1 Ìåæîñåâîå ðàññòîÿíèå:
[σ]H 247 5.7.2 Ðàñ÷åòíûé ìîäóëü: 2⋅a 2⋅68
Ïî ÃÎÑÒ 2144-76 ïðèíèìàåì m = 3,15ìì. 5.7.3 Ìåæîñåâîå ðàññòîÿíèå ïðè ñòàíäàðòíûõ çíà÷åíèÿõ m è q:
aw ìì |
|||||
| ÊÍÓ.ÕÒ.000 ÏÇ | Ëèñò | ||||
| 16 | |||||
| Èçì. | Ëèñò | ¹ äîêóì. | Ïîäïèñü | Äàòà | |
5.7.4 Êîýôôèöèåíò ñìåùåíèÿ x 5.7.5 Ãåîìåòðè÷åñêèå ïàðàìåòðû ïåðåäà÷è: ×åðâÿê Äåëèòåëüíûé äèàìåòð: d1 =m⋅q =3,15⋅10 =31,5ìì. Äèàìåòð âåðøèí âèòêîâ: da1 =d1 +2m=31,5+2⋅3,15 =37,8ìì. Äèàìåòð âïàäèí âèòêîâ: df1 =d1 −2,4m=31,5−2,4⋅3,15 =23,94ìì. z 4 Äåëèòåëüíûé óãîë ïîäú¸ìà âèòêà: γ
=arctg 1
=arctg q 10 ⎛ z ⎞ Íà÷àëüíûé óãîë ïîäúåìà âèòêà: γ
w
=arctg⎜⎜
q
Óãîë ïðîôèëÿ âèòêà â íîðìàëüíîì ñå÷åíèè ÷åðâÿêà íà íà÷àëüíîì öèëèíäðå: α nw =arctg(tg20°⋅cosγo =arctg(tg20°⋅cos21ο 48'5,07'') =18°40'19,41'' Äëèíà íàðåçíîé ÷àñòè ÷åðâÿêà: b1 ≥(12,5 +0,09⋅z2 )⋅m=(12,5 +0,09⋅40)⋅3,15 =50,71ìì. ×åðâÿ÷íîå êîëåñî Øèðèíà çóá÷àòîãî âåíöà: z1 =4; b2 ≤0,67⋅da1 =0,67⋅37,8=25,32ìì. Íà÷àëüíûé è äåëèòåëüíûå äèàìåòðû: d2 =dw2 =m⋅z2 =3,15⋅40 =126ìì. Äèàìåòð âåðøèí çóáüåâ: da2 =d2 +2⋅m=126+2⋅3,15 =132,3ìì. Äèàìåòð âïàäèí çóáüåâ: df2 =d2 −2,4m=126−2,4⋅3,15 =118.44ìì. 6⋅m 6⋅3,15 Íàèáîëüøèé äèàìåòð: daM2
≤da2
+ z1 +2 4+2 b 25,32 Óñëîâíûé óãîë îáõâàòà: 2δ
=2⋅arcsin 5.8 Îêðóæíûå ñêîðîñòè. π ⋅d ⋅n π ⋅31,5⋅1145,9
π ⋅d ⋅n π ⋅126⋅114,59
60000 60000 5.9 Ñêîðîñòü ñêîëüæåíèÿ. V 1,889
cosγ w cos21°48'5,07'' |
|||||
| ÊÍÓ.ÕÒ.000 ÏÇ | Ëèñò | ||||
| 17 | |||||
| Èçì. | Ëèñò | ¹ äîêóì. | Ïîäïèñü | Äàòà | |
5.10 Óòî÷íåíèå ÊÏÄ ïåðåäà÷è, êðóòÿùåãî ìîìåíòà è ìîùíîñòè íà ÷åðâÿêå. 5.10.1 ÊÏÄ ÷åðâÿ÷íîãî çàöåïëåíèÿ: tgγ tg21°48'5,07"
tg(γw +ϕ) tg(21°48'5,07"+2°50'48,47'') ϕ=3,5−0,92⋅ln(Vck ) =3,5−0,92⋅ln(2,034) =2°50'48,47''- óòî÷í¸ííûé ïðèâåä¸ííûé óãîë òðåíèÿ 5.10.2 Îáùèé ÊÏÄ ÷åðâÿ÷íîãî ðåäóêòîðà η = η çàö ⋅η ð =0,871⋅0,98=0,854 ãäå ηр = 0,98 – ÊÏÄ ó÷èòûâàþùèé ïîòåðè íà ðàçáðûçãèâàíèå è ïåðåìåøèâàíèÿ ìàñëà. T 65,356 5.10.3 Êðóòÿùèé ìîìåíò íà âàëó ÷åðâÿêà:T1
= 2
= 5.10.4 Ìîùíîñòü íà âàëó ÷åðâÿêà:P1
5.11 Ñèëû â çàöåïëåíèè. 5.11.1 Îêðóæíàÿ ñèëà íà êîëåñå (îñåâàÿ íà ÷åðâÿêå): 2000⋅T 2000⋅65,356
dw2 126 5.11.2 Îêðóæíàÿ ñèëà íà ÷åðâÿêå (îñåâàÿ íà êîëåñå): 2000⋅T 2000⋅7,65
dw1 31,5 5.11.3 Ðàäèàëüíàÿ ñèëà: F r =Ft2 ⋅tgα =1037,39⋅tg20° =377,57Í. 5.12 Ïðîâåðî÷íûé ðàñ÷åò ïî êîíòàêòíûì íàïðÿæåíèÿì. 5.12.1 Êîýôôèöèåíò, ó÷èòûâàþùèé ìåõàíè÷åñêèå ñâîéñòâà ìàòåðèàëîâ:
Çäåñü Å1 è Å2 – ìîäóëè óïðóãîñòè ìàòåðèàëîâ ÷åðâÿêà è âåíöà êîëåñà â ÌÏà v1 è v3 – êîýôôèöèåíòû Ïóàññîíà ìàòåðèàëîâ ÷åðâÿêà è âåíöà ÷åðâÿ÷íîãî êîëåñà |
||||||
| ÊÍÓ.ÕÒ.000 ÏÇ | Ëèñò | |||||
| 18 | ||||||
| Èçì. | Ëèñò | ¹ äîêóì. | Ïîäïèñü | Äàòà | ||
5.12.2 Êîýôôèöèåíò, ó÷èòûâàþùèé ôîðìó ïîâåðõíîñòåé: 2⋅cos2 γ w 2⋅cos2 21°48'5,07''
sin2⋅α nw sin2⋅18°40'19,41'' 5.12.3 Êîýôôèöèåíò, ó÷èòûâàþùèé ñóììàðíóþ äëèíó êîíòàêòíûõ ëèíèé: 1 1
ε α ⋅Kε 1,85⋅0,75 3,9 3,9 ε α =1,95− =1,95− =1,852 - êîýôôèöèåíò òîðöåâîãî ïåðåêðûòèÿ, z2 40 Kε =0,75 - êîýôôèöèåíò èçìåíåíèÿ ñóììàðíîé äëèíû êîíòàêòíûõ ëèíèé. 5.12.4 Êîýôôèöèåíò, ó÷èòûâàþùèé óñëîâíûé óãîë îáõâàòà: 360° 360°
2⋅δ 88°42'52,42'' 5.12.5 Óòî÷íåíèå êîýôôèöèåíòà íàãðóçêè K =Kβ ⋅Kv =1,02⋅1,14=1,162 ãäåK β = 1,02 – êîýôôèöèåíò íåðàâíîìåðíîñòè ðàñïðåäåëåíèÿ íàãðóçêè ïî äëèíå ëèíèè êîíòàêòà, âñëåäñòâèå äåôîðìàöèè ÷åðâÿêà, îñòàëñÿ ïðåæíèì, òàê êàê íå èçìåíèëèñü q è θ , Kv =0,3+0,1⋅nT +0,02⋅Vñê =0,3+0,1⋅8+0,02⋅2,034=1,14 - èçìåíèëàñü ñêîðîñòü ñêîëüæåíèÿ. 5.12.6 Óòî÷íåíèå äîïóñêàåìîãî êîíòàêòíîãî íàïðÿæåíèÿ: [δ]H = [δ]H 0 ⋅CV ′ =300⋅0,827 =248,13ÌÏà , ãäå CV ′ =1 −0,085⋅2,034=0,827 5.12.7 Äåéñòâèòåëüíûå êîíòàêòíûå íàïðÿæåíèÿ: 25,2 K⋅T 25.2 1,162⋅65,356
d2 ddw 1 126 31,5 Óñëîâèå ïðî÷íîñòè ïî êîíòàêòíûì íàïðÿæåíèÿì âûïîëíåíî, ò.ê. σH π [δ]H = 246ÌÏà 5.12.8 Ïðîâåðêà íà ñòàòè÷åñêóþ ïðî÷íîñòü: T
Tíîì [δ]ст =2⋅δ T2 =2⋅270 =540ÌÏà – ïðåäåëüíî äîïóñòèìîå êîíòàêòíîå íàïðÿæåíèå. Ñòàòè÷åñêàÿ ïðî÷íîñòü îáåñïå÷åíà, ò.ê. σНпик < [δ]ст = 540ÌÏà. Óñëîâèÿ ïðî÷íîñòè 5.12.7 è 5.12.8 âûïîëíÿþòñÿ. Ìàòåðèàë êîëåñà îñòàâëÿåì ïðåæíèì. |
||||||
| ÊÍÓ.ÕÒ.000 ÏÇ | Ëèñò | |||||
| 19 | ||||||
| Èçì. | Ëèñò | ¹ äîêóì. | Ïîäïèñü | Äàòà | ||
5.13 Ïðîâåðî÷íûé ðàñ÷åò çóáüåâ êîëåñà íà ïðî÷íîñòü ïðè èçãèáå 5.13.1 Êîýôôèöèåíò, ó÷èòûâàþùèé ñóììàðíóþ äëèíó êîíòàêòíûõ ëèíèé:
Y α ε 5.13.2 Êîýôôèöèåíò, ó÷èòûâàþùèé óñëîâíûé óãîë îáõâàòà: 360° 360°
2⋅δ 88°42'52,42'' 5.13.3 Êîýôôèöèåíò, ó÷èòûâàþùèé íàêëîí çóáà êîëåñà: λ 21°48'5,07''
140° 140° 5.13.4 Êîýôôèöèåíò ôîðìû çóáà: z 40
cosγ cos21°48'5,07'' êîýôôèöèåíò ôîðìû çóáà áóäåò YF =2,19. 5.13.5 Óñëîâíûé áàçîâûé ïðåäåë èçãèáíîé âûíîñëèâîñòè çóáüåâ êîëåñà äëÿ áðîíç ïðè íåðåâåðñèâíîé íàãðóçêå: δ F0 =0,14⋅δ â2 +0,44⋅δ T2 =0,14⋅540+0,44⋅270 =194,4ÌÏà. 5.13.6 Êîýôôèöèåíò ðåæèìà:
5.13.7 Ýêâèâàëåíòíîå ÷èñëî öèêëîâ: NFE =25⋅107 5.13.7 Êîýôôèöèåíò äîëãîâå÷íîñòè:
NFE 25⋅10 5.13.8 Äîïóñêàåìîå íàïðÿæåíèå èçãèáà:
[δ]F
= SF ãäå S F =1,75- êîýôôèöèåíò áåçîïàñíîñòè. |
||||||
| ÊÍÓ.ÕÒ.000 ÏÇ | Ëèñò | |||||
| 20 | ||||||
| Èçì. | Ëèñò | ¹ äîêóì. | Ïîäïèñü | Äàòà | ||
5.13.9 Íàïðÿæåíèå èçãèáà â çóáüÿõ: F ⋅K 1037⋅1,73 δ
F
=Yε
⋅Yδ
⋅Yγ
⋅YF
⋅ π ⋅dw1 ⋅m π ⋅31,5⋅3,15 σF < [δ]F 0 = 60,32ÌÏà. 5.13.10 Ïðîâåðî÷íûé ðàñ÷åò çóáüåâ êîëåñà íà ñòàòè÷åñêóþ ïðî÷íîñòü ïðè èçãèáå: T δ Fïïè = δ F ⋅ max =28,87⋅2,2 =63,52 ÌÏà – äåéñòâèòåëüíîå ïèêîâîå íàïðÿæåíèå Tíîì [δ]Нст = 0,8⋅δT 2 =0.8⋅270 =216ÌÏà – ïðåäåëüíî äîïóñòèìîå íàïðÿæåíèå èçãèáà. σFппи π [ ]σ Fсста = 216ÌÏà Óñëîâèÿ ïðî÷íîñòè 5.13.10 è 5.13.11 âûïîëíÿþòñÿ. Ìàòåðèàë êîëåñà îñòàâëÿåì ïðåæíèì. 5.14 Òåïëîâîé ðàñ÷åò 5.14.1 Òåìïåðàòóðà ìàñëà ïðè óñòàíîâèâøåìñÿ ðåæèìå: 1000⋅P ⋅(1 − η)
1000⋅1,087⋅(1 −0,854) tóñò
=t0
+ k⋅A⋅(1 + ψ) 15⋅0,125⋅(1 +0,3) t0 =20°Ñ - òåìïåðàòóðà îêðóæàþùåé ñðåäû; k=15Âò/(ì2 ãðàäóñ) – êîýôôèöèåíò òåïëîîòäà÷è; A≈20⋅aw 2 =20⋅0,0792 =0,125ì2 – ñâîáîäíàÿ ïîâåðõíîñòü îõëàæäåíèÿ êîðïóñà ðåäóêòîðà; ψ =0.3- êîýôôèöèåíò, ó÷èòûâàþùèé òåïëîîòâîä â ôóíäàìåíòàëüíóþ ïëèòó èëè ðàìó ìàøèíû. Òåìïåðàòóðíûé ðåæèì óäîâëåòâîðèòåëüíûé. 5.15 Ðàñ÷åò ÷åðâÿêà íà æåñòêîñòü. Ðàññòîÿíèå ìåæäó ñåðåäèíàìè îïîð âàëà ÷åðâÿêà ïðè ïðèáëèæåííîì ðàñ÷åòå ìîæíî ïðèíèìàòü ðàâíûì: L = 0.95⋅d2 = 0.95⋅126 = 119,7 ìì Ïðàâèëüíîñòü çàöåïëåíèÿ ÷åðâÿ÷íîé ïàðû ìîæåò áûòü îáåñïå÷åíà ëèøü ïðè äîñòàòî÷íîé æåñòêîñòè ÷åðâÿêà. Ñðåäíÿÿ äîïóñêàåìàÿ ñòðåëà ïðîãèáà [f] ÷åðâÿêà ìîæåò áûòü ïðèíÿòà:
Ñòðåëà ïðîãèáà ÷åðâÿêà, âàë êîòîðîãî îïèðàåòñÿ íà äâà ðàäèàëüíî-óïîðíûõ ïîäøèïíèêà îïðåäåëÿåòñÿ ïî ôîðìóëå:
48EJïð ãäå E = 2.1 10. 5 МПа L – ðàññòîÿíèå ìåæäó ñåðåäèíàìè îïîð; Jïð – ïðèâåäåííûé ìîìåíò èíåðöèè ñå÷åíèÿ ÷åðâÿêà, îïðåäåëÿåìûé ïî ýìïèðè÷åñêîé ôîðìóëå: πdf 4 1 da1 π•23,944 37,8 4
|
||||||
| ÊÍÓ.ÕÒ.000 ÏÇ | Ëèñò | |||||
| 21 | ||||||
| Èçì. | Ëèñò | ¹ äîêóì. | Ïîäïèñü | Äàòà | ||
Íàéäåì ðåàëüíóþ ñòðåëó ïðîãèáà:
f < [f], ñëåäîâàòåëüíî, óñëîâèå æåñòêîñòè âûïîëíÿåòñÿ. |
|||||
| ÊÍÓ.ÕÒ.000 ÏÇ | Ëèñò | ||||
| 22 | |||||
| Èçì. | Ëèñò | ¹ äîêóì. | Ïîäïèñü | Äàòà | |
6.ÏÐÎÅÊÒÍÛÉ ÐÀÑ×ÅÒ ÂÀËΠÐÅÄÓÊÒÎÐÀ È ÏÎÄÁÎÐ ÏÎÄØÈÏÍÈÊÎÂ. Ðàññ÷èòàåì âõîäíîé è âûõîäíîé âàëû. Èç ïðåäûäóùèõ ðàñ÷åòîâ ðåäóêòîðà èçâåñòíî: à) ìîìåíòû ïåðåäàâàåìûå âàëàìè ÒI = 7.689 Í⋅ì è ÒII = 65.356 Í⋅ì; á) äèàìåòðû d1 = 31,5 ìì è d2 = 126 ìì; 6.1. Âõîäíîé âàë ÷åðâÿ÷íîãî ðåäóêòîðà. 6.1.1. Âûáîð ìàòåðèàëà âàëà. Íàçíà÷àåì ìàòåðèàë âàëà – ÁðÀ9Æ3Ë: σ = 500 ÌÏà, σÒ = 230 ÌÏà. 6.1.2. Ïðîåêòíûé ðàñ÷åò âàëà. Ïðèáëèæåííî îöåíèì äèàìåòð êîíñîëüíîãî ó÷àñòêà âàëà ïðè [τ]=20 ÌÏà. T 7,689•1000
0,2[ ]τk 0.2•20 Ïî ñòàíäàðòíîìó ðÿäó ïðèíèìàåì dâ =12 ìì, òîãäà t =2 ìì, r = 1.6 ìì, f =1. 6.1.3. Îïðåäåëèì äèàìåòðû ó÷àñòêîâ âàëà. Äèàìåòðû ïîäøèïíèêîâûõ øååê: dï1 = dâ +2⋅t = 12 +2⋅2 = 16 ìì; ïðèíèìàåì dï1 = 17 ìì 6.2. Âûõîäíîé âàë. 6.2.1. Âûáîð ìàòåðèàëà âàëà. Âûáåðåì ñòàëü 40Õ 6.2.2. Ïðèáëèæåííî îöåíèì äèàìåòð âûõîäíîãî êîíöà âàëà ïðè [τ] = 30 ÌÏà. Ò 65.356•1000
0,2• [ ]τ 0,2•30 Ïî ñòàíäàðòíîìó ðÿäó ïðèíèìàåì dâ =20 ìì 6.2.3. Îïðåäåëèì äèàìåòðû ó÷àñòêîâ âàëà. Äèàìåòðû ïîäøèïíèêîâûõ øååê: dï2 = dâ +2⋅t = 20+2⋅2 = 24 ìì; Çíà÷åíèÿ dï äîëæíû áûòü êðàòíû 5, ïîýòîìó ïðèíèìàåì dï2 = 25 ìì dáï2 = dï2 +3,2⋅r = 24+3,2⋅1,6 = 29ìì Ïî ñòàíäàðòíîìó ðÿäó ïðèíèìàåì dáï2 = 30 ìì Çäåñü t = 2 ìì, r = 1,6 ìì, f = 1 Äèàìåòð ñòóïèöû ÷åðâÿ÷íîãî êîëåñà: dñò2 = (1.6…1.8)dáï2 = (1.6…1.8)⋅30 = 48…54 (ìì) Ïðèíèìàåì dñò2 = 50ìì. |
|||||
| ÊÍÓ.ÕÒ.000 ÏÇ | Ëèñò | ||||
| 23 | |||||
| Èçì. | Ëèñò | ¹ äîêóì. | Ïîäïèñü | Äàòà | |
Äëèíà ñòóïèöû ÷åðâÿ÷íîãî êîëåñà: lñò2 = (1.2…1.8)dáï2 = (1.2…1.8)⋅30 = 36…54 (ìì) Ïðèíèìàåì lñò2 = 40 ìì. 6.3. Ïîäáîð ïîäøèïíèêîâ. 6.3.1.Ïîäáîð ïîäøèïíèêîâ äëÿ ÷åðâÿêà. Äëÿ ÷åðâÿêà ïðèìåì ïðåäâàðèòåëüíî ïîäøèïíèêè ðîëèêîâûå êîíè÷åñêèå 7205 ëåãêîé ñåðèè. Ñõåìà óñòàíîâêè ïîäøèïíèêîâ – âðàñïîð. Èç òàáëèöû âûïèñûâàåì: d = 25 ìì, D = 52 ìì, Ò = 16,5 ìì, e = 0.36. Ñìåùåíèå òî÷êè ïðèëîæåíèÿ ðàäèàëüíîé ðåàêöèè îò òîðöà ïîäøèïíèêà: T (d +D)e 16,5 (25+52)•0,36
2 6 2 6 6.3.2.Ïîäáîð ïîäøèïíèêîâ äëÿ âàëà ÷åðâÿ÷íîãî êîëåñà. Äëÿ âàëà ÷åðâÿ÷íîãî êîëåñà ïðèìåì øàðèêîïîäøèïíèêè ðàäèàëüíî-óïîðíûå 46303 ñðåäíåé ñåðèè. Èç òàáëèöû âûïèñûâàåì: d = 17 ìì, D = 47 ìì,  = 14 ìì, α = 260 Ñìåùåíèå òî÷êè ïðèëîæåíèÿ ðàäèàëüíîé ðåàêöèè îò òîðöà ïîäøèïíèêà: a1 =0,5{B+0,5(D+d)tgα} =0,5{14+0,5•(47 +17)tg200 ) = 15 ìì |
||||||
| ÊÍÓ.ÕÒ.000 ÏÇ | Ëèñò | |||||
| 24 | ||||||
| Èçì. | Ëèñò | ¹ äîêóì. | Ïîäïèñü | Äàòà | ||
7.ÊÎÍÑÒÐÓÊÒÈÂÍÛÅ ÐÀÇÌÅÐÛ ×ÅÐÂßÊÀ È ×ÅÐÂß×ÍÎÃÎ ÊÎËÅÑÀ. 7.1.Ðàçìåðû ÷åðâÿêà. ×åðâÿê âûïîëíÿåì çà îäíî öåëîå ñ âàëîì. Ðàçìåðû âàëà è ÷åðâÿêà áûëè îïðåäåëåíû ðàíåå, ïîýòîìó òîëüêî âûïèøåì èõ äëÿ óäîáíîãî äàëüíåéøåãî èñïîëüçîâàíèÿ: - äèàìåòð äåëèòåëüíîé îêðóæíîñòè d1 = 31,5 ìì; - äèàìåòð âåðøèí da1 = 37,8 ìì; - äèàìåòð âïàäèí df1 = 23,9 ìì; - äëèíà íàðåçàííîé ÷àñòè ÷åðâÿêà b1 = 50,7 ìì; - äèàìåòð âàëà dáï1 = 17 ìì. 7.2.Ðàñ÷åò êîíñòðóêòèâíûõ ðàçìåðîâ ÷åðâÿ÷íîãî êîëåñà. Îñíîâíûå ãåîìåòðè÷åñêèå ðàçìåðû ÷åðâÿ÷íîãî êîëåñà áûëè íàìè îïðåäåëåíû ðàíåå. Äëÿ óäîáñòâà äàëüíåéøåãî èñïîëüçîâàíèÿ âûïèøåì èõ: - äèàìåòð äåëèòåëüíîé îêðóæíîñòè d2 = 126 ìì; - äèàìåòð âåðøèí da2 = 132,3 ìì; - äèàìåòð âïàäèí df2 = 118,4 ìì; - øèðèíà âåíöà ÷åðâÿ÷íîãî êîëåñà b2 = 25,3 ìì; - äèàìåòð îòâåðñòèÿ ïîä âàë d = 30 ìì; - äèàìåòð ñòóïèöû ÷åðâÿ÷íîãî êîëåñà dñò2 = 50 ìì; -äëèíà ñòóïèöû ÷åðâÿ÷íîãî êîëåñà lñò2 = 40 ìì. Êîëåñî êîíñòðóèðóåì îòäåëüíî îò âàëà. Èçãîòîâèì ÷åðâÿ÷íîå êîëåñî ñîñòàâíûì): öåíòð êîëåñà èç ñåðîãî ÷óãóíà, çóá÷àòûé âåíåö – èç áðîíçû ÁðÀ9ÆÇË. Ñîåäèíèì çóá÷àòûé âåíåö ñ öåíòðîì ïîñàäêîé ñ íàòÿãîì. Òàê êàê ó íàñ íàïðàâëåíèå âðàùåíèÿ ïîñòîÿííîå, òî íà íàðóæíîé ïîâåðõíîñòè öåíòðà ñäåëàåì áóðòèê. Òàêàÿ ôîðìà öåíòðà ÿâëÿåòñÿ òðàäèöèîííîé. Îäíàêî íàëè÷èå áóðòèêà óñëîæíèò èçãîòîâëåíèå è öåíòðà, è âåíöà. ×åðâÿ÷íîå êîëåñî âðàùàåòñÿ ñ íåáîëüøîé ñêîðîñòüþ, ïîýòîìó íåðàáî÷èå ïîâåðõíîñòè îáîäà, äèñêà, ñòóïèöû êîëåñà îñòàâëÿåì íåîáðàáîòàííûìè è äåëàåì êîíóñíûìè ñ áîëüøèìè ðàäèóñàìè çàêðóãëåíèé. Îñòðûå êðîìêè íà òîðöàõ âåíöà ïðèòóïëÿåì ôàñêàìè f ≈ 0.5m, ãäå m – ìîäóëü çàöåïëåíèÿ. f = 0,5⋅3,15 = 1,6 ìì Ðàññ÷èòàåì îñíîâíûå êîíñòðóêòèâíûå ýëåìåíòû êîëåñà: Ñ = 0,25b2 = 0,25⋅25,3 = 6 ìì; δ 1 = δ 2 = 2m = 2⋅3,15 = 6,3 ìì; |
||||||
| ÊÍÓ.ÕÒ.000 ÏÇ | Ëèñò | |||||
| 25 | ||||||
| Èçì. | Ëèñò | ¹ äîêóì. | Ïîäïèñü | Äàòà | ||
8.ÐÀÑ×ÅÒ ÝËÅÌÅÍÒΠÊÎÐÏÓÑÀ ÐÅÄÓÊÒÎÐÀ. 8.1. Òîëùèíà ñòåíêè êîðïóñà è êðûøêè ÷åðâÿ÷íîãî ðåäóêòîðà: δ =0,04a + 2 = 0,04 · 79 + 2 = 5,16 ìì ïðèíèìàåì δ = 8 ìì; δ 1 = 0,032à + 2 = 0,032 · 79 + 2 = 4,53 ìì, ïðèíèìàåì δ = 8 ìì. 8.2. Òîëùèíà ôëàíöåâ êîðïóñà è êðûøêè: b = b1 = 1,5δ = 1,5 · 8 = 12 ìì 8.3.Òîëùèíà íèæíåãî ïîÿñà êîðïóñà ïðè íàëè÷èè áîáûøåê: ð1 = 1,5δ = 1,5 · 8 = 12 ìì; ð2 = (2,25 ÷ 2,75)δ = (2,25 ÷ 2,75) · 8 = 18…22 ìì; ïðèíèìàåì ð2 = 20 ìì; 8.4.Òîëùèíà ðåáåð îñíîâàíèÿ êîðïóñà è êðûøêè: m = m1 = (0,85 ÷ 1)δ = 6,8…8 ìì 8.5.Äèàìåòð ôóíäàìåíòíûõ áîëòîâ: d1 = (0,03 ÷ 0,036)a + 12 = (0,03 ÷ 0,036) · 79 + 12 = 14,4…15 ìì, ïðèíèìàåì áîëòû ñ ðåçüáîé Ì16; 8.6.Äèàìåòð áîëòîâ: ó ïîäøèïíèêîâ: d2 = (0,7 ÷ 0,75)d1 = (0,7 ÷ 0,75) · 16 = 11,2…12 ìì ïðèíèìàåì áîëòû ñ ðåçüáîé Ì8 ñîåäèíÿþùèõ îñíîâàíèå êîðïóñà ñ êðûøêîé: d3 = (0,5 ÷ 0,6)d1 = (0,5 ÷ 0,6) · 16 = 8…10 ìì ïðèíèìàåì áîëòû ñ ðåçüáîé Ì10; 8.7.Ðàçìåð øòèôòà: äèàìåòð: dø = d3 ïðèíèìàåì dø = 8 ìì äëèíà: lø = b + b1 + 5 ìì = 12 + 12 + 5 = 29 ìì ïðèíèìàåì äëèíó øòèôòà l = 30 ìì |
||||||
| ÊÍÓ.ÕÒ.000 ÏÇ | Ëèñò | |||||
| 26 | ||||||
| Èçì. | Ëèñò | ¹ äîêóì. | Ïîäïèñü | Äàòà | ||
9.Ïðîâåðêà äîëãîâå÷íîñòè ïîäøèïíèêîâ Âåäîìûé âàë Ðàññòîÿíèå ìåæäó îïîðàìè (òî÷íåå, ìåæäó òî÷êàìè ïðèëîæåíèÿ ðàäèàëüíûõ ðåàêöèé R3 è R4 ) l2 = 70 ìì; äèàìåòð d2 = 126 ìì.
9.1 Îïîðíûå ðåàêöèè â ïëîñêîñòè xz: 1038
2 9.2 Îïîðíûé ðåàêöèè â ïëîñêîñòè yz: R4yl2 + Frl2 - Fad2 = 0; 2 2 l d -F r 2 + F a 2 -377,57•35+485,71•63
R3yl2 – Frl2 - Fad2 = 0; 2 2 l d F r 2 + F a 2 377,57•35+48571, •63 R3y
= 2 2
= Ïðîâåðêà: ∑Fy = - R3y – Fr – R4y = - 625,92 + 377,57 + 248,35 = 0 |
|||||
| ÊÍÓ.ÕÒ.000 ÏÇ | Ëèñò | ||||
| 27 | |||||
| Èçì. | Ëèñò | ¹ äîêóì. | Ïîäïèñü | Äàòà | |
9.3 Ñóììàðíûå ðåàêöèè: Fr3 = R3 = R3 2 x +R3 2 y = 5192 +6252 = 813 H
9.4 Îñåâûå ñîñòàâëÿþùèå ðàäèàëüíûõ ðåàêöèé êîíè÷åñêèõ ïîäøèïíèêîâ: S3 = 0,83eFr3 = 0,83 · 0,360 · 813 = 243 H S4 = 0,83eFr3 = 0,83 · 0,360 · 575 = 172 H e = 0,360 – êîýôôèöèåíò âëèÿíèÿ îñåâîãî íàãðóæåíèÿ 9.5 Îñåâûå íàãðóçêè ïîäøèïíèêîâ: S3 ≥ S4 ; Fa = 0; S3 < S4 ; Fa > S4 – S3 Fa3 = S3 = 243 H; Fa4 = S3 + Fa = 243 + 486 = 729 H. «3» ïîäøèïíèê:
Fr3 813 Ýêâèâàëåíòíàÿ íàãðóçêà: Pý3 = Fr3 VKá KT = 813 · 1 · 1,2 · 1 = 975,6 H. ãäå, V – êèíåìàòè÷åñêèé êîýôôèöèåíò; Ká – êîýôôèöèåíò äèíàìè÷íîñòè íàãðóçêè èëè êîýôôèöèåíò áåçîïàñíîñòè; KT – êîýôôèöèåíò âëèÿíèÿ òåìïåðàòóðû ïîäøèïíèêà íà åãî äîëãîâå÷íîñòü. «4» ïîäøèïíèê:
Fr4 575 Pý4 = (XVFr3 + YFa ) · Ká KT = (0,4 · 1 · 575 + 1,666 · 729) · 1,2 · 1 = 1,73 êÍ. Ká = 1,2 – êîýôôèöèåíò áåçîïàñíîñòè; KÒ = 1,0 – òåìïåðàòóðíûé êîýôôèöèåíò; Õ – êîýôôèöèåíò ðàäèàëüíîé íàãðóçêè; V – êîýôôèöèåíò âðàùåíèÿ îòíîñèòåëüíîãî âåêòîðà íàãðóçêè âíóòðåííåãî êîëüöà ïîäøèïíèêà. |
|||||
| ÊÍÓ.ÕÒ.000 ÏÇ | Ëèñò | ||||
| 28 | |||||
| Èçì. | Ëèñò | ¹ äîêóì. | Ïîäïèñü | Äàòà | |
Äîëãîâå÷íîñòü îïðåäåëÿþ äëÿ «4» ïîäøèïíèêà, ò.å. äëÿ ïîäøèïíèêà ó êîòîðîãî ýêâèâàëåíòíàÿ íàãðóçêà çíà÷èòåëüíî áîëüøå. 9.6 Ðåñóðñ ïîäøèïíèêà: L = (C/Pý4 )m = (23,4/1,733)3,33 = 5811 ìëí. îá. m =3.33 – ïîêàçàòåëü êðèâîé âûíîñëèâîñòè. L•106 5811•106
60•n 60•114,59 |
||||||
| ÊÍÓ.ÕÒ.000 ÏÇ | Ëèñò | |||||
| 29 | ||||||
| Èçì. | Ëèñò | ¹ äîêóì. | Ïîäïèñü | Äàòà | ||
10. ÏÐÎÂÅÐÊÀ ÏÐÎ×ÍÎÑÒÈ ØÏÎÍÎ×ÍÎÃÎ ÑÎÅÄÈÍÅÍÈß È ÏÎÑÀÄÊÈ ÂÅÍÖÀ ×ÅÐÂß×ÍÎÃÎ ÊÎËÅÑÀ. 10.1. Ðàññ÷èòàåì øïîíî÷íîå ñîåäèíåíèå äëÿ âõîäíîãî âàëà ñ øêèâîì. Øïîíêó âûáèðàåì ïðèçìàòè÷åñêóþ ïî ÃÎÑÒ 23360-78. Ðàçìåðû øïîíêè: - ñå÷åíèå b × h = 5 × 5 ìì; - ãëóáèíà ïàçà âàëà t1 = 3 ìì; - ãëóáèíà ïàçà ñòóïèöû t2 = 2,3 ìì; - äëèíà l = 32 ìì. Øïîíêà ïðèçìàòè÷åñêàÿ ñî ñêðóãëåííûìè òîðöàìè. Ìàòåðèàë øïîíêè – ñòàëü 45 íîðìàëèçîâàííàÿ. Íàïðÿæåíèÿ ñìÿòèÿ è óñëîâèÿ ïðî÷íîñòè îïðåäåëÿåì ïî ôîðìóëå: 2Т σсм = d(h − t1)⋅l Ïðè ÷óãóííîé ñòóïèöå [σ]ñì = 70…100 ÌÏà. Ïåðåäàâàåìûé ìîìåíò Ò = 7,689 Í⋅ì. 2Ò 2• 7.689 •1000
σñì < [σ]ñì , ñëåäîâàòåëüíî, äîïóñòèìî óñòàíîâèòü øêèâ èç ÷óãóíà Ñ×32 10.2.Ðàññ÷èòàåì øïîíî÷íûå ñîåäèíåíèÿ äëÿ âûõîäíîãî âàëà. 10.2.1.Ñîåäèíåíèå âàë-êîëåñî. Øïîíêó âûáèðàåì ïðèçìàòè÷åñêóþ ïî ÃÎÑÒ 23360-78. Ðàçìåðû øïîíêè: - ñå÷åíèå b × h = 10 × 8 ìì; - ãëóáèíà ïàçà âàëà t1 = 5 ìì; - ãëóáèíà ïàçà ñòóïèöû t2 = 3,3 ìì; - äëèíà l = 32 ìì. Øïîíêà ïðèçìàòè÷åñêàÿ ñî ñêðóãëåííûìè òîðöàìè. Ìàòåðèàë øïîíêè – ñòàëü 45 íîðìàëèçîâàííàÿ. Íàïðÿæåíèÿ ñìÿòèÿ è óñëîâèÿ ïðî÷íîñòè îïðåäåëÿåì ïî ôîðìóëå: 2Т
Ïðè ÷óãóííîì öåíòðå êîëåñà [σ]ñì = 70…100 ÌÏà. Ïåðåäàâàåìûé ìîìåíò Ò = 65,356 Í⋅ì. 2Ò 2• 65.356 •1000
σñì < [σ]ñì , ñëåäîâàòåëüíî, äîïóñòèìî öåíòð ÷åðâÿ÷íîãî êîëåñà èçãîòîâèòü èç ñåðîãî ÷óãóíà Ñ×20 |
||||||
| ÊÍÓ.ÕÒ.000 ÏÇ | Ëèñò | |||||
| 30 | ||||||
| Èçì. | Ëèñò | ¹ äîêóì. | Ïîäïèñü | Äàòà | ||
10.2.2.Ñîåäèíåíèå âàëà ñ èñïîëíèòåëüíûì ìåõàíèçìîì: 10.2.3. Øïîíêó âûáèðàåì ïðèçìàòè÷åñêóþ ïî ÃÎÑÒ 23360-78. Ðàçìåðû øïîíêè: 2Ò 2• 65.356 •1000
d(h-t1)(l- b) 20(6-3.5)(45 - 6) - ñå÷åíèå b × h = 6 × 6 ìì; - ãëóáèíà ïàçà âàëà t1 = 3,5 ìì; - ãëóáèíà ïàçà t2 = 2,8 ìì; 2Т σсм = d(h − t1)⋅l - äëèíà l = 45 ìì. Øïîíêà ïðèçìàòè÷åñêàÿ ñî ñêðóãëåííûìè òîðöàìè. Ìàòåðèàë øïîíêè – ñòàëü 45 íîðìàëèçîâàííàÿ. Íàïðÿæåíèÿ ñìÿòèÿ è óñëîâèÿ ïðî÷íîñòè îïðåäåëÿåì ïî ôîðìóëå: Ïðè ÷óãóííîé ñòóïèöå [σ]ñì = 70…100 ÌÏà. Ïåðåäàâàåìûé ìîìåíò Ò = 65,356 Í⋅ì. σñì < [σ]ñì |
||||||
| ÊÍÓ.ÕÒ.000 ÏÇ | Ëèñò | |||||
| 31 | ||||||
| Èçì. | Ëèñò | ¹ äîêóì. | Ïîäïèñü | Äàòà | ||
11. ÂÛÁÎÐ ÑÌÀÇÊÈ ÐÅÄÓÊÒÎÐÀ È ÓÏËÎÒÍÈÒÅËÜÍÛÕ ÓÑÒÐÎÉÑÒÂ. 11.1 Âûáîð ñèñòåìû è âèäà ñìàçêè. Ïðè ñêîðîñòè ñêîëüæåíèÿ â çàöåïëåíèè VS =2,034 ì/ñ, ðåêîìåíäóåìàÿ âÿçêîñòü ν 50 = 266 ñÑò. Ïî ÃÎÑÒó íåôòåïðîäóêòîâ ïðèíèìàþ ìàñëî òðàíñìèññèîííîå ÒÀÄ-17è(ÃÎÑÒ 23652-79). Èñïîëüçóåì êàðòåðíóþ ñèñòåìó ñìàçûâàíèÿ.  êîðïóñ ðåäóêòîðà çàëèâàåì ìàñëî, íà âûñîòó âèòêà, íî íå âûøå öåíòðà òåëà êà÷åíèÿ ïîäøèïíèêà. Ïðè âðàùåíèè êîëåñà ìàñëî áóäåò óâëåêàòüñÿ åãî çóáüÿìè, ðàçáðûçãèâàòüñÿ, ïîïàäàòü íà âíóòðåííèå ñòåíêè êîðïóñà, îòêóäà ñòåêàòü â íèæíþþ åãî ÷àñòü. Âíóòðè êîðïóñà îáðàçóåòñÿ âçâåñü ÷àñòèö ìàñëà â âîçäóõå, êîòîðûì ïîêðûâàþòñÿ ïîâåðõíîñòè ðàñïîëîæåííûõ âíóòðè êîðïóñà äåòàëåé, â òîì ÷èñëå è ïîäøèïíèêè. Îáúåì ìàñëÿíîé âàííû V = 0,75 ë. 11.2 Âûáîð óïëîòíåíèé. È äëÿ ÷åðâÿêà, è äëÿ ÷åðâÿ÷íîãî êîëåñà âûáåðåì ìàíæåòíûå óïëîòíåíèÿ ïî ÃÎÑÒ 8752-79. Óñòàíîâèì èõ ðàáî÷åé êðîìêîé âíóòðü êîðïóñà òàê, ÷òîáû îáåñïå÷èòü ê íåé õîðîøèé äîñòóï ìàñëà. |
||||||
| ÊÍÓ.ÕÒ.000 ÏÇ | Ëèñò | |||||
| 32 | ||||||
| Èçì. | Ëèñò | ¹ äîêóì. | Ïîäïèñü | Äàòà | ||
12. Ñáîðêà ðåäóêòîðà Ïåðåä ñáîðêîé âíóòðåííþþ ïîëîñòü êîðïóñà òùàòåëüíî î÷èùàþò è ïîêðûâàþò ìàñëîñòîéêîé êðàñêîé. Ñáîðêó ðåäóêòîðà ïðîèçâîäÿò â ñîîòâåòñòâèè ñ ÷åðòåæîì îáùåãî âèäà. Íà÷èíàþò ñáîðêó ñ òîãî, ÷òî íà ÷åðâÿ÷íûé âàë 0 íàäåâàþò êðûëü÷àòêè è ðàäèàëüíî-óïîðíûå ïîäøèïíèêè, ïðåäâàðèòåëüíî íàãðåâ èõ â ìàñëå äî 80-100Ñ. Ñîáðàííûé ÷åðâÿ÷íûé âàë âñòàâëÿþò â êîðïóñ. âàëà; çàòåì íàäåâàþò ðàñïîðíóþ âòóëêó è óñòàíàâëèâàþ Âíà÷àëå ñáîðêè âàëà ÷åðâÿ÷íîãî êîëåñà çàêëàäûâàþò øïîíêó è íàïðåññîâûâàþò êîëåñî äî óïîðà â áóðò ò ðîëèêîâûå êîíè÷åñêèå ïîäøèïíèêè, íàãðåòûå â ìàñëå. ïîâåðõíîñòè ñòûêà ôëàíöåâ ñïèðòîâûì ëàêîì. Äëÿ öÑîáðàííûé âàë óêëàäûâàþò â îñíîâàíèå êîðïóñà è íàäåâàþåíòðîâêè êðûøêó óñòàíàâëèâàþò íà êîðïóñ ñ ïîìîùüþ äâóõ ò êðûøêó êîðïóñà, ïîêðûâàÿ ïðåäâàðèòåëüíî êîíè÷åñêèõ øòèôòîâ è çàòÿãèâàþò áîëòû. Çàêëàäûâàþò â ïîäøèïíèêîâûå ñêâîçíûå êðûøêè ðåçèíîâûå ìàíæåòû è óñòàíàâëèâàþò êðûøêè ñ ïðîêëàäêàìè. Ââåðòûâàþò ïðîáêó ìàñëîñïóñêíîãî îòâåðñòèÿ ñ ïðîêëàäêîé è ìàñëîóêàçàòåëü. Çàëèâàþò â ðåäóêòîð ìàñëî è çàêðûâàþò ñìîòðîâîå îòâåðñòèå êðûøêîé. Ñîáðàííûé ðåäóêòîð îáêàòûâàþò è èñïûòûâàþò íà ñòåíäå â ñîîòâåòñòâèè ñ òåõíè÷åñêèìè óñëîâèÿìè. |
||||||
| ÊÍÓ.ÕÒ.000 ÏÇ | Ëèñò | |||||
| 33 | ||||||
| Èçì. | Ëèñò | ¹ äîêóì. | Ïîäïèñü | Äàòà | ||
Ïðèëîæåíèå |
||||
| ÊÍÓ.ÕÒ.000 ÏÇ | Ëèñò | |||
| 34 | ||||
| Èçì. | Ëèñò | ¹ äîêóì. | Ïîäïèñü | Äàòà |
| Îáîçíà÷åíèå | Íàèìåíîâàíèå | Êîë. | Ïðèìå- ÷àíèå |
|||||||||
| Äîêóìåíòàöèÿ | ||||||||||||
| ÊÍÓ.ÕÒ.000 Ñ | Á | Ñáîðî÷íûé ÷åðòåæ | ||||||||||
| ÊÍÓ.ÕÒ.000 Ï | Ç | Ïîÿñíèòåëüíàÿ çàïèñêà | ||||||||||
| Ñáîðî÷íûå åäèíèöû | ||||||||||||
| 1 | ÊÍÓ.ÕÒ.101 | Êîëåñî ÷åðâÿ÷íîå | 1 | |||||||||
| 2 | ÊÍÓ.ÕÒ.102 | Ìàñëîóêàçàòåëü | 1 | |||||||||
| Äåòàëè | ||||||||||||
| 3 | ÊÍÓ.ÕÒ.103 | Êîðïóñ | 1 | |||||||||
| 4 | ÊÍÓ.ÕÒ.104 | Êðûøêà êîðïóñà | 1 | |||||||||
| 5 | ÊÍÓ.ÕÒ.105 | Âàë | 1 | |||||||||
| 6 | ÊÍÓ.ÕÒ.106 | ×åðâÿê | 1 | |||||||||
| 7 | ÊÍÓ.ÕÒ.107 | Âòóëêà | 1 | |||||||||
| 8 | ÊÍÓ.ÕÒ.108 | Êîëüöî | 1 | |||||||||
| 9 | ÊÍÓ.ÕÒ.109 | Êðûøêà ëþêà | 1 | |||||||||
| 10 | ÊÍÓ.ÕÒ.110 | Êðûøêà ïîäøèïíèêà | 1 | |||||||||
| 11 | ÊÍÓ.ÕÒ.111 | Êðûøêà ïîäøèïíèêà | 1 | |||||||||
| 12 | ÊÍÓ.ÕÒ.112 | Ïðîêëàäêà ðåãóëèðîâî÷íàÿ | 6 | |||||||||
| 13 | ÊÍÓ.ÕÒ.113 | Ïðîêëàäêà ðåãóëèðîâî÷íàÿ | 5 | |||||||||
| 14 | ÊÍÓ.ÕÒ.114 | Ïðîêëàäêà óïëîòíèòåëüíàÿ | 1 | |||||||||
| 15 | ÊÍÓ.ÕÒ.115 | Ïðîêëàäêà óïëîòíèòåëüíàÿ | 1 | |||||||||
| 16 | ÊÍÓ.ÕÒ.116 | Ñòàêàí | 1 | |||||||||
| 17 | ÊÍÓ.ÕÒ.117 | Ñòàêàí | 1 | |||||||||
| 18 | ÊÍÓ.ÕÒ.118 | Ïðîáêà | 1 | |||||||||
| ÊÍÓ.ÕÒ.000 ÑÏ | ||||||||||||
| Èçì | Ëèñò | ¹ äîêóìåíòà | Ïîäïèñü | Äàòà | ||||||||
| Ðàçðàá. | Äæåíëîäà Ð.Õ. | Ðåäóêòîð ÷åðâÿ÷íûé | Ëèò. | Ëèñò | Ëèñòîâ | |||||||
| Ïðîâ. | Öîé Ó.À. | ó | 1 | 2 | ||||||||
ÊÍÓ ãðóïïà ÕÒ – 01 |
||||||||||||
| Í. êîíòð. | ||||||||||||
| Óòâ | ||||||||||||
| Îáîçíà÷åíèå | Íàèìåíîâàíèå | Êîë. | Ïðèìå- ÷àíèå |
||||||
| Ñòàíäàðòíûå èçäåëèÿ | |||||||||
| Ïîäøèïíèêè: | |||||||||
| 19 | Ðîëèêîâûé êîíè÷åñêèé | 2 | |||||||
| 7205 ÃÎÑÒ 333-79 | |||||||||
| 20 | Øàðèêîâûé ðàäèàëüíî-óïîðíûé | 2 | |||||||
| 46303 ÃÎÑÒ 831-75 | |||||||||
| Êðåïåæíûå èçäåëèÿ: | |||||||||
| 21 | Âèíò Ì8õ25.36 ÃÎÑÒ 11738-84 | 16 | |||||||
| 22 | Âèíò Ì5õ30.36 ÃÎÑÒ 1491-80 | 4 | |||||||
| 23 | Áîëò Ì10õ90.36 ÃÎÑÒ 7798-70 | 4 | |||||||
| 24 | Áîëò Ì10õ40.36 ÃÎÑÒ 7798-70 | 4 | |||||||
| 25 | Ãàéêà Ì12.4 ÃÎÑÒ 5915-70 | 8 | |||||||
| 26 | Øàéáà 8 65Ã ÃÎÑÒ 6402-70 | 16 | |||||||
| 27 | Øàéáà 10 65Ã ÃÎÑÒ 6402-70 | 8 | |||||||
| 28 | Øòèôò 5õ30 ÃÎÑÒ 3129-70 | 2 | |||||||
| 29 | Ìàíæåòà 32õ52 ÃÎÑÒ 8752-79 | 1 | |||||||
| 30 | Ìàíæåòà 28õ47 ÃÎÑÒ 8752-79 | 1 | |||||||
| 31 | Øïîíêà 10õ8 ÃÎÑÒ 23360-78 | 1 | |||||||
| Ìàòåðèàëû : | |||||||||
| 32 | Ìàñëî ÒÀÄ-17èÃÎÑÒ 23652-79 | 0,7ë | |||||||
| ÊÍÓ.ÕÒ.000 ÑÏ | Ëèñò | ||||||||
| 2 | |||||||||
| Èçì | . Ëèñò | ¹ äîêóìåíòà | Ïîäïèñü | Äàòà | |||||
Ëèòåðàòóðà 1. Àðêóøà À.È. Òåõíè÷åñêàÿ ìåõàíèêà. Òåîðåòè÷åñêàÿ ìåõàíèêà è ñîïðîòèâëåíèå ìàòåðèàëîâ. Ì., «Âûñøàÿ øêîëà», 1989. 2. Àðòîáîëåâñêèé È.È. Òåîðèÿ ìàøèí è ìåõàíèçìîâ. Ì., «Íàóêà», 1975. 3. Áàáóëèí Í.À. Ïîñòðîåíèå è ÷òåíèå ìàøèíîñòðîèòåëüíûõ ÷åðòåæåé. Ì.: «Âûñøàÿ øêîëà», 1987. 4. Äåòàëè ìàøèí, àòëàñ êîíñòðóêöèé / Ïîä ðåä. Ðåøåòîâà Ä.Í. Ì.: Ìàøèíîñòðîåíèå, 1979 5. Äóíàåâ Ï.Ô., Ëåëèêîâ Î.Ï. Äåòàëè ìàøèí. Êóðñîâîå ïðîåêòèðîâàíèå. Ì.: «Âûñøàÿ øêîëà», 1990. 6. Èöêîâè÷ Ã.Ì., Êèñåëåâ Â.À. è äð. Êóðñîâîå ïðîåêòèðîâàíèå äåòàëåé ìàøèí. Ì., «Ìàøèíîñòðîåíèå», 1965. 7. Êóêëèí Í.Ã., Êóêëèíà Ã.Ñ. Äåòàëè ìàøèí. Ì., «Ìàøèíîñòðîåíèå», 1987. 8. Ìåòîäè÷åñêèå óêàçàíèÿ è âàðèàíòû ê çàäàíèÿì äëÿ ñòóäåíòîâ íåìåõàíè÷åñêèõ ñïåöèàëüíîñòåé. Áèøêåê, «Êûðãûçñêèé Òåõíè÷åñêèé Óíèâåðñèòåò»; ñîñò. Ïàíîâà Ë.Ò., Öîé Ó.À., 1996. 9. Ìåòîäè÷åñêèé óêàçàíèÿ ê âûïîëíåíèþ êóðñîâîãî ïðîåêòèðîâàíèÿ äëÿ ñòóäåíòîâ íåìåõàíè÷åñêèõ ñïåöèàëüíîñòåé. Ôðóíçå, «Ôðóíçåíñêèé Ïîëèòåõíè÷åñêèé Èíñòèòóò»; ñîñò. Ôðåéç Â.Í., Óñóáàëèåâ Æ.Ó. 10.×åðíàâñêèé Ñ.À., Èöêîâè÷ Ã.Ì. è äð. Êóðñîâîå ïðîåêòèðîâàíèå äåòàëåé ìàøèí. Ì., «Ìàøèíîñòðîåíèå», 1979. 11.×åðíàâñêèé Ñ.À., Ñíåñàðåâ Ã.À. Ïðîåêòèðîâàíèå ìåõàíè÷åñêèõ ïåðåäà÷. Ì., «Ìàøèíîñòðîåíèå», 1984. 12.Øåéíáëèò À.Å. Êóðñîâîå ïðîåêòèðîâàíèå äåòàëåé ìàøèí. Ì., «Âûñøàÿ øêîëà», 1991. |
|||||||||||||
| ÊÍÓ.ÕÒ.000 ÑÏ | Ëèñò | ||||||||||||
| 37 | |||||||||||||
| Èçì. | Ëèñò | ¹ äîêóìåíòà | Ïîäïèñü | Äàòà | |||||||||
Ñîäåðæàíèå Çàäàíèå……………………………………………………………………………………………………………………………………………………………………………2 1. Ñòðóêòóðíûé àíàëèç ìåõàíèçìà…………………………………………………………………………………………………………………………..3 2. Êèíåìàòè÷åñêèé àíàëèç ìåõàíèçìà ïîäàò÷èêà õëåáîðåçàòåëüíîé ìàøèíû ÌÐÕ – 200………5 3. Äèíàìè÷åñêèé àíàëèç ìåõàíèçìà………………………………………………………………………………………………………………………….8 4. Êèíåìàòè÷åñêèé ðàñ÷åò ïðèâîäà……………………………………………………………………………………………………………………...…13 5. Ðàñ÷åò ÷åðâÿ÷íîé ïåðåäà÷è…………………………………………………………………………………………………………………………….........15 6. Ïðîåêòíûé ðàñ÷åò âàëîâ ðåäóêòîðà è ïîäøèïíèêîâ………………………………………………………………………...……..23 7. Êîíñòðóêòèâíûå ðàçìåðû ÷åðâÿêà è ÷åðâÿ÷íîãî êîëåñà………………………………………………………………………..25 8. Ðàñ÷åò ýëåìåíòîâ êîðïóñà ðåäóêòîðà…………………………………………………………………………………………………………….26 9. Ïðîâåðêà äîëãîâå÷íîñòè ïîäøèïíèêîâ…………………………………………………………………………………………………………..…27 10. Ïðîâåðêà ïðî÷íîñòè øïîíî÷íîãî ñîåäèíåíèÿ è ïîñàäêè âåíöà ÷åðâÿ÷íîãî êîëåñà………………...30 11. Âûáîð ñìàçêè è óïëîòíèòåëüíûõ óñòðîéñòâ………………………………………………………………………………………………..32 12. Ñáîðêà ðåäóêòîðà………………………………………………………………………………………………………………………………………………………...33 Ïðèëîæåíèå………………………………………………………………………………………………………………………………………………………………..34 Ëèòåðàòóðà………………………………………………………………………………………………………………………………………………………………37 |
|||||||||||||
| ÊÍÓ.ÕÒ.000 ÏÇ | Ëèñò | ||||||||||||
| 38 | |||||||||||||
| Èçì. | Ëèñò | ¹ äîêóì. | Ïîäïèñü | Äàòà | |||||||||
Похожие работы
-
Расчет водопроводной сети
Расчет магистрального трубопровода . Определение высоты водонапорной башни . Определение расходов. Курсовая работа Еронько Ирины 3016/I группы МВ и ССО РФ
-
Законы распределения случайных процессов
Государственный комитет Российской Федерации по высшему образованию МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ОТКРЫТЫЙ УНИВЕРСИТЕТ Кафедра электронной техники
-
Процессное управление издержками на предприятиях станкостроительной промышленности
Целью работы является комплексное теоретическое исследование перспектив внедрения принципов процессного управления издержками на предприятиях станкостроительного комплекса и их преимуществ по сравнению с традиционными методами оптимизации.
-
Электронные, квантовые приборы и микроэлектроника
Программа, методическое указание и контрольные задания (для студентов заочной формы обучения специальности 3805 – Радиосвязь, радиовещание и телевидение).
-
Ракетный двигатель РД-583 РН Зенит-3
Государственное образовательное учреждение профессионального образования Ижевский Государственный технический университет Кафедра "Тепловые двигатели и установки"
-
Автоматизация методической печи
Конструкция методической печи и технологический процесс ее нагревания. Разработка структурной, функциональной, принципиальной схем автоматизации работы агрегата. Математическая модель нагрева металла в печи на основании метода конечных разностей.
-
Механизм подъема и его расчет
Расчет механизма подъема: определение массы подвижных частей, расчет и подбор каната, канатоведущего шкива, натяжения канатов подвески, электродвигателя, редуктора лебедки, тормоза, каната, барабана. Расчетное обоснование геометрических характеристик.
-
Железобетонные конструкции
Разработать проект межэтажного перекрытия 4-х этажного промышленного здания.Наружные стены здания выполнены в кирпиче толщиной 510 мм. Перекрытия , колонны , фундамент изготовляются в монолитном железобетоне.
-
Отчет по учебно - ознакомительной практике
Ростокинский з-д ЖБК. Краткая схема и технология производства. Бетоносмесительный цех. Краснопресненский завод ЖБК. Технология изготовления. Вопросы охраны труда.
-
Разработать технологическую схему производства стали марки 35Г2 и определить основные техникоэкономические показатели производства
Разработкаь технологической схемы производства стали марки 35Г2. Характеристика марки стали 35Г2. Анализ состава чугуна, внедоменная обработка чугуна. Определение максимально воможной доли лома. Продувка. Внепечная обработка. Разливка.
 1
Â
1
   Â
  
 C B
C B  aB
=aB
n
= ω2
AB
•lAB
=222
•0,05 =24,2ì/ñ2
aB
=aB
n
= ω2
AB
•lAB
=222
•0,05 =24,2ì/ñ2
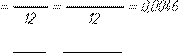 m
m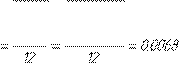 m
m R
R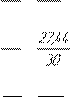 G
G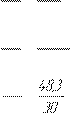 F
F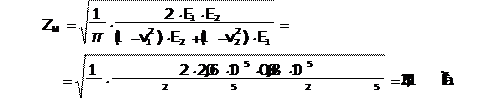 π
(1 −0,35 )⋅0,88⋅10 +(1 −0,49)⋅2,06⋅10
π
(1 −0,35 )⋅0,88⋅10 +(1 −0,49)⋅2,06⋅10 Zε
= = =0,848, ãäå
Zε
= = =0,848, ãäå 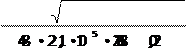 f =1197, 3 • (377,57)2 + 485( 75, )2 =0,0047ìì
f =1197, 3 • (377,57)2 + 485( 75, )2 =0,0047ìì