Название: Расчётно-графическое задание

Вид работы: реферат

Рубрика: Информатика

Размер файла: 168.89 Kb

Скачать файл: referat.me-130713.docx

Краткое описание работы: Цель и назначение работы Целью выполнения расчетно-графической работы является закрепление знаний, умения и навыков, необходимых для математического моделирования социально-экономических процессов. А также, приобретение навыков работы с программными пакетами.

Расчётно-графическое задание

Цель и назначение работы

Целью выполнения расчетно-графической работы является закрепление знаний, умения и навыков, необходимых для математического моделирования социально-экономических процессов. А также, приобретение навыков работы с программными пакетами.

Задание на выполнение РГР

Задание №1

На фабрике с помощью 5 видов красителей (А1-А5) создается 4 разновидности рисунков для тканей (Р1-Р4). При известной отпускной стоимости 1 м ткани каждого рисунка (руб.), известном расходе каждого красителя на окраску 1 м ткани (г) и известном запасе каждого красителя (кг):

2.1.1 определить план выпуска ткани каждого рисунка, обеспечивающий максимальную прибыль от реализации тканей;

2.1.2 составить двойственную задачу и найти ее решение;

2.1.3 определить теневые цены на каждый краситель; указать дефицитные и недефицитные красители;

2.1.4. указать на сколько недоиспользуются недефицитные красители;

2.1.5 показать прибыль, план выпуска тканей каждого рисунка и недоиспользование недефицитных красителей при увеличении запасов дефицитных красителей на 1 ед.;

2.1.6 показать допустимые пределы изменения запасов красителей;

2.1.7 показать допустимые пределы изменения цен на выпускаемые виды тканей.

2.1.8 оценить целесообразность введения в план производства выпуск ткани с разновидностью рисунка Р5, если нормы затрат красителей на 1 единицу ткани соответственно равны: 6; 2; 1; 4; 4; и доход, ожидаемый от реализации новой ткани равен 5000 руб;

2.1.9 показать, допустимо ли увеличение всех дефицитных красителей одновременно на 10 кг.

Номер варианта	Вид красителей	Разновидность рисунка. Расход красителей на окраску 1 м ткани (г).				Запасы красителей (кг).
		Р1	Р2	Р3	Р4
8	А1	7	6	5	21	500
	А2	9	13	17	16	1402
	А3	5	7	15	19	203
	А4	17	5	24	23	600
	А5	4	7	9	2	150
	Стоимость одного метра ткани (руб.)	124	125	195	274

Составляем экономико – математическую модель задачи.

Обозначим:

Х₁ – план выпуска продукции вида Р₁ ;

Х₂ – план выпуска продукции вида Р₂ ;

Х₃ – план выпуска продукции вида Р₃ ;

Х₄ – план выпуска продукции вида Р₄ .

Приведем задачу к каноническому виду:

Решаем задачу с помощью симплекс –таблицы.

Таблица 1

Базис	Сб	Опорное решение	С1	С2	С3	С4	С5	С6	С7	С8	С9
			124	125	195	274	0	0	0	0	0
			А1	А2	А3	А4	А5	А6	А7	А8	А9
А5	0	500	7	6	5	21	1	0	0	0	0
А6	0	1402	9	13	17	16	0	1	0	0	0
А7	0	203	5	7	15	19	0	0	1	0	0
А8	0	600	17	5	24	23	0	0	0	1	0
А9	0	150	4	7	9	2	0	0	0	0	1
∆j	F=0		-124	-125	-195	-274	0	0	0	0	0

Таблица 2

Базис	Сб	Опорное решение	С1	С2	С3	С4	С5	С6	С7	С8	С9
			124	125	195	274	0	0	0	0	0
			А1	А2	А3	А4	А5	А6	А7	А8	А9
А5	0	275,6	1,5	-1,7	-11,6	0	1	0	-1,1	0	0
А6	0	1231,1	4,8	7,1	4,4	0	0	1	-0,8	0	0
А4	274	10,7	0,3	0,4	0,8	1	0	0	0,05	0	0
А8	0	354,3	10,9	-3,4	5,8	0	0	0	-1,2	1	0
А9	0	128,6	3,4	6,2	7,4	0	0	0	-0,1	0	1
∆j	F=2927,47		-51,9	-24,1	21,3	0	0	0	14,4	0	0

Таблица 3

Базис	Сб	Опорное решение	С1	С2	С3	С4	С5	С6	С7	С8	С9
			124	125	195	274	0	0	0	0	0
			А1	А2	А3	А4	А5	А6	А7	А8	А9
А5	0	227,9	0	-1,3	-12,4	0	1	0	-0,9	-0,1	0
А6	0	1076,1	0	8,6	1,8	0	0	1	-0,3	-0,4	0
А4	274	2,2	0	0,5	0,6	1	0	0	0,08	-0,02	0
А1	124	32,4	1	-0,3	0,5	0	0	0	-0,11	0,09	0
А9	0	16,2	0	7,4	5,6	0	0	0	0,28	-0,03	1
∆j	F=4606,81		0	-40,5	49	0	0	0	8,7	4,7	0

Таблица 4

Базис	Сб	Опорное решение	С1	С2	С3	С4	С5	С6	С7	С8	С9
			124	125	195	274	0	0	0	0	0
			А1	А2	А3	А4	А5	А6	А7	А8	А9
А5	0	230,7	0	0	-11,4	0	1	0	-0,89	-0,19	0,17
А6	0	1057,07	0	0	-4,71	0	0	1	-0,64	-0,07	-1,17
А4	274	1,173	0	0	0,307	1	0	0	0,065	-0,005	-0,061
А1	124	33,06	1	0	0,77	0	0	0	-0,1	0,08	0,04
А2	125	2,2	0	1	0,76	0	0	0	0,038	-0,04	0,14
∆j	F=4696,05		0	0	79,64	0	0	0	10,22	2,99	5,5

Отрицательных оценок в оценочной строке нет; решение оптимально. Оптимальный опорный план:

Х_опт =(33,06; 2,2; 0; 1,173; 0; 0; 0; 0; 0)^Т

F_max =4696,05 руб.

Для получения максимальной прибыли 4696,05 руб. необходимо выпустить продукции вида Р1 33,06 м ткани, Р2 2,2 м и Р4 1,173 м.

Продукция видов Р₃ является убыточным; его производство является нерентабельным.

составим двойственную задачу.

- теневая цена ресурса I

- теневая цена ресурса II

- теневая цена ресурса Ш

- теневая цена ресурса IV

- теневая цена ресурса V

→min

≥

Т.к. в прямой задаче все неравенства в системе сильных ограничений вида “≤”, найдем решение двойственной задачи по результатам решения прямой задачи.

=4696,05 руб.

y₁ =0

y₂ =0

y₃ =10,22

y₄ =2,99

y₅ =5,5

Дефицитным являются ресурсы III, IVи V.

Недефицитными являются ресурсы I, II.

Недефицитные ресурсы недоиспользуются:

I ресурс на 230,7 кг;

II ресурс на 1057,07 кг

При увеличении запаса III ресурса на 1 ед. (204 кг) можно получить увеличение прибыли на 10,22 руб. она составит F=4706,27 руб. При этом план выпуска продукции 4 надо увеличить на 0,065 т.е. x₄ =1,238, продукции 1 надо увеличить на -0,1 т.е. x₁ =2,1, продукции 2 надо увеличить на 0,038 т.е. x₂ =33,098. В этом случае недефицитные ресурсы будут недоиспользоваться:

1 ресурс на 0,89; его недоиспользование составит 231,69 кг;

2 ресурс на 0,64; его недоиспользование составит 1057,71 кг

Покажем допустимые пределы изменения запасов ресурсов.

Составим матрицу Р

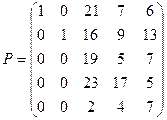
и вектор столбец

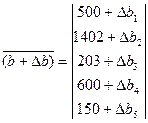
Найдем матрицу P

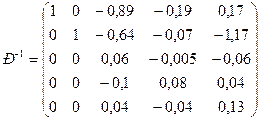
Р^-1 (b+∆b)= =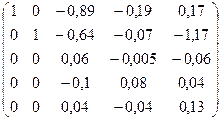

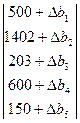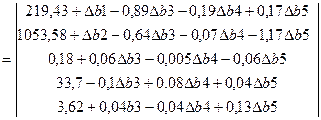
Покажем допустимые пределы изменения цен на выпускаемые виды продукции.

p^-1 (c+∆c)

Для выполнения данного пункта необходимо решить двойственную задачу симплекс-методом.

Приводим задачу к каноническому виду

F*= - 500y₁ -1402y₂ -203y₃ -600y₄ -150y₅ +0y₆ +0y₇ +0y₈ +0y₉ →max

7y₁ +9y₂ +5y₃ +17y₄ +4y₅ -y₆ =124

6y₁ +13y₂ +7y₃ +5y₄ +7y₅ -y₇ =125

5y₁ +17y₂ +15y₃ +24y₄ +23y₅ -y₈ =195

21y₁ +16y₂ +19y₃ +23y₄ +2y₅ -y₉ =274

i=

Т.к. начальный базис указать невозможно, то решаем задачу методом искусственных переменных.

G=0y₁ +0y₂ +0y₃ +0y₄ +0y₅ +0y₆ +0y₇ +0y₈ +0y₉ -y₁₀ -y₁₁ -y₁₂ -y₁₃ →min

7y₁ +9y₂ +5y₃ +17y₄ +4y₅ -y₆ +y₁₀ =124

6y₁ +13y₂ +7y₃ +5y₄ +7y₅ -y₇ +y₁₁ =125

5y₁ +17y₂ +15y₃ +24y₄ +9y₅ -y₈ +y₁₂ =195

21y₁ +16y₂ +19y₃ +23y₄ +2y₅ -y₉ +y₁₃ =274

i=

Базис	Сб	Опорное решение	С1	С2	С3	С4	С5	С6	С7	С8	С9
			500	1402	203	600	150	0	0	0	0
			А1	А2	А3	А4	А5	А6	А7	А8	А9
А4	-600	2,99	0,19	0,07	0	1	0	-0,08	0,04	0	0,005
А5	-150	5,5	-0,17	1,17	0	0	1	-0,04	-0,13	0	-0,06
А3	-203	10,2	0,9	0,6	1	0	0	0,01	-0,04	0	-0,06
А8	0	79,6	11,4	4,7	0	0	0	-0,8	-0,76	1	-0,3
∆j	F=-4696,05		230,07	1057	0	0	0	33,6	2,2	0	1,17

Заключительная симплекс-таблиц

Составим матрицу P и вектор-столбец

P = ;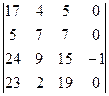

=

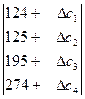
Найдём матрицу

=

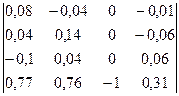
∆ c)= *=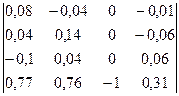

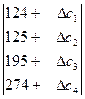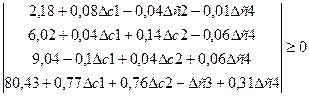
Покажем целесообразность введения в план производства выпуск ткани с разновидностью рисунка Р5:

∆p₅ =6*0+2*0+1*10,22+4*2,99+4*5,5-5000=-4955,82

Т.к. ∆р₅ <0, то есть смысл ввести в план производства выпуск ткани с разновидностью рисунка р₅ .

Определяем, допустимо ли одновременное увеличение запасов дефицитных красителей на 10 кг каждого. Пределы изменения запасов красителей определяются из условия

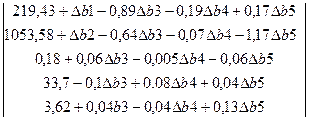
Дефицитным является краситель А₃ , А₄ и А₅ . Значит Db₃ =10, Db₄ =10 и Db₅ =10. Остальные Db₁ =Db₂ =0, тогда

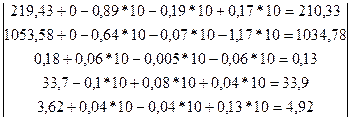
Увеличение дефицитных красителей не приводит к изменению плана производства тканей.

Задание №2

Коммивояжер выезжает из одного из городов (все равно какого) и должен объехать все города, преодолев минимальное расстояние. При этом в каждый город он может только 1 раз въехать и только 1 раз выехать. Составить экономико-математическую модель задачи и решить задачу методом ветвей и границ.

Дон.	Ерев.	Жит.	Казань	Калин.	Каун.
Донецк	1523	863	1899	1809	1578
Ереван	1523	2329	1622	3275	3044
Житомир	863	2329	1801	1208	977
Казань	1899	1622	1801	2023	1792
Калининград	1809	3275	1208	2023	247
Каунас	1578	3044	977	1792	247

F = 1523x ₁₂ + 1523₂₁ + 863x ₁₃ + 863x ₃₁ + 1899x ₁₄ + 1899x ₄₁ + 1809x ₁₅ + 1809x ₅₁ + 1578x ₁₆ + 1578x ₆₁ + 2329x ₃₂ + 2329x ₂₃ + 1622x ₂₄ +1622x ₄₂ + 3275x ₂₅ + 3275x ₅₂ + 3044x ₂₆ + 3044x ₆₂ + 1801x ₃₄ + 1801x ₄₃ + 1208x ₃₅ + 1208x ₅₃ + 977x ₃₆ + 977x ₆₃ + 2023x ₄₅ + 2023x ₅₄ + 1792x ₄₆ + 1792x ₆₄ + 247x ₅₆ + 247x ₆₅ min

x ₁₂ + x ₁₃ + x ₁₄ + x ₁₅ + x ₁₆ = 1

x ₂₁ + x ₂₃ + x ₂₄ + x ₂₅ + x ₂₆ = 1

x ₃₁ + x ₃₂ + x ₃₄ + x ₃₅ + x ₃₆ = 1

x ₄₁ + x ₄₂ + x ₄₃ + x ₄₅ + x ₄₆ = 1

x ₅₁ + x ₅₂ + x ₅₃ + x ₅₄ + x ₅₆ = 1

x ₆₁ + x ₆₂ + x ₆₃ + x ₆₄ + x ₆₅ = 1

x ₂₁ + x ₃₁ + x ₄₁ + x ₅₁ + x ₆₁ = 1

x ₁₂ + x ₃₂ + x ₄₂ + x ₅₂ + x ₆₂ = 1

x ₁₃ + x ₂₃ + x ₄₃ + x ₅₃ + x ₆₃ = 1

x ₁₄ + x ₂₄ + x ₃₄ + x ₅₄ + x ₆₄ = 1

x ₁₅ + x ₂₅ + x ₃₅ + x ₄₅ + x ₆₅ = 1

x ₁₆ + x ₂₆ + x ₃₆ + x ₄₆ + x ₅₆ = 1

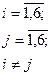
Решение задачи методом ветвей и границ.

Преобразуем матрицу s

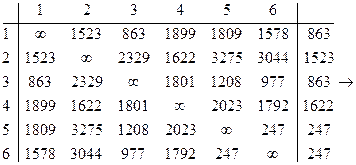
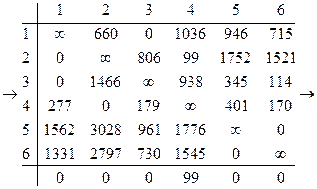
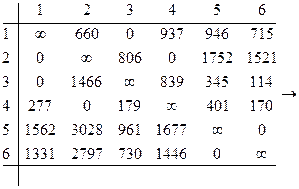
Определяем сумму приводимых элементов

h¹ =863+1523+863+1622+247+247+99=5464

Определяем претендентов для ветвления в множестве Y

Претендентами на ветвление могут быть S₁₃ , S₂₁ , S₂₄ , S₃₁ , S₄₂ , S₅₆ ,S₆₅

Q₁₃ = 660+179=839;

Q₂₁ = 0;

Q₂₄ = 839;

Q₃₁ = 114;

Q₄₂ =660+170=830;

Q₅₆ = 170+961=1131;

Q₆₅ = 345+730=1075

Максимальную оценку имеет маршрут: Q42=830

w = h¹ +Q42= 5464 + 830 = 6294

Преобразуем матрицу:

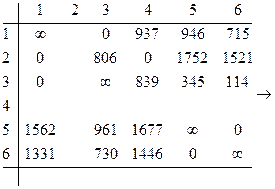
Определяем h² = 0;

Оценка по {4,2}=5464

Определяем пару для ветвления

Q₁₃ = 715+730=1445;

Q₂₁ = 0;

Q₂₄ = 839;

Q₃₁ = 114;

Q₅₆ = 114+961=1075;

Q₆₅ = 345+730=1075

Подходящую оценку имеет маршрут: Q21=0

w = w(4;2)+ Q21= 6294

Преобразуем матрицу:

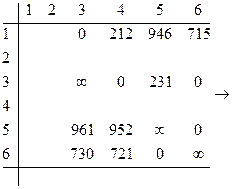
Определяем h³ = 114+725=839;

Оценка по {2,1}=5464+839=6303

Определяем пару для ветвления

Q₁₃ = 212+730=942;

Q₃₄ = 212;

Q₃₆ = 0;

Q₅₆ = 952;

Q₆₅ = 231+721=952

Подходящую оценку имеет маршрут: Q13=942

w = w(2;1)+ Q13= 6294+942=7236

Преобразуем матрицу:

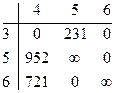
Определяем h⁴ = 0;

Оценка по {1,3}= 6303

Определяем пару для ветвления

Q₃₄ = 721;

Q₃₆ = 0;

Q₅₆ = 952;

Q₆₅ = 231

Подходящую оценку имеет маршрут: Q36=0

w = w(1;3)+ Q36= 7236

Преобразуем матрицу:

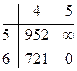
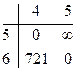Матрица приведена

Определяем h⁵ =952;

Оценка w{3,6}=6303+721=7024

5464 6303 6303 7024

G₀ 4,2 2,1 1,3 3,6

6294 6294 7236 7236

4,2 2,1 1,3 3,6

Нужный маршрут Казань – Ереван – Донецк – Житомир – Каунас – Калининград.

Т.к. оценка последнего маршрута больше оценки одного из тупиковых ветвей, а именно , то необходимо доисследовать процесс ветвления этой ветви.

Возвращаемся к исходной матрице расстояний и полагаем в ней

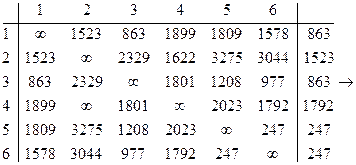
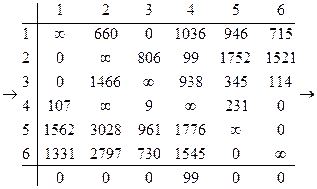
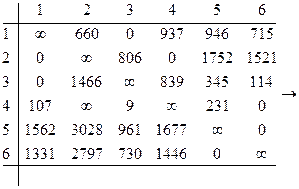
Определяем сумму приводимых элементов

h⁶ =5634

Определяем претендентов для ветвления в множестве Y

Претендентами на ветвление могут быть S₁₃ , S₂₁ , S₂₄ , S₃₁ , S₄₆ , S₅₆ ,S₆₅

Q₁₃ = 660+9=669;

Q₂₁ = 0;

Q₂₄ = 839;

Q₃₁ = 114;

Q₄₆ =9;

Q₅₆ = 961;

Q₆₅ = 231+730=961

Максимальную оценку имеет маршрут: Q56=961

w = h⁶ +Q56= 5634 + 961 = 6595

Преобразуем матрицу:

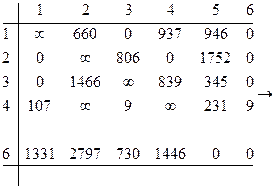
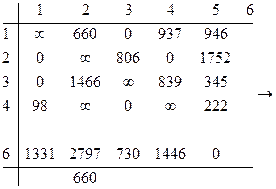
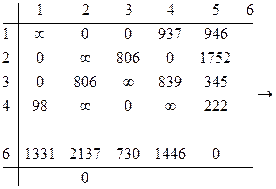
Определяем h⁷ = 669;

Оценка по {5,6}=5634+669=6303

Определяем пару для ветвления

Q₁₂ = 806;

Q₁₃ = 0;

Q₂₁ = 0;

Q₂₄ = 839;

Q₃₁ = 345;

Q₄₃ = 98;

Q₆₅ = 730+345=1075

Подходящую оценку имеет маршрут: Q24=839

w = w(5;6)+ Q24= 6595+839=7434

Преобразуем матрицу:

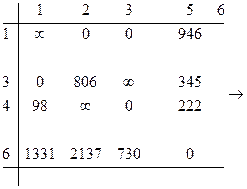
Определяем h⁸ = 0;

Оценка по {2,4}=6303

Определяем пару для ветвления

Q₁₂ = 806;

Q₁₃ = 0;

Q₃₁ = 98+345=443;

Q₄₃ = 98;

Q₆₅ = 730+222=952

Подходящую оценку имеет маршрут: Q12=806

w = w(2;4)+ Q12= 7434+806=8240

Преобразуем матрицу:

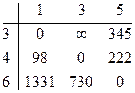
Определяем h⁹ = 0;

Оценка по {1,2}= 6303

Определяем пару для ветвления

Q₃₁ = 98+345=443;

Q₄₃ = 730+98=828;

Q₆₅ = 730+222=952

Подходящую оценку имеет маршрут: Q43=828

w = w(4;3)+ Q12= 8240+828=9068

Преобразуем матрицу:

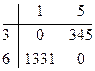Матрица приведена

Определяем h¹⁰ =0;

Оценка w{4,3}=6303

Т.к. получена матрица 2x2 и оценка последнего маршрута не больше всех тупиковых ветвей, то решение оптимально. Маршрутами для завершения могут быть пары (3,1), (6,5).

Составим геометрическую интерпретацию найденного маршрута

5634 5634 6303 6303 6303 6303

G₀ 5,6 2,4 1,2 4,3 3,1

6,5

6595 7434 8240 9068

10744

5,6 2,4 1,2 4,3 3,1 10744

6,5

Нужный маршрут Казань – Ереван – Донецк – Житомир – Каунас – Калининград; x₄₂ =1, x₂₁ =1, x₁₃ =1, x₃₆ =1, x₆₅ =1, F=5232 км.

Задание №3

На предприятии необходимо выполнить последовательно 12 видов работ (R1÷R12). 12 сотрудников предприятия (S1÷S12) затрачивают на выполнение каждого вида работ различное время в часах. Распределить работников по видам работ так, чтобы общее время на выполнение работ было минимально. Очередность выполнения работ не имеет значения.

Составить экономико-математическую модель задачи и решить задачу с помощью венгерского алгоритма.

№ варианта	Сотрудник	Виды работ Время, затрачиваемое каждым сотрудником на выполнение каждого вида работ
		R1	R2	R3	R4	R5	R6	R7	R8	R9	R10	R11	R12
8	S1	10	2	3	7	7	9	10	10	10,5	12	14,5	7
	S2	12	1	5	6,5	7,5	10	8	9	10	11	14	7,5
	S3	11	1	3,5	6,5	8	10,5	8	9	12	11	15	7,5
	S4	11	2	4	6,5	8	11	8	9,5	12	12	15,5	7,5
	S5	10	2,5	4	5	8	11,5	8,5	8	11	12	15,5	6
	S6	10	2,5	4,5	5	7,5	10,5	8,5	8	11	12	15	6
	S7	9,5	1	4	5,5	7,5	10,5	8,5	9	11	12	15,5	6
	S8	9,5	1	3,5	6,5	7	10,5	10	10,5	12	10	15,5	6
	S9	9,8	3	3,5	6,5	7	11	10,5	10	12	10	15	7
	S10	8	3	3	6,5	7	11	10,5	10	9,5	12	15	6,5
	S11	8	3	3	6,5	7,5	10	11	10,5	9,5	12	15,5	6,5
	S12	8	3	3	6,5	7,5	9	11	10,5	9,5	12	15	6,5

Составляем экономико-математическую модель задачи

F = 10x ₁₁ + 2x ₁₂ + 3x ₁₃ + 7x ₁₄ + 7x ₁₅ + 9x ₁₆ + 10x ₁₇ + 10x ₁₈ + 10,5x ₁₉ + 12x ₁₁₀ + 14,5x ₁₁₁ + 7x ₁₁₂ + 12x ₂₁ + x ₂₂ + 5x ₂₃ + 6,5x ₂₄ + 8x ₂₅ + 10,5x ₂₆ + 8x ₂₇ + 9x ₂₈ + 12x ₂₉ + 11x ₂₁₀ + 15x ₂₁₁ + 7,5x ₂₁₂ + 11x ₃₁ + x ₃₂ + 3,5x ₃₃ + 6,5x ₃₄ + 8x _3,5 + 10,5x ₃₆ + 8x ₃₇ + 9x ₃₈ + 12x ₃₉ + 11x ₃₁₀ + 15x ₃₁₁ +17,5x ₃₁₂ + 11x ₄₁ + 2x ₄₂ + 4x ₄₃ + 6,5x ₄₄ + 8x ₄₅ + 11x ₄₆ + 8x ₄₇ + 9,5x ₄₈ + 12x ₄₉ + 12x ₄₁₀ + 15,5x ₄₁₁ + 7,5x ₄₁₂ + 10x ₅₁ + 2,5x ₅₂ + 4x ₅₃ + 5x ₅₄ + 8x ₅₅ + 11,5x ₅₆ + 8,5x ₅₇ + 8x ₅₈ + 11x ₅₉ + 12x ₅₁₀ + 15,5x ₅₁₁ + 6x ₅₁₂ + 10x ₆₁ + 2,5x ₆₂ + 4,5x ₆₃ + 5x ₆₄ + 7,5x ₆₅ + 10,5x ₆₆ + 8,5x ₆₇ + 8x ₆₈ + 11x ₆₉ + 12x ₆₁₀ + 15x ₆₁₁ + 6x ₆₁₂ + 9,5x ₇₁ + x ₇₂ + 4x ₇₃ + 5,5x ₇₄ + 7,5x ₇₅ + 10,5x ₇₆ +8,5x ₇₇ + 9x ₇₈ + 11x ₇₉ + 12x ₇₁₀ + 15,5x ₇₁₁ + 6x ₇₁₂ + 9,5x ₈₁ + 1x ₈₂ + 3,5x ₈₃ + 6,5x ₈₄ + 7x ₈₅ + 10,5x ₈₆ + 10x ₈₇ + 10,5x ₈₈ + 12x ₈₉ + 10x ₈₁₀ + 15,5x ₈₁₁ + 6x ₈₁₂ + 9,5x ₉₁ + 3x ₉₂ + 3x ₉₃ + 3,5x ₉₄ + 6,5x ₉₅ + 7x ₉₆ + 11x ₉₇ + 10,5x ₉₈ + 10x ₉₉ +12x ₉₁₀ +15x ₉₁₁ + 7x ₉₁₂ + 8x ₁₀₁ + 3x ₁₀₂ + 3x ₁₀₃ + 6,5x ₁₀₄ + 7x ₁₀₅ + 11x ₁₀₆ + 10,5x ₁₀₇ + 10x ₁₀₈ + 9,5x ₁₀₉ + 12x ₁₀₁₀ + 15,5x ₁₀₁₁ + 6,5x ₁₀₁₂ + 8x ₁₁₁ + 3x ₁₁₂ + 3x ₁₁₃ + 6,5x ₁₁₄ + 7,5x ₁₁₅ + 10x ₁₁₆ + 11x ₁₁₇ + 10,5x ₁₁₈ + 9,5x ₁₁₉ + 12x ₁₁₁₀ + 15,5x ₁₁₁₁ + 6,5x ₁₁₁₂ + 8x ₁₂₁ + 3x ₁₂₂ + 3x ₁₂₃ + 6,5x ₁₂₄ + 7,5x ₁₂₅ + 9x ₁₂₆ + 11x ₁₂₇ + 10,5x ₁₂₈ + 9,5x ₁₂₉ + 12x ₁₂₁₀ + 15x ₁₂₁₁ + 6,5x ₁₂₁₂ min

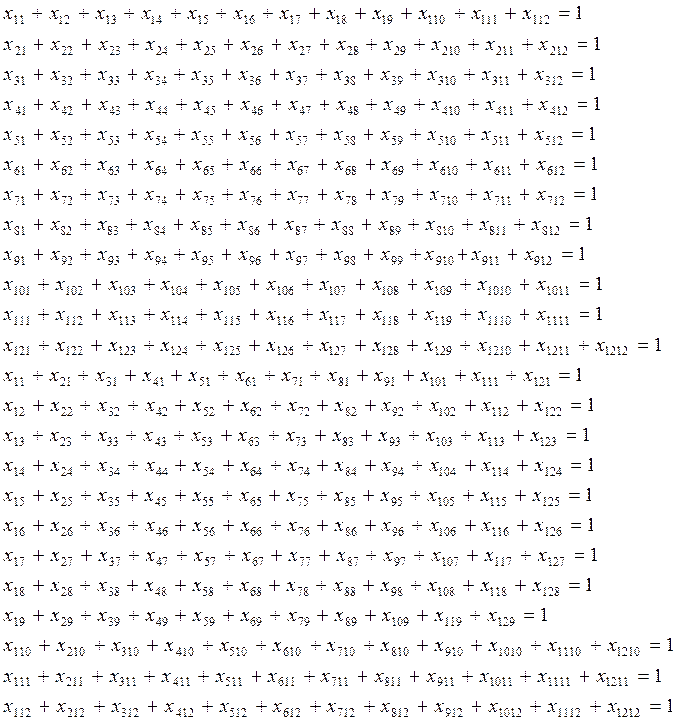
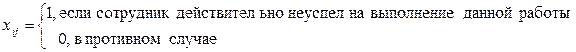
По исходным данным составляем таблицу

R1	R2	R3	R4	R5	R6	R7	R8	R9	R10	R11	R12
S1	10	2	3	7	7	9	10	10	10,5	12	14,5	7
S2	12	1	5	6,5	7,5	10	8	9	10	11	14	7,5
S3	11	1	3,5	6,5	8	10,5	8	9	12	11	15	7,5
S4	11	2	4	6,5	8	11	8	9,5	12	12	15,5	7,5
S5	10	2,5	4	5	8	11,5	8,5	8	11	12	15,5	6
S6	10	2,5	4,5	5	7,5	10,5	8,5	8	11	12	15	6
S7	9,5	1	4	5,5	7,5	10,5	8,5	9	11	12	15,5	6
S8	9,5	1	3,5	6,5	7	10,5	10	10,5	12	10	15,5	6
S9	9,8	3	3,5	6,5	7	11	10,5	10	12	10	15	7
S10	8	3	3	6,5	7	11	10,5	10	9,5	12	15	6,5
S11	8	3	3	6,5	7,5	10	11	10,5	9,5	12	15,5	6,5
S12	8	3	3	6,5	7,5	9	11	10,5	9,5	12	15	6,5

Преобразуем составляемую таблицу

1 2 3 4 5 6 7 8 9 10 11 12

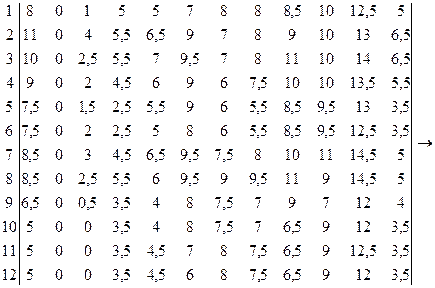
1 2 3 4 5 6 7 8 9 10 11 12

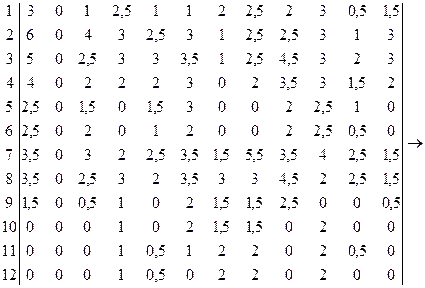
Произведем назначение каждого сотрудника на один из видов работ:

S₁ →R₂ ; S₂ →?; S₃ →?; S₄ →R₇ ; S₅ →R₄ ; S₆ →R₈ ; S₇ →?; S₈ →?; S₉ →R₅ ; S₁₀ →R₁ ; S₁₁ →R₃ ; S₁₂ →R₉

Решение не оптимально; не можем назначить всех сотрудников на выполнение работ.

Делаем дальнейшее преобразование таблицы.

Минимальное число, через которое не проходит ни одна линия: 0,5

1 2 3 4 5 6 7 8 9 10 11 12

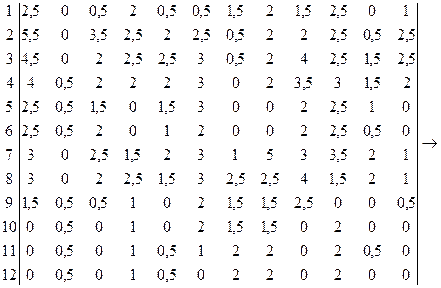
Произведем назначение каждого сотрудника на один из видов работ:

S₁ →R₁₁ ; S₂ →R₂ ; S₃ →?; S₄ →R₇ ; S₅ →R₄ ; S₆ →R₈ ; S₇ →?; S₈ →?; S₉ →R₅ ; S₁₀ →R₁ ; S₁₁ →R₃ ; S₁₂ →R₉

Решение не оптимально; не можем назначить всех сотрудников на выполнение работ.

Делаем дальнейшее преобразование таблицы.

Минимальное число, через которое не проходит ни одна линия: 0,5

1 2 3 4 5 6 7 8 9 10 11 12

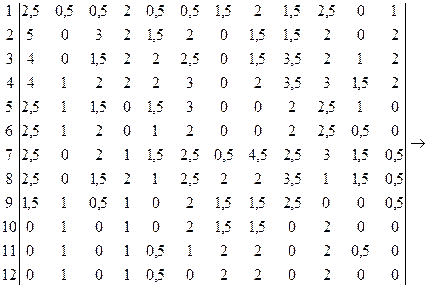
Произведем назначение каждого сотрудника на один из видов работ:

S₁ →R₁₁ ; S₂ →R₂ ; S₃ →?; S₄ →R₇ ; S₅ →R₄ ; S₆ →R₈ ; S₇ →?; S₈ →?; S₉ →R₅ ; S₁₀ →R₁ ; S₁₁ →R₃ ; S₁₂ →R₉

Решение не оптимально; не можем назначить всех сотрудников на выполнение работ.

Делаем дальнейшее преобразование таблицы.

Минимальное число, через которое не проходит ни одна линия: 0,5

1 2 3 4 5 6 7 8 9 10 11 12

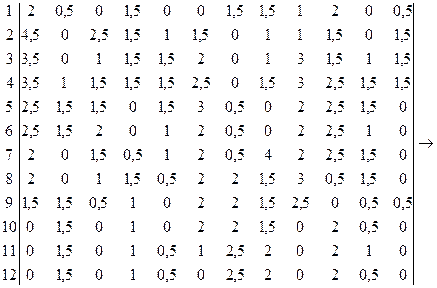
Произведем назначение каждого сотрудника на один из видов работ:

S₁ →R₆ ; S₂ →R₁₁ ; S₃ →R₂ ; S₄ →R₇ ; S₅ →R₄ ; S₆ →R₈ ; S₇ →R₁₂ ; S₈ →?; S₉ →R₁₀ ; S₁₀ →R₅ ; S₁₁ →R₃ ; S₁₂ →R₁

Решение не оптимально; не можем назначить всех сотрудников на выполнение работ.

Делаем дальнейшее преобразование таблицы.

Минимальное число, через которое не проходит ни одна линия: 0,5

1 2 3 4 5 6 7 8 9 10 11 12

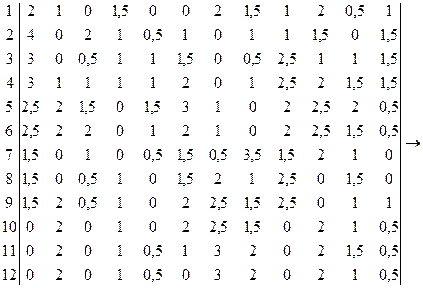
Произведем назначение каждого сотрудника на один из видов работ:

S₁ →R₆ ; S₂ →R₁₁ ; S₃ →R₂ ; S₄ →R₇ ; S₅ →R₄ ; S₆ →R₈ ; S₇ →R₁₂ ; S₈ →R₁₀ ; S₉ →R₅ ; S₁₀ →R₃ ; S₁₁ →R₁ ; S₁₂ →R₉

Решение оптимально; можем назначить всех сотрудников на выполнение работ.

И окончательно:

1 2 3 4 5 6 7 8 9 10 11 12

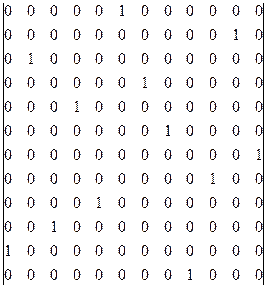
При этом время, затрачиваемое на выполнение всех работ, составит:

88,5 часов.

Альтернативных решений нет, решение единственное.