Машинная имитация случайной последовательности чисел

Федеральное агентство по образованию

Государственное образовательное учреждение высшего

профессионального образования

Тульский государственный университет

Факультет Экономики и Права

Кафедра Автоматизированных информационных и управляющих систем

Отчет по лабораторной работе №1:

« МАШИННАЯ ИМИТАЦИЯ

СЛУЧАЙНЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ ЧИСЕЛ ».

Выполнила: студентка гр.730971

Иммель Я.С.

Принял: Семенчев Е. А.

Тула 2010

ЦЕЛЬ: Изучение функционирования программных датчиков псевдослучайных чисел. Практическая проверка качества генераторов случайных чисел.

Ход работы:

Мультипликативный конгруэнтный метод . Метод представляет собой арифметическую процедуру для генерирования конечной последовательности равномерно распределённых чисел. Основная формула метода имеет вид:

X_i+1 =aX_i (mod m),

где a и m - неотрицательные целые числа. Согласно этому выражению, мы должны взять последнее случайное число X_i , умножить его на постоянный коэффициэнт a и взять модуль полученного числа по m ( т.е. разделить на aX_i и остаток считать как X_i+1 ). Поэтому для генерирования последовательности чисел X_i необходимы начальное значение X₀ , множитель a и модуль m. Эти параметры выбирают так, чтобы обеспечить максимальный период и минимальную корреляцию между генерируемыми числами.

Правильный выбор модуля не зависит от системы счисления, используемой в данной ЭВМ. Для ЭВМ, где применяется двоичная система счисления, m=2^N ( N-число двоичных цифр в машинном слове ). Тогда максимальный период (который получается при правильном выборе a и X₀ )

L=2^N-2 =m/4, (N>2) .

Выбор a и X₀ зависит также от типа ЭВМ. Для двоичной машины

a=8T±3;

где T может быть любым целым положительным числом, а X₀ -любым положительным, но нечётным числом. Указанный выбор констант упрощает и ускоряет вычисления, но не обеспечивает получения периода максимальной длины. Больший период можно получить, если взять m, равное наибольшему простому числу, которое меньше чем 2^N , и a, равное корню из m. Максимальная длина последовательности будет увеличена от m/4 до m-1 ( метод Хатчинсона). Изложенный алгоритм, записанный на псевдокоде, представлен в приложении. Имя подпрограммы-RANDU.

Подпрограмма RANDU (RANDOM) имеется в математическом обеспечении многих ЭВМ (в том числе и РС). При этом константы, используемые в подпрограмме, для 32-разрядного машинного слова имеют значения a=5¹³ =1220703125, i/m=0,4656613E-9.

Смешанные конгруэнтные методы. На основе конгруэнтной формулы были созданы и испытаны десятки генераторов псевдослучайных чисел. Работа этих генераторов основана на использовании формулы

X_i+1 =aX_i +C(mod m),

где a, c, m- константы, обычно автоматически вычисляемые в подпрограмме. На основе этого алгоритма разработана процедура URAND, которая приведена в приложении 1.1. Грин, Смит и Клем предложили аддитивный конгруэнтный метод. н основан на использовании рекуррентной формулы

X_i+1 =(X_i +X_i-1 )(mod m).

При X₀ =0 и X₁ =1 этот приводит к особому случаю, называемому последовательностью Фибоначчи.

Другие алгоритмы основаны на комбинации двух генераторов с перемешиванием получаемых последовательностей.

Поскольку при использовании детерминированных алгоритмов получаемая последовательность чисел является псевдослучайной, возникает вопрос: насколько они близки по своему поведению случайным? Для ответа на него предложено великое множество самых разнообразных методов статических испытаний.

Частотные тесты. Используют либо критерий хи-квадрат, либо критерий Колмогорова-Смирнова для сравнения близости распределения полученного набора чисел к равномерному распределению.

Весь диапазон чисел [0,1] разбивается на k интервалов. Статистика определяется выражением

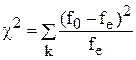
где f₀ -наблюдаемая частота для каждого интервала; f_e -ожидаемая частота для каждого интервала ( f_e =p*N, N-число опытов ).

Если =0, то наблюдаемые и теоретически предсказанные значения частот точно совпадают. Если >0, то расчётные значения сравниваются с табличными значениями _T . Значения _T табулированы для различных чисел степеней свободы v=r-1-m, где r-число интервалов, m-число параметров распределения, определяемых из опыта, и уровней доверительной вероятности 1-a. Если расчётная величина оказывается больше табличной, то между наблюдаемым и теоретическим распределением имеется значительное расхождение.

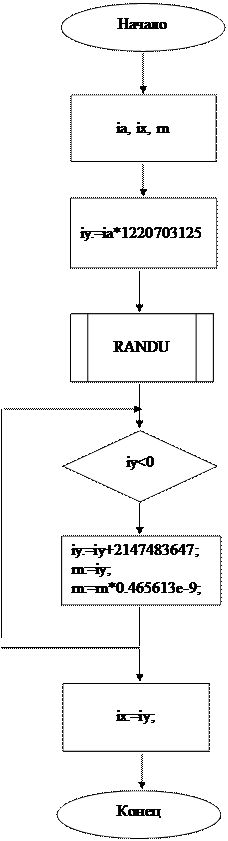Рисунок 1 – Схема алгоратма

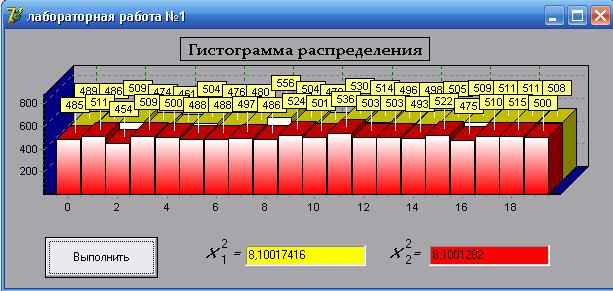
Рисунок 2 – Рабочая программа

Выводы: Изучение функционирования программных датчиков псевдослучайных чисел. Практическая проверка качества генераторов случайных чисел.

Методы получения на ЭВМ значений случайной величины, равномерно распределённой в интервале [0,1], можно разделить на три большие группы:

1. Использование физических датчиков (генераторов) случайных чисел.

2. Использование таблиц случайных чисел.

3. Получение псевдослучайных чисел.