Название: Системы счисления 6
Вид работы: реферат
Рубрика: Информатика
Размер файла: 19.17 Kb
Скачать файл: referat.me-132340.docx
Краткое описание работы: Введение. Системой счисления называется совокупность приемов наименования и записи чисел. В любой системе счисления для представления чисел выбираются некоторые символы (их называют цифрами), а остальные числа получаются в результате каких-либо операций над цифрами данной системы счисления.
Системы счисления 6
В ведение.
Системой счисления называется совокупность приемов наименования и записи чисел. В любой системе счисления для представления чисел выбираются некоторые символы (их называют цифрами ), а остальные числа получаются в результате каких-либо операций над цифрами данной системы счисления.
Система называется позиционной , если значение каждой цифры (ее вес) изменяется в зависимости от ее положения (позиции) в последовательности цифр, изображающих число.
Число единиц какого-либо разряда, объединяемых в единицу более старшего разряда, называют основанием позиционной системы счисления . Если количество таких цифр равно P , то система счисления называется P -ичной. Основание системы счисления совпадает с количеством цифр, используемых для записи чисел в этой системе счисления.
Запись произвольного числа x в P -ичной позиционной системе счисления основывается на представлении этого числа в виде многочлена
x = an Pn + an -1 Pn -1 + … + a 1 P 1 + a 0 P 0 + a -1 P -1 + … + a-m P-m
Арифметические действия над числами в любой позиционной системе счисления производятся по тем же правилам, что и десятичной системе, так как все они основываются на правилах выполнения действий над соответствующими многочленами. При этом нужно только пользоваться теми таблицами сложения и умножения, которые соответствуют данному основанию P системы счисления.
Постановка задачи.
Программа должна считывать из файла вещественные числа с фиксированной точкой в десятиричной системе. Затем, следуя заданию, необходимо перевести числа в шестнадцатеричную систему счисления и вывести результат в файл. Далее осуществляется перевод в восьмеричную систему счисления и выполняются две операции: сложение и вычитание. Результаты этих действий перевести обратно в шестнадцатиричнуюсистему счисления,а затем в десятичную и вывести в файл.
Правила перевода чисел.
Правило перевода из шестнадцатеричной в восьмеричную систему счисления.
Оптимальный способ перевода числа из шестнадцатеричной в восьмеричную систему счисления будет следующим. Т.к. шестнадцатеричное число имеет основание системы счисления 16=24 , а восьмеричное 8=23 , то шестнадцатеричное число переводим в двоичное: каждую цифру заменяем на группу из 4-х двоичных цифр ( тетраду ) соответственно данной таблице:
С и с т е м а с ч и с л е н и я |
С и с т е м а с ч и с л е н и я |
|||
| 2 | 16 | 2 | 16 | |
| 0000 | 0 | 1000 | 8 | |
| 0001 | 1 | 1001 | 9 | |
| 0010 | 2 | 1010 | A | |
| 0011 | 3 | 1011 | B | |
| 0100 | 4 | 1100 | C | |
| 0101 | 5 | 1101 | D | |
| 0110 | 6 | 1110 | E | |
| 0111 | 7 | 1111 | F | |
| Таблица №1 | ||||
Затем получившееся двоичное число разбиваем на группы по 3 цифры (триады). Далее заменяем эти триады цифры соответствующими восьмеричными цифрами. При необходимости добавить нули слева от числа для дробной части, и справа для целой части числа.
С и с т е м а с ч и с л е н и я |
С и с т е м а с ч и с л е н и я |
|||
| 2 | 8 | 2 | 8 | |
| 000 | 0 | 100 | 4 | |
| 001 | 1 | 101 | 5 | |
| 010 | 2 | 110 | 6 | |
| 011 | 3 | 111 | 7 | |
| Таблица №2 | ||||
Правило перевода из восьмеричной в шестнадцатеричную систему счисления.
Данный перевод осуществляется аналогично описанному в п. 3.1. с тем отличием, что восьмеричное число переводится в двоичное: каждая восьмеричная цифра заменяется двоичной триадой согласно таблице №2.
Затем двоичное число разбивается на тетрады (при необходимости добавить нули справа и слева от числа) которые заменяются шестнадцатеричными цифрами согласно таблице №1
Правило перевода из десятичной в любую другую систему счисления.
Перевод числа из десятичной системы в другую осуществляется с помощью деления десятичного числа на основание системы счисления, в которую переводится число. Полученные остатки от деления необходимо записать в обратном порядке. Полученное из остатков от деления число и будет являтся передставленим данного числа в системы, на основание которой делили.
Укрупненная схема алгоритма.
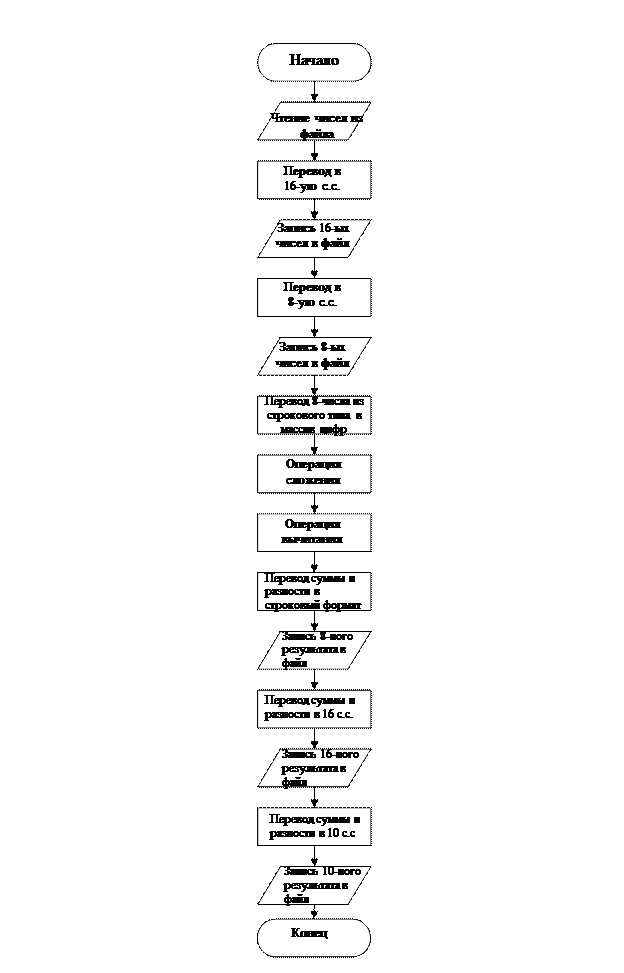
Похожие работы
-
Примеры выполнения заданий по программированию
1. Переведите данное число из десятичной системы счисления в двоично-десятичную. В двоично-десятичном представлении каждая цифра числа кодируется по
-
Двоичная система счисления
Контрольная работа №1 по дисциплине «Информатика» Двоичная система счисления Перевести из 10 в двоичную систему счисления цифры, согласно варианта.
-
Контрольная по информатике
КОНТРОЛЬНАЯ РАБОТА ПО ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКЕ ПРОГРАМИРОВАНИЮ Студентки I-го курса МГТУ ГА Шифр – э991613 2000 г. ироковой С.Х. Задание Перевести десятичное число в систему счисления с основанием “b”.
-
Позиционные системы исчисления Двоичная система счисления
Министерство науки и образования Украины Кафедра технической информатики Контрольная работа № 1 На тему: “Позиционные системы исчисления. Двоичная система счисления.”
-
Системы счисления 5
Системой счисления называется совокупность приемов наименования и записи чисел. В любой системе счисления для представления чисел выбираются некоторые символы (их называют цифрами), а остальные числа получаются в результате каких-либо операций над цифрами данной системы счисления.
-
Позиционные системы счисления
Перевод чисел из одной позиционной системы счисления в другую Арифметические операции с числами в позиционных системах счисления Системой счисления называется совокупность приемов наименования и записи чисел. В любой системе счисления для представления чисел выбираются некоторые символы (их называют цифрами), а остальные числа получаются в результате каких-либо операций над цифрами данной системы счисления.
-
Система счисления 2
Содержание Система счисления — это совокупность приемов и правил, по которым числа записываются и читаются. 2 Как порождаются целые числа в позиционных системах счисления? 2
-
Разработка электронных таблиц
Федеральное агентство по образованию ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ "ОМСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ" (ОмГТУ)
-
Выполнение арифметических операций над числами с фиксированной запятой
Цель: ознакомиться с командами арифметических операций, вводом данных с клавиатуры и выводом данных на экран. Задание: написать программу ввода с клавиатуры двух чисел в 9-ричной системе счисления размером с слово, выполнения над ними деления и вывода результата в исходной системе счисления. Программа должна предусматривать контроль вводимой информации, контроль диапазона чисел и результата операции (переполнение, невозможность деления).
-
Действия над числами в различных системах счисления
В заданиях 3-5 проверять правильность вычисления переводом исходных данных и результатов в двоичную систему счисления. В задании 1д получить пять знаков после запятой в двоичном представлении.