Название: Построение логической модели исследуемой системы
Вид работы: дипломная работа
Рубрика: Информатика
Размер файла: 25.29 Kb
Скачать файл: referat.me-132508.docx
Краткое описание работы: Тульский институт экономики и информатики Кафедра информационных технологий Контрольная работа По дисциплине: Интеллектуальные информационные системы
Построение логической модели исследуемой системы
Тульский институт экономики и информатики
Кафедра информационных технологий
Контрольная работа
По дисциплине: Интеллектуальные информационные системы
На тему: «Построение логической модели исследуемой системы»
Выполнил: Андрианова К.Г.
гр.ТоПИвЭ-05
Проверил: Токарев В.Л.
Тула 2009 г.
Задание на работу
Дана выборка данных WN, объемом N=30, которая содержит информацию о трех входах системы (х1, х2, х3) и одном выходе (у), и представлена в виде матрицы размерностью 30´4. Причем значения в ней представлены для двух входных переменных в качественных шкалах (х1, х2), для третьей (х3) – в количественной (табл.1). Значения выходной переменной представлены в качественной шкале yÎ{A,B,C,D,E,}.
Требуется построить логическую модель вида:
И проверить адекватность модели по критерию
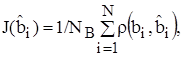
Обучающая выборка.
Таблица 1
| N: | x1 | x2 | x3 | y |
| 1 | E | D | -0.8 | D |
| 2 | E | D | 0.82 | E |
| 3 | E | D | -0.92 | A |
| 4 | E | D | 0.54 | E |
| 5 | E | A | -0.24 | F |
| 6 | A | D | 0.7 | F |
| 7 | C | D | -0.7 | D |
| 8 | E | C | -0.8 | D |
| 9 | E | D | 0.18 | D |
| 10 | E | C | -0.5 | E |
| 11 | C | D | -0.5 | D |
| 12 | E | D | 0.34 | E |
| 13 | E | A | 0.86 | F |
| 14 | E | A | 0.88 | F |
| 15 | E | A | 0.38 | F |
| 16 | C | D | -0.06 | D |
| 17 | E | D | -0.8 | A |
| 18 | A | D | -0.14 | D |
| 19 | E | A | -0.8 | E |
| 20 | E | D | 0.12 | D |
| 21 | E | A | -0.58 | F |
| 22 | D | D | -0.86 | A |
| 23 | E | A | 0.26 | F |
| 24 | E | D | -0.32 | D |
| 25 | A | A | 0.32 | F |
| 26 | A | C | -0.96 | E |
| 27 | E | A | -0.08 | F |
| 28 | A | D | 0.42 | F |
| 29 | A | D | -0.3 | E |
| 30 | D | D | -0.34 | D |
| 31 | A | D | -0.86 | D |
| 32 | C | D | 0.98 | F |
| 33 | D | C | 0.66 | F |
| 34 | A | D | 0.2 | E |
| 35 | C | C | -0.9 | E |
| 36 | C | C | -0.2 | F |
| 37 | E | C | -0.42 | E |
| 38 | C | D | 0.56 | E |
| 39 | C | A | 0.34 | F |
| 40 | D | A | -0.96 | E |
| 41 | A | A | 0.3 | F |
| 42 | D | C | 0.48 | F |
| 43 | E | D | -0.86 | D |
| 44 | E | D | 0.82 | F |
| 45 | E | D | -0.02 | D |
| 46 | E | D | -0.7 | A |
| 47 | D | D | -0.66 | D |
| 48 | E | D | 0.42 | F |
| 49 | A | A | 0.92 | F |
| 50 | E | D | -1 | D |
Решение.
| N: | x1 | x2 | x3 | y |
| 1 | E | D | -0.8 | D |
| 2 | E | D | 0.82 | E |
| 3 | E | D | -0.92 | A |
| 4 | E | D | 0.54 | E |
| 5 | E | A | -0.24 | F |
| 6 | A | D | 0.7 | F |
| 7 | C | D | -0.7 | D |
| 8 | E | C | -0.8 | D |
| 9 | E | D | 0.18 | D |
| 10 | E | C | -0.5 | E |
| 11 | C | D | -0.5 | D |
| 12 | E | D | 0.34 | E |
| 13 | E | A | 0.86 | F |
| 14 | E | A | 0.88 | F |
| 15 | E | A | 0.38 | F |
| 16 | C | D | -0.06 | D |
| 17 | E | D | -0.8 | A |
| 18 | A | D | -0.14 | D |
| 19 | E | A | -0.8 | E |
| 20 | E | D | 0.12 | D |
| 21 | E | A | -0.58 | F |
| 22 | D | D | -0.86 | A |
| 23 | E | A | 0.26 | F |
| 24 | E | D | -0.32 | D |
| 25 | A | A | 0.32 | F |
| 26 | A | C | -0.96 | E |
| 27 | E | A | -0.08 | F |
| 28 | A | D | 0.42 | F |
| 29 | A | D | -0.3 | E |
| 30 | D | D | -0.34 | D |
1. По таблице определяем диапазон изменения значений х3 : [-1; +1].
2. С целью определения непересекающихся подмножеств GI , упоря-
дочим матрицу W30 по значениям качественных переменных.
| 25 | А | А | 0.32 | F |
| 26 | A | C | -0.96 | E |
| 6 | A | D | 0.7 | F |
| 18 | A | D | -0.14 | D |
| 28 | A | D | 0.42 | F |
| 29 | A | D | -0.3 | F |
| 7 | C | D | -0.7 | D |
| 11 | C | D | -0.5 | D |
| 16 | C | D | -0.06 | D |
| 22 | D | D | -0.86 | A |
| 30 | D | D | -0.34 | D |
| 5 | E | A | -0.24 | F |
| 13 | E | A | 0.86 | F |
| 14 | E | A | 0.88 | F |
| 15 | E | A | 0.38 | F |
| 19 | E | A | -0.8 | E |
| 21 | E | A | -0.58 | F |
| 23 | E | A | 0.26 | F |
| 27 | E | A | -0.08 | F |
| 8 | E | C | -0.8 | D |
| 10 | E | C | -0.5 | E |
| 1 | E | D | -0.8 | D |
| 2 | E | D | 0.82 | E |
| 3 | E | D | -0.92 | A |
| 4 | E | D | 0.54 | E |
| 9 | E | D | 0.18 | D |
| 12 | E | D | 0.34 | E |
| 17 | E | D | -0.8 | A |
| 20 | E | D | 0.12 | D |
| 24 | E | D | -0.32 | D |
Объединив некоторые значения количественной переменной в интервалы, получим модель в матричном виде, соответствующую обучающей выборке.
| 25 | A | A | 0.3 … 0.92 | F |
| 26 | A | C | -0.96 | E |
| 6 | A | D | -0.3 … 0.7 | F |
| 18 | A | D | -0.14 ..-0.86 | D |
| 11 | C | D | -0.06 .. -0.7 | D |
| 22 | D | D | -0.86 | A |
| 30 | D | D | -0.34 .. -0.66 | D |
| 15 | E | A | -0.08 .. 0.88 | F |
| 19 | E | A | -0.8 | E |
| 8 | E | C | -0.8 | D |
| 10 | E | C | -0.42 … -0.5 | E |
| 1 | E | D | -1…0.18 | D |
| 2 | E | D | 0.34 .. 0.82 | E |
| 3 | E | D | -0.7..-0.92 | A |
3. Определим непересекающиеся множества значений обучающей выборки путем определения интервалов значений количественной переменной как окрестностей точек обучающей выборки для каждой конъюнкции качественных переменных.
| 25 | A | A | 0 …. 1 | F |
| 26 | A | C | -1 …. 0 | E |
| 18 | A | D | -1 .. -0.23 | D |
| 6 | A | D | -0.23 .., 1 | F |
| 11 | C | D | -1 … 0 | D |
| 22 | D | D | -0.56…1 | A |
| 30 | D | D | -1 .. -0.56 | D |
| 19 | E | A | -1 …- 0.45 | E |
| 15 | E | A | -0.45 .. 1 | F |
| 8 | E | C | -1 .. -0.25 | D |
| 10 | E | C | -0.25 .. 1 | E |
| 3 | E | D | -0.87..0.1 | A |
| 1 | E | D | -1…-0.87 0.1 … 0.21 |
D |
| 2 | E | D | 0.21 …1 | E |
4. Получим первое приближение логической модели.
| 25 | A | A | 0 …. 1 | F |
| 26 | A | C | -1 …. 0 | E |
| 18 | A | D | -1 .. -0.23 | D |
| 6 | A | D | -0.23 .., 1 | F |
| 11 | C | D | -1 … 0 | D |
| 22 | D | D | -1…-0.6 | A |
| 30 | D | D | -0.6…1 | D |
| 19 | E | A | -1 …- 0.08 | E |
| E | A | -0.08..-0.45 | F | |
| 15 | E | A | -0.45 .. 1 | F |
| 8 | E | C | -1 .. -0.25 | D |
| E | C | -0.25..-0.42 | E | |
| 10 | E | C | -0.42 .. 1 | E |
| 3 | E | D | -1…-0.8 | A |
| 1 | E | D | -0.8…0.27 | D |
| 2 | E | D | 0.27 …1 | E |
Похожие работы
-
Изучение возможностей экспертных систем
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ СТАРООСКОЛЬСКИЙ ТЕХНОЛОГИЧЕСКИЙ ИНСТИТУТ (ФИЛИАЛ) МОСКОВСКОГО ГОСУДАРСТВЕННОГО ИНСТИТУТА СТАЛИ И СПЛАВОВ
-
Информационные технологии в экономике 3
Федеральное агенство по образованию Государственное образовательное учреждение высшего профессионального образования «Российский государственный профессионально-педагогический университет»
-
Обработка двумерных массивов матриц .
МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ЭКОНОМИКИ, СТАТИСТИКИ И ИНФОРМАТИКИ. КАФЕДРА МАТЕМАТИЧЕСКОГО ОБЕСПЕЧЕНИЯ И АДМИНИСТРИРОВАНИЯ ИНФОРМАЦИОННЫХ СИСТЕМ.
-
Решение практической задачи на паскале
ГОУ ВПО «Московский государственный открытый университет» Чебоксарский политехнический институт (филиал) Кафедра информационных технологий и программирования
-
Основные информационные процессы
ИНСТИТУТ ЭКОНОМИКИ УПРАВЛЕНИЯ И ПРАВА ФАКУЛЬТЕТ МЕНЕДЖМЕНТА И МАРКЕТИНГА КАФЕДРА ИНФОРМАТИКИ И МАТЕМАТИКИ КОНТРОЛЬНАЯ РАБОТА Вариант 4 Выполнила студент гр. 761у
-
по Информатике 8
МИНИСТЕРСТВО ФИНАНСОВ ПРАВИТЕЛЬСТВА МОСКОВСКОЙ ОБЛАСТИ РОССИЙСКОЙ ФЕДЕРАЦИИ КОРОЛЁВСКИЙ ИНСТИТУТ УПРАВЛЕНИЯ, ЭКОНОМИКИ И СОЦИОЛОГИИ Кафедра информатики Контрольная работа
-
Продукционные модели представления знаний
КОНТРОЛЬНАЯ РАБОТА «Продукционные модели представления знаний» по дисциплине Интеллектуальные информационные системы Санкт-Петербург 2010 Продукционные модели
-
Вычисление определенного интеграла методом трапеций
Министерство образования Российской Федерации Тульский государственный университет Кафедра "Инструментальные и метрологические системы"
-
Подготовка электронных документов в MS Word 2
НОУ ВПО ТУЛЬСКИЙ ИНСТИТУТ УПРАВЛЕНИЯ И БИЗНЕСА им. Н. Д. Демидова ОТЧЕТ о выполнении компьютерного практикума по дисциплине “Информатика” “Подготовка электронных документов в MS Word”
-
Изображение движущегося объекта на фоне неподвижных предметов
Московская открытая социальная академия Финансово-экономический факультет Кафедра информационных технологий в экономике К У Р С О В А Я Р А Б О Т А по дисциплине