Название: Логические формулы и операции Виды и правила вопросов

Вид работы: реферат

Рубрика: Логика

Размер файла: 413.58 Kb

Скачать файл: referat.me-204043.docx

Краткое описание работы: Логические операции Каждая логическая связка рассматривается как операция над логическими высказываниями и имеет свое название и обозначение. Выделяют следующие логические операции: инверсия; конъюнкция; дизъюнкция; импликация; эквиваленция.

Логические формулы и операции Виды и правила вопросов

Логические операции .

Каждая логическая связка рассматривается как операция над логическими высказываниями и имеет свое название и обозначение.

Выделяют следующие логические операции: инверсия; конъюнкция; дизъюнкция; импликация; эквиваленция.

1. Операция инверсия (отрицание):

Отрицание - это логическая операция, которая каждому простому высказыванию ставит в соответствие составное высказывание, заключающееся в том, что исходное высказывание отрицается.

Обозначается:

В естественном языке: соответствует словам "неверно, что..." и частице "не"

Диаграмма Эйлера-Венна:

Принимаемые значения:

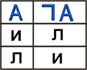
Диаграмма Эйлера-Венна: В алгебре множеств логическому отрицанию соответствует операция дополнения до универсального множества, т.е. множеству получившемуся в результате отрицания множества соответствует множество, дополняющее его до универсального множества.

Пример: Луна — спутник Земли (А) . Луна — не спутник Земли ( A)

2. Операция конъюнкция (лат. conjunctio — соединение) (логическое умножение):

Конъюнкция - это логическая операция, ставящая в соответствие каждым двум простым высказываниям составное высказывание, являющееся истинным тогда и только тогда, когда оба исходных высказывания истинны.

Обозначается:

В естественном языке: соответствует союзу "и"

Принимаемые значения:

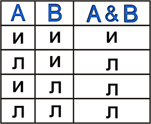
Диаграмма Эйлера-Венна: В алгебре множеств конъюнкции соответствует операция пересечения множеств, т.е. множеству получившемуся в результате умножения множеств А и В соответствует множество, состоящее из элементов, принадлежащих одновременно двум множествам.

Примеры:

1. 10 делится на 2 (A - и) . 5 больше 3 (B - и) . 10 делится на 2 и 5 больше 3 (A B - и) .

2. 10 не делится на 2 (A - л) . 5 больше 3 (B - и) . 10 не делится на 2 и 5 больше 3 (A B - л) .

3. 10 делится на 2 (A - и) . 5 не больше 3 (B - л) . 10 делится на 2 и 5 не больше 3 (A B - л) .

4. 10 не делится на 2 (A - л) . 5 не больше 3 (B - л) . 10 делится на 2 и 5 больше 3 (A B - л) .

3. Операция дизъюнкция (лат. disjunctio — разделение) (логическое сложение):

Дизъюнкция - это логическая операция, которая каждым двум простым высказываниям ставит в соответствие составное высказывание, являющееся ложным тогда и только тогда, когда оба исходных высказывания ложны и истинным, когда хотя бы одно из двух образующих его высказываний истинно.

Обозначается:

В естественном языке: соответствует союзу "или"

Принимаемые значения:

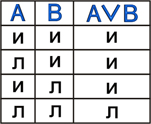
Диаграмма Эйлера-Венна: В алгебре множеств дизъюнкции соответствует операция объединения множеств, т.е. множеству получившемуся в результате сложения множеств А и В соответствует множество, состоящее из элементов, принадлежащих либо множеству А, либо множеству В.

Примеры:

1. 10 делится на 2 (A - и) . 5 больше 3 (B - и) . 10 делится на 2 или 5 больше 3 (A B - и) .

2. 10 не делится на 2 (A - л) . 5 больше 3 (B - и) . 10 не делится на 2 или 5 больше 3 (A B - и) .

3. 10 делится на 2 (A - и) . 5 не больше 3 (B - л) . 10 делится на 2 или 5 не больше 3 (A B - и) .

4. 10 не делится на 2 (A - л) . 5 не больше 3 (B - л) . 10 не делится на 2 или 5 не больше 3 (A B - л) .

4. Операция импликация (лат. лат. implico — тесно связаны) (логическое сложение):

Импликация - это логическая операция, ставящая в соответствие каждым двум простым высказываниям составное высказывание, являющееся ложным тогда и только тогда, когда условие (первое высказывание) истинно, а следствие (второе высказывание) ложно.

Обозначается: о

В естественном языке: соответствует обороту "если ..., то ..."

Принимаемые значения: л

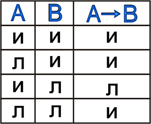
Примеры:

1. Данный четырёхугольник — квадрат (A - и) . Около данного четырёхугольника можно описать окружность (B - и) . Если данный четырёхугольник квадрат, то около него можно описать окружность (A B - и) .

2. Данный четырёхугольник — не квадрат (A - л) . Около данного четырёхугольника можно описать окружность (B - и) . Если данный четырёхугольник не квадрат, то около него можно описать окружность (A B - и) .

3. Данный четырёхугольник — квадрат (A - и) . Около данного четырёхугольника нельзя описать окружность (B - л) . Если данный четырёхугольник квадрат, то около него можно описать окружность (A B - л) .

4. Данный четырёхугольник — не квадрат (A - л) . Около данного четырёхугольника нельзя описать окружность (B - л) . Если данный четырёхугольник не квадрат, то около него нельзя описать окружность (A B - и) .

5. Операция эквиваленция (двойная импликация):

Эквиваленция – это логическая операция, ставящая в соответствие каждым двум простым высказываниям составное высказывание, являющееся истинным тогда и только тогда, когда оба исходных высказывания одновременно истинны или одновременно ложны.

Обозначается: о

В естественном языке: соответствует оборотам речи "тогда и только тогда" ; "в том и только в том случае"

Принимаемые значения:

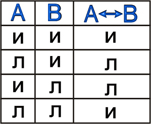
Примеры:

1. 24 делится на 6 (A - и) . 24 делится на 3 (B - и) . 24 делится на 6 тогда и только тогда, когда 24 делится на 3 (A B - и) .

2. 24 не делится на 6 (A - л) . 24 делится на 3 (B - и) . 24 не делится на 6 тогда и только тогда, когда 24 делится на 3 (A B - л) .

3. 24 делится на 6 (A - и) . 24 не делится на 3 (B - л) . 24 делится на 6 тогда и только тогда, когда 24 делится на 3 (A B - л) .

4. 24 не делится на 6 (A - л) . 24 не делится на 3 (B - л) . 24 не делится на 6 тогда и только тогда, когда 24 не делится на 3 (A B - и) .

Порядок выполнения логических операций задается круглыми скобками. Но для уменьшения числа скобок договорились считать, что сначала выполняется операция отрицания (“не”), затем конъюнкция (“и”), после конъюнкции — дизъюнкция (“или”) и в последнюю очередь — импликация и эквиваленция.

Логические формулы.

С помощью логических переменных и символов логических операций любое высказывание можно формализовать, то есть заменить логической формулой.

Определение логической формулы:

1. Всякая логическая переменная и символы "истина" ("1" ) и "ложь" ("0" ) — формулы.
2. Если А и В — формулы, то , (А &В) , (А v В) , (А B) , (А В) — формулы.
3. Никаких других формул в алгебре логики нет.

В п. 1 определены элементарные формулы; в п. 2 даны правила образования из любых данных формул новых формул.

Пример:

Рассмотрим высказывание "если я куплю яблоки или абрикосы, то приготовлю фруктовый пирог" .

Обозначим буквой A высказывание: "купить яблоки" , буквой B - высказывание: "купить абрикосы" , буквой C - высказывание: "испечь пирог".

Тогда высказывание "если я куплю яблоки или абрикосы, то приготовлю фруктовый пирог" формализуется в виде формулы:

(A v B) C

Формула выполнимая - если при определенных сочетаниях значений переменных она принимает значение "истина" ("1" ) или "ложь" ("0" ).

Как показывает анализ формулы (A v B) C , при определённых сочетаниях значений переменных A , B и C она принимает значение "истина" , а при некоторых других сочетаниях — значение "ложь" .

Некоторые формулы принимают значение “истина” при любых значениях истинности входящих в них переменных. Таковой будет, например, формула А v A , соответствующая высказыванию “Этот треугольник прямоугольный или косоугольный” . Эта формула истинна и тогда, когда треугольник прямоугольный, и тогда, когда треугольник не прямоугольный.

Тавтология - тождественно истинная формула, или формула принимающая значение "истина" ("1" ) при любых входящих в нее значениях переменных.

Логически истинные высказывания - высказывания, которые формализуются тавтологиями.

В качестве другого примера рассмотрим формулу А & A , которой соответствует, например, высказывание “Катя самая высокая девочка в классе, и в классе есть девочки выше Кати” . Очевидно, что эта формула ложна, так как либо А , либо A обязательно ложно.

Противоречие - тождественно ложная формула, или формула принимающая значение "ложь" ("0" ) при любых входящих в нее значениях переменных.

Логически ложные высказывания - высказывания, которые формализуются противоречиями.

Равносильные формулы - две формулы А и В принимающие одинаковые значения, при одинаковых наборах значений входящих в них переменных.

Равносильность двух формул алгебры логики обозначается символом .

Равносильное преобразование формулы - замена формулы другой, ей равносильной.