Название: Надежность турбобура

Вид работы: реферат

Рубрика: Маркетинг

Размер файла: 222.56 Kb

Скачать файл: referat.me-209707.docx

Краткое описание работы: Введение 1 Законы распределения случайных величин Обработка информации о надежности буровых машин Анализ статистического материала В таблице 1 представлено распределение наработок до отказа бура.

Надежность турбобура

Введение

1 Законы распределения случайных величин

2 Обработка информации о надежности буровых машин

2.1 Анализ статистического материала

В таблице 1 представлено распределение наработок до отказа бура.

Таблица 1 Частота наработки турбобура до отказа

ti	Частота ni	ti	Частота ni	ti	Частота ni	ti	Частота ni	ti	Частота ni	ti	Частота ni
1	1	24	1	47	1	70	2	93	2	116	0
2	3	25	6	48	1	71	1	94	2	117	0
3	1	26	2	49	2	72	1	95	1	118	0
4	1	27	1	50	5	73	4	96	0	119	0
5	0	28	3	51	0	74	2	97	3	120	0
6	2	29	1	52	2	75	1	98	2	121	0
7	2	30	1	53	1	76	3	99	1	122	0
8	0	31	2	54	3	77	1	100	0	123	0
9	2	32	0	55	0	78	1	101	0	124	0
10	1	33	1	56	1	79	1	102	1	125	0
11	3	34	4	57	5	80	2	103	1	126	0
12	1	35	1	58	4	81	0	104	1	127	0
13	2	36	3	59	3	82	3	105	0	128	0
14	3	37	1	60	1	83	2	106	0	129	0
15	2	38	0	61	0	84	2	107	0	130	0
16	0	39	4	62	2	85	1	108	0	131	0
17	2	40	1	63	4	86	0	109	1	132	0
18	2	41	1	64	2	87	1	110	1	133	1
19	3	42	2	65	2	88	3	111	0	134	0
20	1	43	0	66	2	89	1	112	0	135	0
21	2	44	10	67	2	90	1	113	0	136	1
22	1	45	1	68	0	91	2	114	0
23	0	46	1	69	1	92	3	115	1

t_i –наработка турбобура до отказа

n_i -частота

∑n_i =183

Построение вариационного ряда

Строим путем ранжирования

Вариационный ряд: 1,2,2,2,3,4,6,6,7,7,9,9,10,11,11,11,12,13,13,14,14,14, 15,15,17,17,18,18,19,19,19,20,21,21,22,24,25,25,25,25,25,25,26,26,27,28,28,28,29, 30,31,31,33,34,34,34,34,35,36,36,36,37,39,39,39,39,40,41,42,42,44,44,44,44,44,44,44,44,44,44,45,46,36,47,48,49,49,50,50,50,50,50,52,52,53,54,54,54,56,57,57,57,57,57,58,58,58,58,59,59,59,49,60,62,62,63,63,63,63,64,64,65,65,66,66,67,67,69,70,70,71,72,73,73,73,73,74,74,75,76,76,76,77,78,79,80,80,82,82,82,83,83,84,84,85,87,88,88,88,89,90,91,91,92,92,92,93,93,94,94,95,97,97,97,98,98,99,102,103,104,109,110,115,133,136.

2.2 Построение статистического ряда

Для облегчения расчетов при числе информации n > 25 статистический материал обычно представляется в виде статистического ряда.

Число интервалов ряда принимается равным

Рекомендуется принимать от 6 до 20 интервалов. Интервалы ряда принимает равными, но допускается объединять интервалы и принимать их равной величины, если количество наблюдений в ин­тервале меньше пяти. Примем k=14

Величину одного интервала определяем по выражению:

где - наибольшее значение случайной величины;

- наименьшее значение случайной величины;

- ширина интервала.

Принимаем

При составлении статистического ряда для каждого интервала подсчитывают:

n_i - количество значений случайной величины в в i – ом интервале (частость)

- частость в i – ом интервале

- накопленная частость ;

- эмпирическая плотность вероятности , где - ширина интервала.

По данным таблицы (1) был построен статистический интервальный ряд – таблица 2.

Таблица 2 Статистический интервальный ряд

№	Интервал, ч	∆t	Середина	n* i	p* i
1	0-10	10	5	16	0,0804
2	10-20	10	15	26	0,1307
3	20-30	10	25	24	0,1206
4	30-40	10	35	23	0,1156
5	40-50	10	45	23	0,1156
6	50-60	10	55	29	0,1457
7	60-70	10	65	12	0,0603
8	70-80	10	75	22	0,1106
9	80-90	10	85	5	0,0251
10	90-100	10	95	10	0,0503
11	100-110	10	105	4	0,0201
12	110-120	10	115	2	0,0101
13	120-130	10	125	2	0,0101
14	130-140	10	135	1	0,0050

Так как частота в интервалах 11-14 меньше пяти, то объединяем их в один интервал:

n₁₁ =8 [100-140]

Итоговый интервальный ряд представлен в таблице 3.

Таблица 3 Итоговый статистический интервальный ряд

№	Интервал, ч	∆t	Середина	n* i	p* i
1	0-10	10	5	16	0,0804
2	10-20	10	15	26	0,1307
3	20-30	10	25	24	0,1206
4	30-40	10	35	23	0,1156
5	40-50	10	45	23	0,1156
6	50-60	10	55	29	0,1457
7	60-70	10	65	12	0,0603
8	70-80	10	75	22	0,1106
9	80-90	10	85	5	0,0251
10	90-100	10	95	10	0,0503
11	100-140	40	120	9	0,0452

2.3 Расчет параметров статистического распределения

Функция распределения случайной величины может быть достачно строго определена о помощью статистических характеристик, называемых параметрами распределения.

Распределение случайных величин, изучаемых в теории надёжности характеризуют с помощью математического ожидания, дисперсии, среднеквадратического отклонения и коэффициентов вариации.

Математическим ожиданием случайной величины называется сумма произведений всех возможных значений случайной величины на вероятность этих величин [ 2 ]

На практике для оценки математического ожидания используют сред­нее, арифметическое значение случайной величины.

Если п<25; , то среднее значение определяет по формуле

где п - количество; информации;

t_i - значение i - гo показателя надежности.

Для статистического ряда

где k - количество интервалов в статистическом раду;

- значение середины i -го интервала;

- опытная вероятность i -го интервала.

Важным параметром распределения является дисперсия. Диспер­сия характеризует разбросанность значений случайной величины около ее математического ожидания. Дисперсия имеет размерность квад­рата случайной величины, потому часто, пользуются среднеквадратическим отклонением случайной

где - среднее квадратическое отклонение;

- дисперсия случайной величины.

Среднее квадратическое отклонение определяют по уравнению (при n<25)

Если используется статистический ряд , то среднее квадратическое отклонение равно

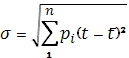
Используя данные таблицы 2 определим математическое ожидание и дисперсию для этого построим таблицу 4.

Таблица 4 Вспомогательные данные для расчета статистических показателей

интервал
1	0,340314	-40,1571	1612,59	109,75744
2	2,041885	-30,1571	909,4488	123,79931
3	4,581152	-20,1571	406,3074	74,454234
4	4,947644	-10,1571	103,166	14,58368
5	6,125654	-0,15707	0,02467	0,0033583
6	4,319372	9,842932	96,88331	7,6086368
7	3,403141	19,84293	393,7419	20,614762
8	3,926702	29,84293	890,6006	46,628303
9	4,005236	39,84293	1587,459	74,801744
10	3,481675	49,84293	2484,318	91,048299
11	2,748691	59,84293	3581,177	93,748076
Сумма	45,15707	-	-	924,0591

Определим математическое ожидание и среднее квадратическое отклонение

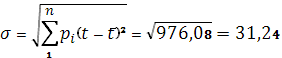
2.4 Оценка резко выделяющихся значений

Статистическая информация может содержать резко выделяющиеся значения, которые оказывают существенное влияние на оцен­ку показателей надёжности, поэтому все резко выделяющиеся значения случайной величины должны быть проанализированы и исключены из рассмотрения, если они является следствием грубых ошибок при наблюдении. Однако известны случаи, когда необоснован­но отбрасываются результаты наблюдений, которые якобы наруша­ет вид исследуемого процесса, что может привести к неверным выводам, особенно при малой выборке. В связи с этим при исключении из рассмотрения отдельных результатов нужно тщательно проанализировать условия проведения наблюдений, физическую кар­тину процесса. Большой разброс значений может быть и следствием резко меняющихся условий эксплуатации, некачественной техноло­гией изготовления изделия. Приближенно оценку информации на выпадающие точки проверят по правилу . Если значения случайной величины не выхо­дят за пределы , все точки информации считает действи­тельными.

Произведем оценку информации на выпадении

Все точки действительны, поскольку все значения работы на отказ турбобура меньше 150,05

Расчет по критерию Романовского. Рассматриваем и без учета сомнительных членов ряда распределения . Если ,то с выбранной вероятностью данные члены можно исключить из рассмотрения. Сомнительные члены: 133, 136.

Рассчитаем параметры статистического распределения без сомнительных членов.

Примем k=13,тогда . Принимаем ∆t=9. В таблицах 5, 6 представлены статистические интервальные ряды без сомнительных членов, исходный и преобразованный.

Таблица 5 – статистический интервальный ряд без сомнительных членов совокупности

№	Интервал, ч	∆t	Середина	n* i	p* i
1	0-9	9	4,5	12	0,0663
2	9-18	9	13,5	16	0,0884
3	18-27	9	22,5	17	0,0939
4	27-36	9	31,5	16	0,0884
5	36-45	9	40,5	20	0,1105
6	45-54	9	49,5	16	0,0884
7	54-63	9	58,5	20	0,1105
8	63-72	9	67,5	13	0,0718
9	72-81	9	76,5	15	0,0829
10	81-90	9	85,5	14	0,0773
11	90-99	9	94,5	16	0,0884
12	99-108	9	103,5	3	0,0166
13	108-117	9	112,5	3	0,0166
14	117-126	6	121,5	12	0,0663

Таблица 6 – Преобразованный статистический интервальный ряд без сомнительных членов совокупности

№	Интервал, ч	∆t	Середина	n* i	p* i
1	0-9	9	4,5	11	0,0582
2	9-18	9	13,5	25	0,1323
3	18-27	9	22,5	25	0,1323
4	27-36	9	31,5	28	0,1481
5	36-45	9	40,5	31	0,1640
6	45-54	9	49,5	9	0,0476
7	54-63	9	58,5	15	0,0794
8	63-72	9	67,5	9	0,0476
9	72-81	9	76,5	9	0,0476
10	81-90	9	85,5	9	0,0476
11	90-99	9	94,5	6	0,0317
12	99-108	9	103,5	6	0,0317
13	108-126	9	117	6	0,0317

Среднее значение:

Среднеквадратическое отклонение:

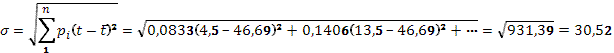
Проверяем t=133:

Проверяем t=136:

Следовательно, член 133 и 136 по критерию Романовского можно исключить из дальнейшего рассмотрения.

Критерий Ирвина.

Рассчитаем критерий Ирвина для сомнительных членов совокупности:

Следовательно, анализируемые величины оставляем при дальнейшем рассмотрении.

Критерий Груббса:

Для наименьшей точки информации:

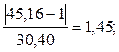
Для наибольшей точки информации:

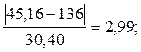
Так как для обеих точек при n=191 заведомо (таблица 5 приложения), то оставляем крайние точки в рассматриваемой совокупности.

Сомнительные члены удовлетворяют 3 из 4 критериев. Кроме того, известно, что турбобур работает в резко меняющихся условиях эксплуатации и исключение крайних точек искажает картину отказов двигателя, поэтому сомнительные члены включаем в общую совокупность.

Таким образом, для дальнейших расчетов используем статистический интервальный ряд, представленный в таблице 3.

2.5 Выбор теоретического закона распределения

Вероятность безотказной работы в первом приближении дают представление о распределении показателя надежности.Однако в статистическом материале из – за ограниченного числа наблюдений всегда присутствуют элементы случайности. При обработке статистического материала важной задачей является подбор теоретического закона распределения наилучшим образом описывающим статистическое распределение [ 2 ] , выражающим его существенные черты без элемента случайности.

Теоретический закон подбирают , принимая во внимание :

· физическую природу явления отказов;

· опыт отработки деталей и изделий аналогичного назначения;

· форму кривой плотности распределения;

· совпадение опытных точек с теоретической кривой интегральной функции или функции безотказности;

· коэффициент вариации.

Значение коэффициента вариации, характеризующего расслаивание показателя надежности:

уже позволяет судить об условиях эксплуатации машин и их технологии изготовления [8, 10] . Разработаны таблицы [10] , позволяющие ориентировочно судить о виде закона распределения в зависимости от величины коэффициента вариации ( тал. 7 и 8 приложения).

Авторы [ 8 ] рекомендуют для машин в первом приближении принимать нормальный закон приближения , если , и распределение Вейбулла, если . Когда коэффициент вариации изменяется в пределах 0,30 – 0,50 , то выбирают тот закон , который дает лучшее совпадение по критериям согласия.

Выберем теоретический закон распределения, определим доверительные границы среднего значения показателя надежности.

Анализ причин отказов турбобуров показывает, что они связаны как с приработочными , усталостными , так и с износовыми отказами. Режим работы турбобура меняется в широких пределах , на что указывает и значение коэффициента вариации, поэтому можно сделать предположение, что наработка турбобура до отказа описывается распределением Вейбулла.

По табл.2 приложения определяем параметры распределения Вейбулла . Для коэффициента вариации

Параметр а подсчитываем по выражению (13)

Теоретическая функция плотности распределения f(t) и вероятность безотказной работы p(t) будут иметь вид

В таблице 7 приведены теоретические параметры статистического ряда, рассчитанные по вышеприведенным формулам.

Таблица 7 – Теоретические параметры распределения

t	f(t)	F(t)	P(t)
0	0	0	1	0
5	0,0093	0,0315	0,9685	0,0096
15	0,0141	0,1533	0,8467	0,0166
25	0,0150	0,3009	0,6991	0,0215
35	0,0140	0,4473	0,5527	0,0254
45	0,0121	0,5787	0,4213	0,0288
55	0,0099	0,6890	0,3110	0,0319
65	0,0077	0,7770	0,2230	0,0346
75	0,0058	0,8443	0,1557	0,0372
85	0,0042	0,8940	0,1060	0,0396
95	0,0030	0,9295	0,0705	0,0419
105	0,0020	0,9541	0,0459	0,0440
125	0,0009	0,9817	0,0183	0,0480

2.1 Построение графиков теоретических и статистических функций

Статистический ряд позволяет построить интегральную функцию распределений и обратную интегральную функцию распределения функцию распределения и обратную интегральную функцию распределения функции “ отказности “ и “ безотказности “.

По данным статистического ряда и теоретического распределения строим графики статистических и теоретических функций показателя надежности. Дифференциальная функция f(t) наиболее наглядно отражает специфические черты закона распределения.

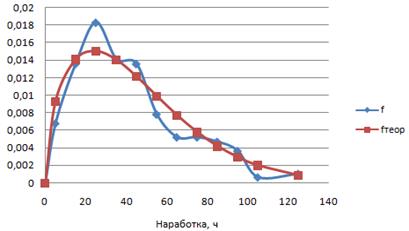
Рисунок 1 - Функция плотности распределения вероятности f(t),наработки турбобура

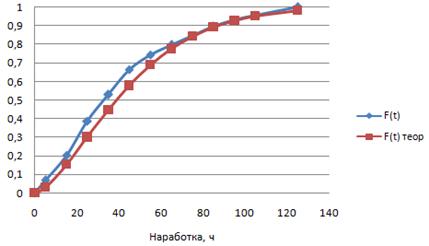
Рисунок 2 - Интегральная функция распределения вероятности F(t), наработки турбобура

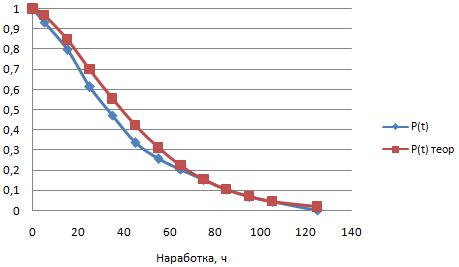
Рисунок 3 – Вероятность безотказной работы

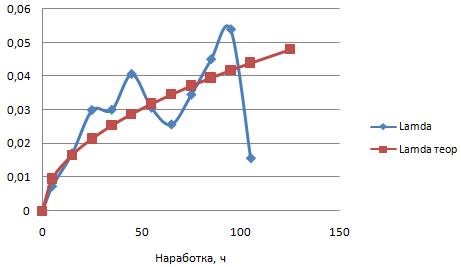
Рисунок 4 - Функция интенсивности распределения вероятностей показателей надежности

2.2 Проверка гипотезы о соответствии эмпирического и теоретического распределения

Критерии согласия применяются для оценки близости статистического и теоретического распределений.

Критерий согласия Пирсона или “критерий “ определяют по следующей формуле [ 2 ] .

где k - число интервалов статистического ряда ;

n_i - частота в i - ом интервале ;

n - общее число значений случайной величины ;

p_i - теоретическая вероятность попадания случайной величины

в i - й интервал .

Вероятность попадания в i - й интервал равна приращению функции вероятности в этом интервале:

p_i =p_in -p_ik

где p_in и p_ik - функция вероятности в конце и начале i- го интервала.

Рассчитав значение , по табл.9 приложения в зависимости от числа степеней свободы определяют вероятность совпадения эмпирического и теоретического распределения. Если найденная вероятность p>0,05, то считают, что статистические данные не противоречат принятому теоретическому распределению. При вероятности совпадения меньше, чем 0,05 считается, что следует подыскать более подходящий закон распределения.

Число степеней свободы равно

r=k-s

где k - число интервалов;

s - число обязательных связей .

Для нормального закона распределения Вейбулла s = 3 , поэтому число интервалов статистического ряда при применении критерия К.Пирсона применяют при числе наблюдений. В каждом интервале рекомендуется иметь не менее 5-10 значений случайной величины.

Число степеней свободы равно r=k-s=11-3=8 при r=8 и (табл.9 приложения) вероятность совпадения теоретического и статистического распределения P=0,1, что не отвергает принятую нами гипотезу о распределении наработки турбобура до отказа по закону Вейбулла.

2.3 Определение доверительных интервалов показателя надежности

Доверительные границы указывают, в каких пределах с заданной доверительной вероятностью может изменяться одиночный показатель надежности. Различают двустороннюю и одностороннюю доверительную вероятность.

По ГОСТ 17510 -72 [ 12] рекомендуется применять следующие значения доверительных вероятностей : 0,80 ; 0,90 ; 0,95 ; 0,99 .

Рассеивание показателей надежности определяют при постановке машин в ремонт, оценка остаточного ресурса и т.д.

Доверительные границы рассеивания среднего значения при распределении Вейбулла равны

и

где и коэффициенты, определяемые по табл. 12 и 13 приложения в зависимости от объема информации и доверительной вероятности.

Значения коэффициентов и взяты из табл. 12 и 13 приложения при n=193 и

Относительно небольшой доверительный интервал показателя надежности объясняется большим объемом информации (n=193).

Заключение