Название: Статистика 18

Вид работы: реферат

Рубрика: Маркетинг

Размер файла: 100.72 Kb

Скачать файл: referat.me-213399.docx

Краткое описание работы: Задача №5 Оборот и издержки обращения двадцати шести торговых предприятий за отчетный период составили (тыс. руб.): Магазины, № п/п Оборот Издержки обращения

Статистика 18

Задача №5

Оборот и издержки обращения двадцати шести торговых предприятий за отчетный период составили (тыс. руб.):

Магазины, № п/п	Оборот	Издержки обращения	Магазины, № п/п	Оборот	Издержки обращения
1	4010	878	14	980	246
2	5305	1010	15	5500	1045
3	3720	740	16	3470	729
4	950	233	17	5008	951
5	2430	588	18	6950	1251
6	3992	838	19	1440	360
7	2903	653	20	5590	1060
8	4902	1029	21	3704	775
9	5404	973	22	2325	553
10	3940	788	23	2635	580
11	4010	862	24	3990	854
12	5307	991	25	5740	1081
13	2870	654	26	3610	784

Для выявления зависимости между размером оборота и издержками обращения произведите группировку магазинов по размеру оборота, образовав четыре группы магазинов с равными интервалами. В каждой группе и в целом подсчитайте:

1) число магазинов;

2) размер оборота – всего и в среднем на один магазин;

3) издержки обращения – всего и в среднем на один магазин;

4) уровень издержек обращения .

Решение оформите в разработочной и групповой таблицах. Сделайте выводы, укажите вид группировки.

Решение:

Определим величину интервала каждой группы по формуле:

, n=4

Составим таблицу для интервалов

№ группы	1	2	3	4
Интервал	950-2450	2450-3950	3950-5450	5450-6950

Сформируем разработочную таблицу

№ группы	Группы магазинов по обороту	№ магазина в списке	Оборот, тыс. руб.	Издержки обращения, тыс. руб.
4	950	233
1	950-2450	5	2430	588
14	980	246
19	1440	360
22	2325	553
Итого по гр.1	5	8125	1980
3	3720	740
7	2903	653
10	3940	788
2	2450-3950	13	2870	654
16	3470	729
21	3704	775
23	2635	580
26	3610	784
Итого по гр.2	8	26852	5703
1	4010	878
2	5305	1010
6	3992	838
3	3950-5450	8	4902	1029
9	5404	973
11	4010	862
12	5307	991
17	5008	951
24	3990	854
Итого по гр.3	9	41928	8386
15	5500	1045
4	5450-6950	18	6950	1251
20	5590	1060
25	5740	1081
Итого по гр.4	4	23780	4437
Всего		26	100685	20506

На основе разработочной группировочной таблицы составим итоговую аналитическую таблицу

№ группы	Группы магазинов	Число магазинов	Оборот, тыс .руб.		Издержки обращения, тыс. руб.		Уровень издержек обращения, %
			Всего	в среднем на 1 магазин	Всего	в среднем на 1 магазин
1	950-2450	5	8125	1625	1980	396	24,4
2	2450-3950	8	26852	3356,5	5703	712,875	21,2
3	3950-5450	9	41928	4658,67	8386	931,78	20
4	5450-6950	4	23780	5945	4437	1109,25	18,7
Итого	26	100685	3872,5	20506	788,69	20,4

Выводы: группировка показала наличие зависимости издержек обращения в зависимости от оборота – с ростом оборота растут издержки обращения, а также направление этой зависимости ‑ с ростом значений факторного признака также растут значения результативного признака.

Задача №10

Предприятие закупило у акционерного общества шерсть для переработки:

Вид шерсти	Выход чистой шерсти, %		Количество шерсти, кг
	фактический	стандартный
Тонкая Полутонкая Полугрубая Грубая	40 38 42 60	35 39 41 58	600 260 400 1700

Определите по каждому виду и в целом:

1) количество стандартной шерсти;

2) долю каждого вида в общем объеме закупленной шерсти;

3) темп роста закупок, если в прошлом периоде закупили у акционерного общества 3050 кг.

Решение:

1) Для определения количества стандартной шерсти по каждому виду шерсти рассчитаем коэффициент пересчета для каждого вида шерсти, а затем умножим его на количество закупленной шерсти. Результаты расчетов занесем в таблицу.

Вид шерсти	Выход чистой шерсти, %		Количество шерсти, кг	Коэффициент пересчета	Количество стандартной шерсти, кг
	фактический	стандартный
Тонкая	40	35	600	1,143	685,714
Полутонкая	38	39	260	0,974	253,333
Полугрубая	42	41	400	1,024	409,756
Грубая	60	58	1700	1,034	1758,621

Тогда общий объем в условно-натуральных единицах составит

685,714+253,333+409,756+1758,621=3107,424 кг

2) Доля каждого вида закупленной шерсти находится как отношение каждого вида шерсти к общему ее количеству, выраженное в процентах. Расчеты проведем в таблице:

Вид шерсти	Количество стандартной шерсти
	кг	%
Тонкая	685,714	22,07
Полутонкая	253,333	8,15
Полугрубая	409,756	13,19
Грубая	1758,621	56,59

3) Рассчитаем темп роста закупок:

, т.е. объем закупок в текущем году увеличился на 1,88%.

Задача №20

Сведения о ценах и количестве проданного товара А по данным регистрации цен на рынке города:

Цена за 1 кг, руб.				Продано кг за
22.06	22.07	22.08	22.09		июль	август	сентябрь
10	14	12	12		3000	3500	3200

Определите:

1) среднемесячные цены за июль, август, сентябрь;

2) среднеквартальную цену товара А.

Решение:

Определим средние цены по формуле средней арифметической простой:

за июль: руб.

за август: руб.

за сентябрь: руб.

Средняя цена за квартал вычисляется по формуле средней арифметической взвешенной:

руб.

Задача №23

С целью изучения вариации размеров торговой площади магазинов произведено 5%-ное выборочное обследование по методу случайного бесповторного отбора. Результаты обследования представлены следующими данными:

Группы магазинов по торговой площади, кв. м	Число магазинов
До 40	2
40-60	4
60-100	9
100-200	10
Свыше 200	5
Итого	30

Определите:

1) средний размер торговой площади одного магазина;

2) дисперсию и среднее квадратическое отклонение;

3) коэффициент вариации;

4) с вероятностью 0,997 предельную ошибку выборки, а также интервал, в котором находится средний размер торговой площади всех магазинов.

Сделайте выводы.

Решение:

Для проведения расчетов нужно преобразовать интервальный ряд в дискретный. Центр интервала определяем по формуле средней арифметической простой. Величины первого и последнего открытых интервалов условно примем равными величинам второго и предпоследнего интервалов соответственно. Результаты вычислений запишем в таблицу:

Группы магазинов по торговой площади, м2	Число магазинов f	Среднее значение интервала, x	x×f	x2 ×f
до 40	2	30	60	1800
40-60	4	50	200	10000
60-100	9	80	720	57600
100-200	10	150	1500	225000
свыше 200	5	250	1250	312500
Итого	30	3730	606900

1. Рассчитаем среднее значение торговой площади по формуле средней арифметической взвешенной

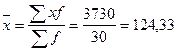м²

2. Рассчитаем дисперсию

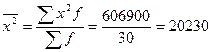
Среднее квадратическое отклонение равно м²

3. Рассчитаем коэффициент вариации:

4. Предельная ошибка для генеральной средней в случае бесповторного отбора вычисляется по формуле:

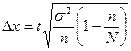, где s² - дисперсия, n - объем выборки, N - объем генеральной совокупности, а t – коэффициент доверия, зависящий от вероятности, с которой делается утверждение (при P=0,997 t=3).

Т.к. выборка 5%-ная, то отношение . Подставим известные данные в формулу:

Пределы для генеральной средней задаются неравенствами:

Таким образом, интервал, в котором находится средний стаж работы всех работников предприятия, будет

124,33 – 36,88 £ a £ 124,33 + 36,88

87,45 £ a £ 161,21

Выводы: колеблемость торговой площади, определяемая коэффициентом вариации, значительна (более 50%). С вероятностью 0,997 можно утверждать, что средняя торговая площадь всей генеральной совокупности лежит в пределах от 87,45 до 161,21 м² .

Задача №32

Производство хлеба и хлебобулочных изделий в области характеризуется следующими данными:

Год	Произведено хлеба, тыс. т
1	166,6
2	141,0
3	128,9
4	121,2
5	120,0

Определите:

1) вид динамического ряда;

2) средний уровень динамического ряда;

3) абсолютные приросты, темпы роста и прироста цепные и базисные, абсолютное содержание 1% прироста;

4) средний абсолютный прирост, средний темп роста и прироста уровней динамического ряда.

Результаты расчетов представьте в таблице. Изобразите динамичес-кий ряд на графике. Сделайте выводы.

Решение:

1) динамический ряд – интервальный, т.к. уровни ряжа приведены за определенный промежуток времени (в данном случае, за год);

2) т.к. данный ряд интервальный, то средний уровень вычисляем по формуле средней арифметической

тыс. тонн

3) рассчитаем абсолютные приросты, темпы роста и прироста, а также абсолютное содержание 1% прироста. Результаты расчетов удобно поместить в таблицу

Год	Произведено хлеба, тыс. т.	Абсолютный прирост		Темп роста		Темп прироста		Абсолютное содержание 1% прироста
		цепной	базисный	цепной	базисный	цепной	базисный
1	166,6
2	141	-25,6	-25,6	84,63%	84,63%	-15,37%	-15,37%	1,666
3	128,9	-12,1	-37,7	91,42%	77,37%	-8,58%	-22,63%	1,41
4	121,2	-7,7	-45,4	94,03%	72,75%	-5,97%	-27,25%	1,289
5	120	-1,2	-46,6	99,01%	72,03%	-0,99%	-27,97%	1,212

Для расчета были использованы следующие формулы:

а) цепные показатели

Dy (ц.с.)=y_i -y_{i -1}

Т_р (ц.с.)=

Т_пр (ц.с.)=Т_р (ц.с.) – 100

б) базисные показатели

Dy(б.с.)=y_i -y₀

Т_р (б.с.)=

Т_пр (б.с.)=Т_р (б.с.) – 100

- абсолютное содержание одного процента прироста

4) рассчитаем средние показатели ряда

Средний абсолютный прирост

Средний темп роста

Средний темп прироста

Изобразим динамический ряд на графике

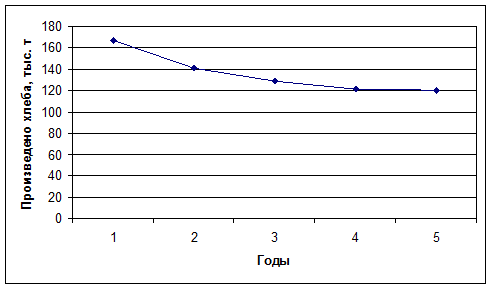
Выводы: динамический ряд является строго убывающим, о чем свидетельствуют все отрицательные цепные абсолютные приросты. Таким образом, объем производства хлеба и х/б изделий области неуклонно снижался. При этом среднегодовое значение производства хлеба составило 135,54 тыс. тонн. Ежегодное снижение производства хлеба составило в среднем 11,64 тыс. тонн, среднегодовой темп роста составил 92,12%, т.е. уровни ряда ежегодно уменьшались в среднем на 7,88%.

Задача №48

Реализация яблок за два периода составила:

Сорт яблок	Продано, кг		Цена 1 кг, руб.
	базисный период	отчетный период	базисный период	отчетный период
А	100	120	35	30
В	210	260	28	22

Определите:

1) индивидуальные индексы цен и физического объема продаж;

2) общий индекс цен;

3) общий индекс физического объема продаж;

4) общий индекс оборота в действующих ценах;

5) абсолютную сумму прироста оборота – всего, в том числе за счет изменения цен и количества проданных товаров.

Сделайте выводы.

Решение:

1) Индивидуальные индексы рассчитываются как отношение величин в отчетном и базисном периоде: , .

Для расчетов общих индексов заполним вспомогательную таблицу

Сорт яблок	Продано, кг		Цена 1 кг, руб.		Индивидуальные индексы		p1 q1	p0 q0	p0 q1
	базисный период	отчетный период	базисный период	отчетный период	физического объема	цен
А	100	120	35	30	1,200	0,857	3600	3500	4200
Б	210	260	28	22	1,238	0,786	5720	5880	7280
Итого	310	380	9320	9380	11480

2) Общий индекс цен Пааше

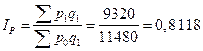или 81,18%

3) Общий индекс физического объема продаж

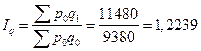или 122,39%

4) Общий индекс оборота в действующих ценах

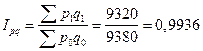или 99,36%

5) абсолютная сумма изменения оборота непродовольственных товаров

руб., в том числе

за счет динамики цен руб.

за счет динамики физического объема руб.

Выводы: в отчетном году оборот от продажи яблок уменьшился на 0,64%. Уменьшение оборота произошло за счет уменьшения цен на 18,82%, но за счет увеличения физического объема продажи оборот увеличился на 22,39%, что в абсолютном выражении составило -60 руб. всего, в том числе за счет уменьшения цен - на -2160 руб. и за счет увеличения физического объема – на +2100 руб.

Задача №46

Продажа безалкогольных напитков предприятием составила (тыс. руб.):

Квартал	Первый год	Второй год	Третий год
1-й	113	106	120
2-й	268	276	292
3-й	454	498	505
4-й	168	187	208

Для анализа сезонности продажи безалкогольных напитков исчислите индексы сезонности. Изобразите сезонную волну графически. Сделайте выводы.

Решение:

Определим средние показатели. Результаты расчетов запишем в таблицу.

Квартал	Первый год	Второй год	Третий год	Итого	Среднее
1	113	106	120	339	113
2	268	276	292	836	278,6667
3	454	498	505	1457	485,6667
4	168	187	208	563	187,6667
Итого	1003	1067	1125	3195	1065
Среднее	250,75	266,75	281,25	798,75	266,25

Теперь можно рассчитать индекс сезонности как отношение ежеквартальных средних значений за 3 года к общему среднему (266,25). Результаты расчетов запишем в таблицу.

Квартал	Индекс сезонности
1	42,44%
2	104,66%
3	182,41%
4	70,49%

Отобразим сезонную волну на графике

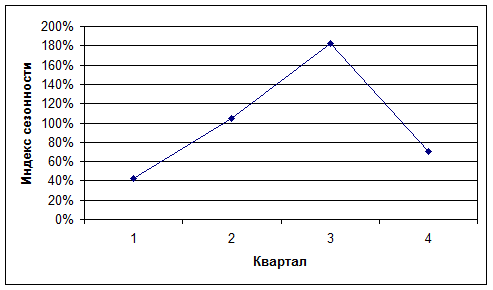
Выводы: на основе расчетов видно, что в первом квартале продажа безалкогольных напитков имеет наименьшее значение (индекс сезонности равен 42,44%), затем она увеличивается и достигает максимума в 3 квартале (индекс сезонности 182,41%). В 4 квартале происходит снижение продаж до 70,49% от среднего уровня продаж.

Задача №65

Данные об обороте и уровне издержек обращения по шести магазинам:

№ торгового предприятия	Оборот, тыс. руб.	Уровень издержек обращения, %
1	207,9	30,1
2	258,3	28,8
3	309,7	25,3
4	340,3	23,5
5	359,4	24,0
6	542,9	22,0

Для изучения зависимости уровня издержек обращения от товарооборота вычислите линейное уравнение связи. Для оценки тесноты связи рассчитайте линейный коэффициент корреляции. Сделайте выводы.

Решение:

Уравнение регрессии, связывающее факторный и результативный показатели, записывается в виде:

,

где a₀ и a₁ - параметры уравнения регрессии, которые находятся из системы двух линейных уравнений

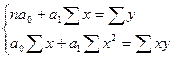
Составим уравнение регрессии. Для этого заполним вспомогательную расчетную таблицу

№ п/п	X	Y	X2	Y2	X×Y
1	207,9	30,1	43222,41	906,01	6257,79	28,72
2	258,3	28,8	66718,89	829,44	7439,04	27,51
3	309,7	25,3	95914,09	640,09	7835,41	26,26
4	340,3	23,5	115804,1	552,25	7997,05	25,52
5	359,4	24	129168,4	576	8625,6	25,06
6	542,9	22	294740,4	484	11943,8	20,62
Итого	2018,5	153,7	745568,3	3987,79	50098,69	153,70

На основе итоговых значений составим систему нормальных уравнений и найдем ее решение:

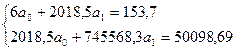
Решая эту систему, получим, что a₁ =-0,024, a₀ =33,75

Таким образом, уравнение регрессии имеет вид: =33,75-0,024x

Используя полученное уравнение, вычислим выравненные значения уровня издержек обращения и занесем их в таблицу.

Рассчитаем линейный коэффициент корреляции r. Для расчета коэффициента корреляции можно воспользоваться следующей формулой:

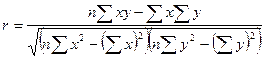
Выводы: т.к. r<0, то линейная связь обратная, т.е. с ростом факторного признака (оборот) результативный признак уменьшается (уровень издержек обращения). Т.к. rÎ[0,7;0,9], то линейная связь сильная.

Найденное значение коэффициента корреляции очень высокое, поэтому найденное уравнение регрессии =33,75-0,024x можно использовать для прогноза уровня издержек обращения при наличии данных об изменении оборота магазина.

Список литературы

1. Практикум по теории статистики: Учеб. пособие для экон. спец. вузов [Р.А. Шмойлова, А.Б. Гусынин, В.Г. Минашкин, Н.А. Садовникова]; Под ред. Р.А. Шмойловой. – М.: Финансы и статистика, 2001.

2. Курс социально-экономической статистики / Под ред. Назарова М.Г. - М.: Финстатинформ, 2002.

3. Общая теория статистики: Учеб. для вузов по направлению и спец. «Статистика» / И.И. Елисеева, М.М. Юзбашев; под ред. И.И. Елисеевой. – 5-е изд., перераб. доп. – М.: Финансы и статистика, 2005.