Название: Анализ статистической совокупности

Вид работы: реферат

Рубрика: Маркетинг

Размер файла: 58.75 Kb

Скачать файл: referat.me-213783.docx

Краткое описание работы: Задача статистического исследования – освоить методику анализа структуры статистической совокупности с использованием компьютерных средств экономико-статистических расчетов, научится использовать аналитические группировки в выявлении взаимосвязей между явлениями.

Анализ статистической совокупности

Задача статистического исследования – освоить методику анализа структуры статистической совокупности с использованием компьютерных средств экономико-статистических расчетов, научится использовать аналитические группировки в выявлении взаимосвязей между явлениями.

В проводимом статистическом исследовании обследованные предприятия выступают как единицы выборочной совокупности, а показатели Среднегодовая стоимость основных производственных фондов и Выпуск продукции – как изучаемые признаки единиц.

Таблица П1

Исходные данные

Порядковый номер единицы наблюдения	Среднегодовая стоимость основных средств, млн руб.	Выручка от продаж продукции, млн руб.
1	94	110
2	107	101
3	134	120
4	158	84
5	163	80
6	167	114
7	173	161
8	173	90
9	177	178
10	179	107
11	200	125
12	201	108
13	205	133
14	237	180
15	212	201
16	213	161
17	214	151
18	216	169
19	218	149
20	230	180
21	234	148
22	237	162
23	241	166
24	169	121
25	45	224
26	276	171
27	290	191
28	298	220
29	167	114
30	205	133
31	330	53
32	260	224

РЕЗУЛЬТАТИВНЫЕ ТАБЛИЦЫ И ГРАФИКИ

Диаграмма 1

Аномальные значения признаков на диаграмме рассеяния

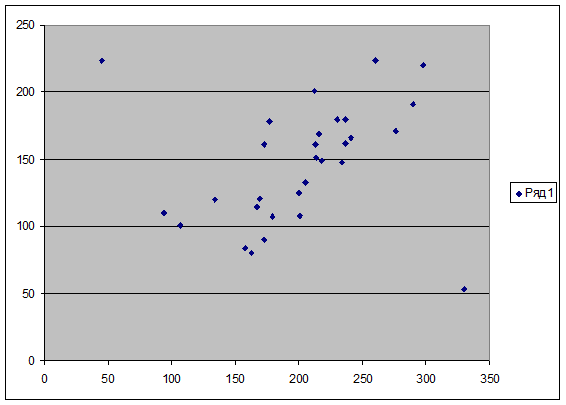
Таблица 2

Аномальные единицы наблюдения

Номер предприятия	Среднегодовая стоимость основных производственных фондов, млн руб.	Выпуск продукции, млн руб.
25	45	224
31	330	53

Таблица 3

Описательные статистики

Среднегодовая стоимость основных средств, млн руб.	Выручка от продаж продукции, млн руб.
Столбец 1	Столбец 2
Среднее	205,3103448	Среднее	146,2758621
Стандартная ошибка	8,273511571	Стандартная ошибка	7,251277542
Медиана	205	Медиана	149
Мода	167	Мода	114
Стандартное отклонение	44,55422334	Стандартное отклонение	39,04932463
Дисперсия выборки	1985,078818	Дисперсия выборки	1524,849754
Эксцесс	0,027595777	Эксцесс	-0,686034479
Асимметричность	0,134309755	Асимметричность	0,15523623
Интервал	191	Интервал	144
Минимум	107	Минимум	80
Максимум	298	Максимум	224
Сумма	5954	Сумма	4242
Счет	29	Счет	29
Уровень надежности(95,4%)	17,2763084	Уровень надежности(95,4%)	15,14173347

Таблица 4,а

Предельные ошибки выборки

Среднегодовая стоимость основных средств, млн руб.	Выручка от продаж продукции, млн руб.
Столбец 2	Столбец 2
Уровень надежности(68,3%)	8,429419969	Уровень надежности(68,3%)	7,387922672

Таблица 4,б

Предельные ошибки выборки

Среднегодовая стоимость основных средств, млн руб.	Выручка от продаж продукции, млн руб.
Столбец 1	Столбец 2
Уровень надежности(99,7%)	26,88832532	Уровень надежности(99,7%)	23,56613728

Таблица 5

Выборочные показатели вариации и асимметрии

Среднегодовая стоимость основных средств, млн руб.	Выручка от продаж продукции, млн руб.
Стандартное отклонение	47,4549611	Стандартное отклонение	38,28309752
Дисперсия	2251,973333	Дисперсия	1465,595556
Среднее линейное отклонение	37,36	Среднее линейное отклонение	32,72888889
Коэффициент вариации, %	23,1137701	Коэффициент вариации, %	26,17184885
Коэффициент асимметрии	0,807299046	Коэффициент асимметрии	0,843083872

Таблица 6

Выходная таблица инструмента ГИСТОГРАММА

Карман	Частота
1
134,8	2
175,6	7
216,4	10
257,2	6
298	4

Таблица 7

Интервальный ряд распределения предприятий по стоимости основных производственных фондов

Группы предприятий по среднесписочной численности работников, чел.	Число предприятий в группе	Накопительная частотность группы
94 - 134,8	3	10,00%
134,8 - 175,6	7	33,33%
175,6 - 216,4	10	66,67%
216,4 - 257,2	6	86,67%
257,2 - 298	4	100,00%
Итого	0	100,00%

Диаграмма 2

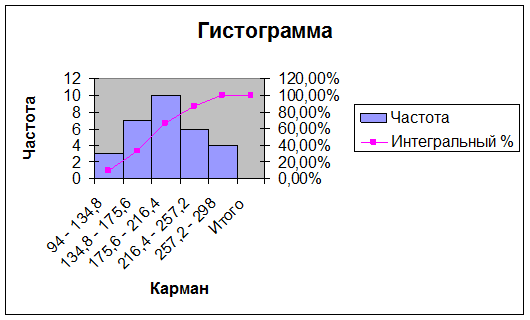
Анализ выборочной совокупности.

Задача 1.

На построенной диаграмме рассеяния (см. Диаграмма 1) визуально видно наличие аномальных точек. Это предприятие №25 (среднегодовая стоимость основных производственных фондов – 45 млн руб.; выпуск продукции – 224 млн руб.) и предприятие №31 (среднегодовая стоимость основных производственных фондов – 330 млн руб.; выпуск продукции – 53 млн руб.). Исключим аномальные единицы наблюдения из первичных данных. Внесем аномальные единицы наблюдения в таблицу 2.

Задача 2.

На основе имеющихся данных составим таблицу

Таблица 8

Описательные статистики выборочной совокупности

Среднегодовая стоимость основных производственных фондов, млн руб.	Выпуск продукции, млн руб.
Столбец1	Столбец2
Среднее, Ч̃	199,6333333	Среднее, Ч̃	143,1666667
Медиана, Me	205	Медиана, Me	148,5
Мода,Mo	167	Мода,Mo	114
Интервал, R	204	Интервал, R	140
Стандартное отклонение, σn	46,04815113	Стандартное отклонение, σn	34,06179026
Дисперсия, σn 2	2120,432222	Дисперсия, σn 2	1160,205556
Среднее линейное отклонение, d	35,44	Среднее линейное отклонение, d	28,42222222
Коэффициент вариации, %, Vσ	23,0663639	Коэффициент вариации, %, Vσ	23,79170449
Коэффициент асимметрии, AsП	0,708678471	Коэффициент асимметрии, AsП	0,856286955

В таблицу внесены обобщающие статистические показатели совокупности, исчисляемые на основе анализа вариационных рядов распределения

Задача 3.

3,а. Если величина V_σ удовлетворяет условию0%<V_σ ≤40%, то степень колеблемости незначительна. В данной совокупности выполняется это условие.

0%<23,0663639≤40%

0%<23,79170449≤40%

3,б. Совокупность является количественно однородной по тому или иному признаку, когда выполняется неравенство V_σ ≤33%. Коэффициенты вариации по каждому признаку удовлетворяют данному условию. Следовательно, совокупности являются количественно однородными.

3,в. Если 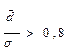, то значения признака неустойчивы. В них имеются «аномальные» выбросы.

Следовательно, несмотря на визуальное обнаружение и исключение нетипичных единиц наблюдения при выполнении задания 1, некоторые аномалии в первичных данных продолжают сохраняться.

Аномалии следует выявить и удалить из выборки.

3,г.

Обобщим данные и составим таблицу

Таблица 9

Распределение значений признака по диапазонам рассеяния признака относительно

Границы диапазонов		Количество значений xi , находящихся в диапазоне
Первый признак	Второй признак	Первый признак	Второй признак
	153,5851822≤xi ≤ 245,6814844	109,1048764≤xi ≤177,228457	23/76,7%	21/65,6%
	107,537031≤xi ≤ 291,7296356	75,04308618≤xi ≤211,2902472	28/87,5%	29/90,6%
	61,48887991≤xi ≤ 337,7777867	40,98129592≤xi ≤245,3520375	31/96,9%	32/100%

Согласно вероятностной теореме П.Л. Чебышева, следует ожидать, что независимо от формы распределения 75% значений признака будут находиться в диапазоне (), а 89% значений – в диапазоне ()

В нормально распределенных и близких к ним рядах вероятные оценки диапазонов рассеяния значений признака таковы:

- 68,3% войдет в диапазон ()

- 95,4% попадет в диапазон () (1)

- 99,7% появится в диапазоне ()

Соотношение (1) известно как правило «трех сигм».

В нашем случае значения каждого из признаков отлично от правила «трех сигм». Значения второго признака ближе к правилу.

Задача 4.

4,а. Размах вариации R= Х _max -Х _min . R для первого признака – 204 млн руб., для второго – 140 млн руб.. Размах вариации устанавливает предельное значение амплитуды колебаний признака.

Среднее линейное отклонение по первому признаку равно 35,44, по второму - 28,42222222. В условиях симметричного и нормального, а также близких к ним распределениям между показателями σ и d имеет место равенство: d ≈ 0,8 σ.

Первый признак: d ≈ 0,8*46,04815113 ≈ 36,838520904.

Второй признак: d ≈ 0,8*34,06179026 ≈ 27,249432208

Рассчитанные по формуле значения приблизительно равны значениям, рассчитанным с помощью программы MSExcel.

Дисперсия σ _n ² оценивает средний квадрат отклонений (). Величина σ очень чутко реагирует на вариацию признака (за счет возведения отклонений в квадрат) и органически вписывается в аппарат математической статистики (дисперсионный, корреляционный анализ и др.). Дисперсия первого признака (2120,432222) более, чем в 1,5 раза превосходит значение дисперсии второго признака (1160,205556).

Среднее квадратическое отклонение σ показывает, насколько в среднем отклоняются индивидуальные значения признака х_i от их средней величины . Так, индивидуальные значения первого признака отличаются от на 46,04815113 млн руб., а второго – на 34,06179026 млн руб..

4,б. Совокупность является количественно однородной по тому или иному признаку, когда выполняется неравенство Vσ≤33%. Коэффициенты вариации по каждому признаку удовлетворяют данному условию. Следовательно, совокупности являются количественно однородными.

4,в. Для оценки надежности (типичности) средней величины х можно воспользоваться значением показателя вариации V_σ . Если его значение невелико, т.е. <40% (как в нашем случае), то индивидуальные значения признака х_i мало отличаются друг от друга, единицы наблюдения количественно однородны и, следовательно, средняя арифметическая величина является надежной характеристикой данной совокупности.

4,г. Если As<0, то асимметрия левосторонняя, если As>0, то асимметрия правосторонняя. И для первого (0,708678471), и для второго (0,856286955) признака асимметрия левосторонняя.

│As│>0,5. Следовательно, асимметрия существенная.

Задача 5.

Интервальный вариационный ряд распределения единиц совокупности по признаку представлен в таблице 7. Гистограмма и кумулята интервального ряда распределения предприятий изображены на Диаграмме 2.

Для полученного интервального ряда значение моды рассчитывается по формуле:

млн руб.

Значение моды в таблице 3 – Мо=167 млн руб..

Для несгруппированных данных мода - это значение признака с наибольшей частотой появления. В интервальном ряду вычисление моды весьма условно. Поэтому между ними могут быть различия.

Анализ генеральной совокупности.

Задача 1.

На основе имеющихся данных составим таблицу

Таблица 10

Описательные статистики генеральной совокупности

Среднегодовая стоимость основных производственных фондов, млн руб.	Выпуск продукции, млн руб.
Столбец1	Столбец2
Стандартное отклонение, σN	46,83535603	Стандартное отклонение, σN	34,64408526
Дисперсия выборки, σN 2	2193,550575	Дисперсия выборки, σN 2	1200,212644
Эксцесс, Ek	0,438466983	Эксцесс, Ek	-0,36007995
Асимметричность, As	-0,03462322	Асимметричность, As	0,085504193

В нашем случае обе дисперсии совпадают.

R_n =204 млн руб.

R_N =6σ_N

R_N =281 млн руб.

Значение размаха вариации различно, поскольку из генеральной совокупности были удалены аномальные значения признаков.

Задача 2.

2, a . Средняя ошибка выборки (µ_Ч̃ ) первого признака - 8,550926996 млн руб., второго - 6,325115661млн руб..

2,б. Предельная ошибка выборки Δ _Ч̃ определяет границы, в пределах которых лежит генеральная средняя . Эти границы задают так называемый доверительный интервал генеральной средней – случайную область значений, которая с вероятностью Р, близкой к 1, гарантированно содержит значение генеральной средней. Эту вероятность называют доверительной вероятностью или уровнем надежности. Наиболее часто используются уровни надежности Р=0,954; Р=0,997; Р=0,683.

В математической статистике доказано, что: Δ _Ч̃ = t * µ_Ч̃ .

Составим таблицу

Таблица 8

Предельные ошибки выборки и ожидаемые границы для генеральных средних

Доверительная вероятность	Коэффициент доверия t	Предельные ошибки выборки		Ожидаемые границы для средних
		для первого признака	для второго признака	для первого признака	для второго признака
0,683	1	8,70660336	6,440269376	190,92672994≤≤208,33993666	136,726397324≤≤149,606936076
0,954	2	17,82706705	13,18667099	181,80626625≤≤217,46040035	129,97999571≤≤156,35333769
0,997	3	27,69995902	20,48964337	171,93337428≤≤227,33329232	122,67702333≤≤163,65631007

Таким образом, предельная ошибка выборки позволяет определить предельные значения показателей генеральной совокупности и их доверительные интервалы.

Задача 3.

Если As<0, то асимметрия левосторонняя, если As>0, то асимметрия правосторонняя. Для первого признака асимметрия левосторонняя (-0,03462322), для второго – правосторонняя (0,085504193).

│As│≤0,25. Следовательно, асимметрия незначительная.

Для первого признака Ek>0. Следовательно, вершина кривой распределения располагается выше вершины нормальной кривой, а форма кривой является более островершинной, чем нормальная. Это говорит о скоплении значений признака в центральной зоне ряда распределения, т.е. о преимущественном появлении в данных значений, близких к средним.

Для второго признака Ek<0. Следовательно, вершина кривой распределения лежит ниже вершины нормальной кривой, а форма кривой более пологая по сравнению с нормальной. Это означает, что значения признака не концентрируются в центральной части ряда, а достаточно равномерно рассеяны по всему диапазону от Х_max до Х_min .

│Ek│ не значителен. Следовательно, кривая распределения незначительно отличается от нормальной.