Интерполяционный многочлен Лагранжа

Лабораторная работа

Выполнил: Евгений

2003 год

Интерполирование и экстраполирование данных.

Многочлен Лагранжа, принимающий заданные значения в узловых точках имеет вид:

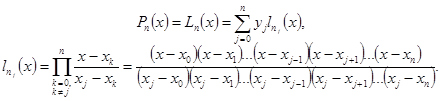
Задание . Восстановить многочлен Лагранжа, удовлетворяющий приведенным исходным данным.

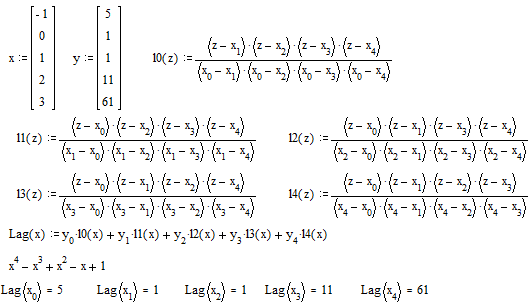Пример:

Варианты:

1).	0	1	2	5
	2	3	12	147
2).	-2	1	2	4
	25	-8	-15	-23
3).	-2	-1	0	1	2
	6	0	2	0	6
4).	0	1	2	5
	3	4	13	148
5).	-2	1	2	4
	26	-7	-14	-22
6).	-2	-1	0	1	2
	5	0	1	0	5
7).	-1	0	1	4
	2	3	12	147
8).	1	2	3	6
	2	3	12	147
9).	-3	0	1	3
	25	-8	-15	-23
10).	-1	2	3	5
	25	-8	-15	-23
11).	-3	-2	-1	0	4
	6	0	2	0	6
12).	-1	0	1	2	3
	6	0	2	0	6
13).	2	3	4	7
	2	3	12	147
14).	-2	-1	0	3
	2	3	12	147
15).	-4	-1	0	2
	25	-8	-15	-23
16).	0	3	4	6
	25	-8	-15	-23
17).	-1	0	1	4
	3	4	13	148
18).	1	2	4	6
	1	2	34	146
19).	-3	0	1	3
	26	-7	-14	-22
20).	-1	2	3	5
	26	-7	-14	-22
21).	-3	-2	-1	0	1
	7	1	3	1	7
22).	-1	0	1	2	3
	5	-1	1	-1	5
23).	-1	0	1	2	3
	2	1	0	1	10
24).	-2	-1	0	1
	1	6	5	4
25).	-3	-2	-1	0
	40	27	12	1
26).	-2	-1	0	1	2
	-27	-4	-1	-6	-7
27).	-1	0	1	2
	-5	-10	-1	34
28).	-2	-1	0	1	2
	16	-1	0	1	8
29).	-2	-1	0	1	2
	-23	-6	1	-2	9
30).	1	2	3	4
	1	2	13	40

Похожие работы

Интерполирование функций
В вычислительной математике существенную роль играет интерполяция функций. Формула Лагранжа. Интерполирование по схеме Эйткена. Интерполяционные формулы Ньютона для равноотстоящих узлов. Формула Ньютона с разделенными разностями. Интерполяция сплайнами.
Математический анализ
Нахождение интерполяционных многочленов Лагранжа и Ньютона, проходящих через четыре точки заданной функции, сравнение их степенных представлений. Решение нелинейного дифференциального уравнения методом Эйлера. Решение систем алгебраических уравнений.
Численные методы
Интерполяционная схема Эйткина. Связь конечных разностей и производных. Распространение ошибки исходных данных при вычислении конечные разности. Свойства разделенной разности. Интерполяционная формула Ньютона для не равноотстоящих узлов. Полином Лагранжа.
Аппроксимация функций
Способы задания функциональных зависимостей: аналитический, графический, табличный; аппроксимирующая функция.
Практическое применение интерполирования гладких функций
Роль интерполяции функций, значения которой совпадают со значениями заданной функции в некотором числе точек. Интерполирование функции полиномами, непосредственно непрерывных функций на отрезке и в точке. Определение понятия погрешности интерполяции.
Интерполирование и приближение функций
Разделенные разности и аппроксимация функций методом наименьших квадратов. Интерполяционные многочлены Лагранжа и Ньютона. Экспериментальные данные функциональной зависимости. Система уравнений для полинома. Графики аппроксимирующих многочленов.
Численные методы 6
ЛЕКЦИЯ №9 МНОГОЧЛЕНЫ ЧЕБЫШЕВА 1. Определение и свойства 2. Интерполяция по Чебышевским узлам 3. Многочлены равномерных приближений 4. Экономизация степенных рядов
Аппроксимация функций 2
ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ РОССИЙСКОЙ ФЕДЕРАЦИИ ОМСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ Кафедра «Авиа- и ракетостроение» Специальность 160801- «Ракетостроение»
Интерполяция функций 2
Министерство образования Российской Федерации. Хабаровский государственный Технический Университет. Кафедра «Прикладная математика и информатика»
Выбор и построение интерполирующей функции
Определение значения заданной функции в указанной точке при помощи интерполяционной схемы Эйткина. Проверка правильности данного решения с помощью кубического сплайна. Практическая реализация данного задания на языке Pascal и при помощи таблиц Excel.