Название: Измерение поверхностного натяжения методом лежащей капли ( газового пузырька)
Вид работы: доклад
Рубрика: Математика
Размер файла: 22.07 Kb
Скачать файл: referat.me-214840.docx
Краткое описание работы: Метод основан на определении диаметра и высоты газового пузырька или капли. Большие размеры пузырька способствуют его деформации в направлении силы земного притяжения.
Измерение поверхностного натяжения методом лежащей капли ( газового пузырька)
.
Метод основан на определении диаметра и высоты газового пузырька или капли. Большие размеры пузырька способствуют его деформации в направлении силы земного притяжения. Помимо этого на деформацию оказывает влияние поверхностное натяжение среды, в которой находится пузырек. Если речь идет о капле, то кривизну поверхности определяет поверхностное натяжение жидкости, составляющей каплю.
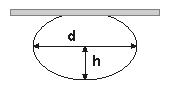 |
Существует одна интересная работа, посвященная выявлению закономерности между деформацией пузырька и поверхностным натяжением: А.Ю.Кошевник, М.М.Кусаков, Н.М.Лубман, ЖФХ, 27, вып. 12, стр. 1887, 1953г. Следуя выводам авторов, можно утверждать, что поверхностное натяжение вычисляется следующим образом (см. рисунок):
= d2 g /H,
где
d - диаметр пузырька;
- плотность исследуемой среды;
g - ускорение свободного падения;
1/H - параметр, зависящий от d/2h. Вычисляется с помощью таблицы.
В сокращенном виде таблица выглядит следующим образом:
| d/2h | 1/H | d/2h | 1/H |
| 1,15 | 0,3304 | 1,6 | 0,06132 |
| 1,2 | 0,2373 | 1,65 | 0,05527 |
| 1,25 | 0,1824 | 1,7 | 0,05018 |
| 1,3 | 0,1466 | 1,75 | 0,04584 |
| 1,35 | 0,1212 | 1,8 | 0,04211 |
| 1,4 | 0,1027 | 1,85 | 0,03886 |
| 1,45 | 0,0885 | 1,9 | 0,03604 |
| 1,5 | 0,07749 | 1,95 | 0,03353 |
| 1,55 | 0,06860 | 2,00 | 0,03132 |
На первый взгляд, достаточно сложно собрать экспериментальную установку для определения поверхностного натяжения. Первое, что приходит в голову - это использовать катетометр, который позволяет определять размеры предмета на расстоянии. Однако, такой прибор очень дорог, особенно в наше время. Возможность использования хорошей фотографической аппаратуры тоже энтузиазма не вызывает.
Мой личный опыт показывает, что можно обойтись более дешевыми средствами. В свое время я занимался фотографированием газовых пузырьков методом экспонирования изображения непосредственно на фотобумагу формата А4. В основе установки был разобранный фильмоскоп, источник света которого освещал кювету с исследуемой жидкостью, а объектив проецировал крупное изображение на экран с фотобумагой. Фокусное расстояние объектива было 78 мм.
Конструкция кюветы была проще некуда: обычная спектрофотометрическая кювета (l=5 см) накрытая покровным стеклом. Под стекло выдувался пузырек воздуха. Кювета стояла в лотке с песком, чтобы ее можно было легко выровнять вдавливанием в песок с помощью пузырькового уровня.
Прежде чем добиться удовлетворительных результатов, мне пришлось преодолеть проблему с калибровкой. Следовало найти необходимый эталон с известными размерами и поместить его точно в то место, где перед этим находился пузырек воздуха. Хорошо подошел в качестве эталона шарик от подшипника. Поскольку он идеально кругл, очень легко подсчитать вертикальную и горизонтальную поправки. Я имею в виду то обстоятельство, что изображение шарика не будет круглым, поскольку экран, на который проецируется изображение, располагается не строго перпендикулярно оптической оси объектива, а поправки позволят вычислять истинные величины высоты и ширины проецируемого объекта.
Проблему с позиционированием шарика и пузырька воздуха я решил тоже просто: над позиционируемым объектом я поместил обычную трубку с диаметром, приблизительно равным диаметру шарика и пузырька. Если глядеть через нее, не приближая глаз к трубке, то можно добиться того, что края трубки и края шарика будут близки. Это значит, что объект можно будет достаточно точно помещать в одно и тоже место. Сами за себя говорят результаты измерений размера шарика:
Результаты измерения изображения шарика диаметром 7,938 мм при температуре 220 С.
| N опыта | высота, мм | ширина, мм |
| 1 | 169,4 | 170,4 |
| 2 | 169,5 | 170,25 |
| 3 | 169,6 | 170,25 |
| среднее | 169,5 | 170,3 |
Несложный расчет показывает, что ошибка операции позиционирования и измерения составляет 0,06%.
Об алгоритме измерения параметров газового пузырька я могу рассказывать долго и с восторгом, но в настоящее время, когда можно без труда найти компьютер со сканером, это никому не интересно.
Скажу одно: в обработке изображений объектов эллиптической формы без компьютера я преуспел. Делал я это с помощью штангенциркуля, прозрачной пленки для эпидиаскопа, швейной иглы и линейки.
Не нужно говорить о том, что для уменьшения ошибки опыты нужно проводить сериями. Каждая серия должна состоять из фотографирования эталона (шарика) и анализируемого объекта (капли или пузырька). Фотографирование должно проводиться на фотобумаге одной партии. После проявления, степень влажности фотобумаги должна быть одинаковой.
Качество обработки изображений было подстать точности позиционирования пузырька воздуха. Результаты экспериментов, проведенных на одном пузырьке, были следующими:
| N опыта | h, мм | d, мм |
| 1 | 78,65 | 252,5 |
| 2 | 78,6 | 252,2 |
| 3 | 78,6 | 252,35 |
| среднее | 78,6 | 252,4 |
*) В каждом опыте пузырек заново позиционировался.
Полученные результаты позволяют надеяться, что можно проводить измерения поверхностного натяжения с точностью 0,1 дин/см.
Только в одном я не преуспел. Я наивно полагал, что покровное стекло, под которое выдувался пузырек, может быть шероховатым (матовым). Шероховатость была нужна для того, чтобы удерживать пузырек на одном месте. Однако оказалось, что шероховатое стекло не позволяет добиться воспроизводимых результатов. По-видимому, следует использовать слабовогнутое стекло, благо это испробовано в ряде работ.
Похожие работы
-
Молекулярно-кинетическая теория
Основные положения теории. Изменение агрегатного состояния вещества. Молекулярно-кинетическая теория идеальных газов. Экспериментальные газовые законы. Температура - мера средней кинетической энергии.
-
Особенности роста пузырька газа в жидкости
Пузырьки газа в жидкости могут расти двумя способами: за счет диффузионного потока через ограничивающую его поверхность, за счет притока частиц к границе из-за конвективных потоков.
-
Просветление тумана в электрическом поле
Приводится теоретическое обоснование возможности просветления тумана в однородном электрическом поле, а так же приводится анализ экспериментов, который позволят определить роль однородного электрического поля в рассеивании тумана.
-
Фигура Земли
Фигура Земли в первом приближении представляет собой эллипсоид вращения, у которого экваториальный радиус (а) больше полярного (b) на 21389 км.
-
Влияние длины полого катода на спектр излучения газового разряда в гелии.
Экспериментально исследовалась интенсивность спектральных линий газового разряда в зависимости от длины полого катода. Рабочий газ - He, давление между электродами ~10-1 Торр. Диаметр полого катода 27мм, диапазон изменения длины полости 0-12 см.
-
Кинетика кипения воды в поле силы тяжести
Эволюция воздушных и паровых пузырьков на дне сосуда. Форма пузырьков. Пузырьки пара. Подъем пузырька с уменьшением радиуса. Измерение шумов, сопровождающих кипение.
-
О некоторых особенностях роста кристаллов NaCl
Об образовании и росте нового типа плавающих кристаллов NaCI и сопутствующих этому явлению эффектах, как-то: образование соляных колец при высыхании капель раствора NaCI, рост дендритов по горизонтальной и вертикальной плоскостям.
-
Спиральные рукава Галактики
Спиральные рукава Галактики играют огромную, как мы видели выше, роль в развитии небесных тел Солнечной системы, поэтому необходимо выяснить вопрос об их происхождении.
-
Алгоритмы сортировки
Проблема упорядочивания данных с практической точки зрения: достоинства и недостатки пяти различных методов сортировки.
-
Условия образования шаровой молнии
Появление шаровой молнии, как правило, связано с грозовой деятельностью протекающей в атмосфере, поэтому прежде чем пытаться понять ее внутреннее строение, необходимо представить те внешние условия, в которых происходит ее образование.