Название: Точные методы решения систем линейных алгебраических уравнений (СЛАУ)
Вид работы: реферат
Рубрика: Математика
Размер файла: 48.74 Kb
Скачать файл: referat.me-215184.docx
Краткое описание работы: Методы решения систем линейных алгебраических уравнений (СЛАУ): Гаусса и Холецкого, их применение к конкретной задаче. Код программы решения перечисленных методов на языке программирования Borland C++ Builder 6. Понятие точного метода решения СЛАУ.
Точные методы решения систем линейных алгебраических уравнений (СЛАУ)
Реферат
на тему:
Точные методы решения систем линейных алгебраических уравнений (СЛАУ)
Введение
Данная лабораторная работа включает в себя два точных метода решения систем линейных алгебраических уравнений (СЛАУ):
Метод Гаусса.
Метод Холецкого.
Также данная лабораторная работа включает в себя: описание метода, применение метода к конкретной задаче (анализ), код программы решения вышеперечисленных методов на языке программирования Borland C++ Builder 6.
Описание метода:
Метод решения СЛАУ называют точным (прямым), если он позволяет получить решение после выполнения конечного числа элементарных операций. К прямым методам относят метод Крамера, метод Гаусса, метод Холецкого и другие. Основным недостатком прямых методов является то, что для нахождения решения необходимо выполнить большое число операций.
Сначала рассмотрим наиболее распространённый метод решения СЛАУ - метод Гаусса, состоящий в последовательном исключении неизвестных.
Пусть дана система уравнений
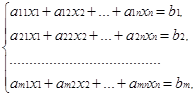(1)
Процесс решения по методу Гаусса состоит из двух этапов. На первом этапе (прямой ход) система приводится к ступенчатому виду:
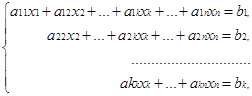
где k
n, aii 
0, i=
, аii - главный элемент системы.
На втором этапе (обратный ход) идет последовательное определение неизвестных из этой ступенчатой системы.
Прямой ход.
Положим а11 0, если а11 = 0, то первым в системе запишем уравнение, в котором а11 0.
Расставим уравнения системы таким образом, чтобы коэффициент при х1 имел наибольшее значение (другими словами отсортируем систему по убыванию).
Преобразуем систему, исключив неизвестное х1 во всех уравнениях, кроме первого (используя элементарные преобразования системы). Для этого умножим обе части первого уравнения на 
и сложим почленно со вторым уравнением системы. Затем умножим обе части первого уравнения на 
и сложим с третьим уравнением системы. Продолжая этот процесс, получаем систему
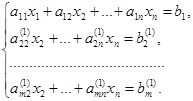
Здесь 
(i, j = 
) - новые значения коэффициентов и правых частей, которые получаются после первого шага.
Аналогичным образом, считая главным элементом 
0, исключим неизвестное х2 из всех уравнений системы, кроме первого и второго, и т.д. Продолжаем этот процесс пока это возможно.
Если в процессе приведения системы (1) к ступенчатому виду появятся нулевые решения (равенства вида 0=0) их отбрасывают. Если же появится уравнение вида 0=bi, а bi 0, то это говорит о несовместимости системы.
Второй этап (обратный ход) заключается в решении ступенчатой системы. В последнем уравнении этой системы выражаем первое неизвестное xk через остальные неизвестные (xk+1, …, xn). Затем подставляем значение xk в предпоследнее уравнение системы и выражаем xk-1 через (xk+1, …, xn), затем находим xk-2, …, x1.
Теперь рассмотрим второй точный метод решения СЛАУ - метод Холецкого (метод квадратных корней).
Он применяется в случае, если матрица системы является симметричной и положительно определенной. В основе метода лежит алгоритм специального LU -разложения матрицы А, где L - нижняя треугольная матрица, а U - верхняя треугольная матрица (если главный минор не равен 0, то существует разложение, причем оно единственно).
Разбиение матрицы А=
на верхнюю и нижнюю к примеру будет выглядеть так
L = 
и U
=
.
В результате преобразований матрица А
приводится к виду A
=
(где 
- транспонированная матрица). Если разложение получено, то решение системы сводится к последовательному решению двух систем с треугольными матрицами: 
и 
. Для нахождения коэффициентов матрицы L
неизвестные коэффициенты матрицы приравнивают соответствующим элементам матрицы A
. Затем последовательно находят требуемые коэффициенты по формулам:
, 
i = 2, 3,..., m,
, 
i = 3, 4,..., m,
, 
i = k+1,..., m,
Применение метода к конкретной задаче (анализ)
Составляя задачи на языке программирования Borland C++ Builder 6 для реализации точных методов решения СЛАУ я учитывал разное количество уравнений в системе (размерность матрицы задавал равным nxn). Но для проверки результатов использовал уравнения
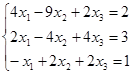(для проверки решения методом Гаусса) (2) и
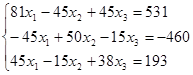(для проверки решения методом Холецкого) (3)
Методы существенно отличаются друг от друга и как описано выше имеют разные подходы для решения СЛАУ. Реализовав методы программным путем и сделав проверки, я пришел к выводу, что не все СЛАУ можно решить методом Холецкого. Как описано выше метод Холецкого применяется для решения систем, которые являются симметричными и положительно определенными. В свою очередь методом Гаусса решаются практически все системы. Исключения составляют невырожденные матрицы, т.е. те матрицы, определитель которых не равен 0.
Листинг программы
#include "Unit1. h"
// ---------------------------------------------------------------------------
#pragma package (smart_init)
#pragma resource "*. dfm"
TForm1 *Form1;
int n=0,l=0;
float r=0,p=0;
const x=100;
float A [x] [x],Ver [x] [x],Nig [x] [x] ;
float *X;
float *Y;
bool fl1=false;
// ---------------------------------------------------------------------------
__fastcall TForm1:: TForm1 (TComponent* Owner)
: TForm (Owner)
{
}
// ---------------------------------------------------------------------------
void __fastcall TForm1:: ButtonOkClick (TObject *Sender)
{
TryStrToInt (Edit1->Text,n);
if (n>1)
{
StringGrid1->Enabled=true;
StringGrid1->RowCount=n;
StringGrid1->ColCount=n+1;
ButtonClear->Enabled=true;
ButtonOk->Enabled=false;
StringGrid1->Color=clWindow;
ButtonGauss->Enabled=true;
ButtonHolec->Enabled=true;
X=new float [n] ;
for (int i=0; i<n; i++)
{
for (int j=0; j<n+1; j++)
{
A [i] [j] =NULL;
}
X [i] =NULL;
}
}
else
{
ShowMessage ("Число должно быть вещественного типа!");
}
}
// ---------------------------------------------------------------------------
void __fastcall TForm1:: ButtonClearClick (TObject *Sender)
{
StringGrid1->Enabled=false;
StringGrid1->RowCount=0;
StringGrid1->ColCount=0;
ButtonClear->Enabled=false;
ButtonOk->Enabled=true;
StringGrid1->Color=clBtnFace;
ButtonGauss->Enabled=false;
}
// ---------------------------------------------------------------------------
void __fastcall TForm1:: ButtonGaussClick (TObject *Sender)
{
Memo1->Lines->Clear ();
for (int i=0; i<n; i++)
{
for (int j=0; j<n+1; j++)
{
TryStrToFloat (StringGrid1->Cells [j] [i],A [i] [j]);
}
}
for (int i=0; i<n; i++)
{
for (int j=0; j<n+1; j++)
{
if (A [i] [j] ==NULL)
{
ShowMessage ("Ошибка! Есть пустые ячейки!");
fl1=true;
i=n;
break;
}
}
}
Memo1->Lines->Add (" МЕТОД ГАУССА: ");
Memo1->Lines->Add ("");
if (! fl1) {
Memo1->Lines->Add ("Матрица приводится к ступенчатому виду: ");
l=0;
for (int i=0; i<n; i++)
{
for (int j=n-1; j>i; j--)
{
if (A [j-1] [l] <A [j] [l])
{
for (int k=0; k<n+1; k++)
{
r=A [j] [k] ;
A [j] [k] =A [j-1] [k] ;
A [j-1] [k] =r;
}
l=0;
}
else
{
if (A [j-1] [l] ==A [j] [l])
{
l++;
j++;
}
if (l==n+1)
{
j--;
l=0;
}
}
}
}
for (int k=0; k<n; k++)
{
for (int i=k; i<n; i++)
{
r=A [i] [k] ;
for (int j=k; j<n+1; j++)
{
A [i] [j] =A [i] [j] /r;
}
}
for (int i=k+1; i<n; i++)
{
for (int j=k; j<n+1; j++)
{
A [i] [j] =A [i] [j] -A [k] [j] ;
}
}
}
X [n-1] =A [n-1] [n] /A [n-1] [n-1] ;
for (int i=n-2; i>=0; i--)
{
r=A [i] [n] ;
for (int j=i+1; j<=n-1; j++)
r=r-A [i] [j] *X [j] ;
X [i] =r/A [i] [i] ;
}
String s="";
for (int i=0; i<n; i++)
{
s="";
for (int j=0; j<n+1; j++)
{
s+=FloatToStr (A [i] [j]) +" ";
}
Memo1->Lines->Add (s);
}
Memo1->Lines->Add ("");
Memo1->Lines->Add ("Корни СЛАУ равны: ");
for (int i=0; i<n; i++)
{
if (X [i] ! =NULL)
{
Memo1->Lines->Add ("x"+IntToStr (i+1) +" = "+FloatToStr (X [i]));
}
else
{
Memo1->Lines->Add ("Нет корней!");
break;
}
}
}
}
// ---------------------------------------------------------------------------
void __fastcall TForm1:: ButtonExitClick (TObject *Sender)
{
Close ();
}
// ---------------------------------------------------------------------------
void __fastcall TForm1:: RadioButton2Click (TObject *Sender)
{
ButtonGauss->Visible=false;
ButtonHolec->Visible=true;
}
// ---------------------------------------------------------------------------
void __fastcall TForm1:: RadioButton1Click (TObject *Sender)
{
ButtonGauss->Visible=true;
ButtonHolec->Visible=false;
}
// ---------------------------------------------------------------------------
void __fastcall TForm1:: ButtonHolecClick (TObject *Sender)
{
Memo1->Lines->Clear ();
for (int i=0; i<n; i++)
{
for (int j=0; j<n+1; j++)
{
TryStrToFloat (StringGrid1->Cells [j] [i],A [i] [j]);
}
}
for (int i=0; i<n; i++)
{
for (int j=0; j<n+1; j++)
{
if (A [i] [j] ==NULL)
{
ShowMessage ("Ошибка! Есть пустые ячейки!");
fl1=true;
i=n;
break;
}
}
}
Memo1->Lines->Add (" МЕТОД ХОЛЕЦКОГО: ");
Memo1->Lines->Add ("");
if (! fl1) {
Y=new float [n] ;
for (int i=0; i<n; i++)
{
Nig [i] [0] =A [i] [0] ;
Ver [0] [i] =A [0] [i] /Nig [0] [0] ;
}
for (int i=0; i<n; i++)
{
for (int j=0; j<n; j++)
{
if (i<j)
{
Nig [i] [j] =0;
}
if (i>j)
{
Ver [i] [j] =0;
}
}
}
for (int i=1; i<n; i++)
{
Ver [i] [i] =1;
}
for (int i=1; i<n; i++)
{
for (int j=i; j<n; j++)
{
for (int k=0; k<i; k++)
{
p=p+Nig [j] [k] *Ver [k] [i] ;
}
Nig [j] [i] =A [j] [i] -p;
p=0;
}
for (int j=i+1; j<n; j++)
{
for (int k=0; k<i; k++)
{
p=p+Nig [i] [k] *Ver [k] [j] ;
}
Ver [i] [j] =1/Nig [i] [i] * (A [i] [j] -p);
p=0;
}
}
for (int i=0; i<n; i++)
{
p=0;
for (int j=0; j<i; j++)
{
p=p+Nig [i] [j] *Y [j] ;
}
Y [i] = (A [i] [n] -p) /Nig [i] [i] ;
}
for (int i=n-1; i>=0; i--)
{
p=0;
for (int j=n-1; j>i; j--)
{
p=p+Ver [i] [j] *X [j] ;
}
X [i] = (Y [i] -p) /Ver [i] [i] ;
}
String s="";
Memo1->Lines->Add ("Нижняя треугольная матрица: ");
for (int i=0; i<n; i++)
{
s="";
for (int j=0; j<n+1; j++)
{
s+=FloatToStr (Nig [i] [j]) +" ";
}
Memo1->Lines->Add (s);
}
Memo1->Lines->Add ("Верхняя треугольная матрица: ");
for (int i=0; i<n; i++)
{
s="";
for (int j=0; j<n+1; j++)
{
s+=FloatToStr (Ver [i] [j]) +" ";
}
Memo1->Lines->Add (s);
}
Memo1->Lines->Add ("");
Memo1->Lines->Add ("Корни СЛАУ равны: ");
for (int i=0; i<n; i++)
{
if (X [i] ! =NULL)
{
Memo1->Lines->Add ("x"+IntToStr (i+1) +" = "+FloatToStr (X [i]));
}
else
{
Memo1->Lines->Add ("Нет корней!");
break;
}
}
}
}
// ---------------------------------------------------------------------------
Результаты расчета:
| МЕТОД ГАУССА: |
МЕТОД ХОЛЕЦКОГО: |
| На первом этапе матрица приводится к ступенчатому виду: 1 - 2,25 0,5 0,5 0 1 6 4 0 0 1 0,625 На втором этапе вычисляются корни СЛАУ исходя из ступенчатой системы: x1 = 0,75 x2 = 0,25 x3 = 0,625 |
Матрица разбивается на верхнюю и нижнюю треугольные матрицы. Нижняя треугольная матрица: 81 0 0 0 45 24,9999980926514 0 0 45 10,0000019073486 8,99999618530273 0 Верхняя треугольная матрица: 1 - 0,555555582046509 0,555555582046509 0 0 1 0,400000095367432 0 0 0 1 0 Корни СЛАУ равны: x1 = 6 x2 = - 5 x3 = - 4 |
Похожие работы
-
Разработка алгоритма точного решения системы линейных уравнений методом Гаусса
АСТРАХАНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ----------------------------------- Факультет информатика Кафедра математики и информатики КУРСОВАЯ РАБОТА
-
Решение систем линейных алгебраических уравнений 2
Нижегородский Технический Университет Институт Радиотехники и Информационных Технологий Кафедра «Прикладная Математика и Информатика» Отчёт по лабораторной работе №2
-
Метод Гаусса для решения систем линейных уравнений
Понятие и специфические черты системы линейных алгебраических уравнений. Механизм и этапы решения системы линейных алгебраических уравнений. Сущность метода исключения Гаусса, примеры решения СЛАУ данным методом. Преимущества и недостатки метода Гаусса.
-
Матричная форма формулы Крамера
С.К. Соболев Матричный способ решения СЛАУ, формулы Крамера, свойство присоединенной матрицы и основное свойство линейной зависимости. Рассмотрим
-
Метод релаксации переменных решения СЛАУ
Методы решения систем линейных уравнений. Метод Якоби в матричной записи. Достоинство итерационного метода верхних релаксаций, вычислительные погрешности. Метод блочной релаксации. Разбор метода релаксаций в системах линейных уравнений на примере.
-
Метод вращений решения СЛАУ
Математические модели явлений или процессов. Сходимость метода простой итерации. Апостериорная оценка погрешности. Метод вращений линейных систем. Контроль точности и приближенного решения в рамках прямого метода. Метод релаксации и метод Гаусса.
-
Метод квадратных корней для симметричной матрицы при решении систем линейных алгебраических уравнений
Исследование метода квадратных корней для симметричной матрицы как одного из методов решения систем линейных алгебраических уравнений. Анализ различных параметров матрицы и их влияния на точность решения: мерность, обусловленность и разряженность.
-
Итерационные методы решения систем линейных алгебраических уравнений
Сущность итерационного метода решения задачи, оценка его главных преимуществ и недостатков. Разновидности итерационных методов решения систем линейных алгебраических уравнений: Якоби, Хорецкого и верхней релаксации, их отличия и возможности применения.
-
Итерационные методы решения системы линейных алгебраических уравнений
Кафедра: Автоматика и информационные технологии "ИТЕРАЦИОННЫЕ МЕТОДЫ РЕШЕНИЯ СЛАУ" Екатеринбург 2006 РЕШЕНИЕ СИСТЕМЫ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ МЕТОДОМ ПРОСТОЙ ИТЕРАЦИИ
-
Точные методы численного решения систем линейных алгебраических уравнений
Метод главных элементов, расширенная матрица, состоящая из коэффициентов системы и свободных членов. Метод квадратных корней для решения систем с симметричной матрицей коэффициентов. Практическая реализация метода Халецкого: программа на языке Pascal.