Название: Задачи по финансовой математике 3

Вид работы: реферат

Рубрика: Математика

Размер файла: 26.81 Kb

Скачать файл: referat.me-215479.docx

Краткое описание работы: ВАРИАНТ 1. Определить число лет. Необходимых для увеличения первоначального капитала в 5 раз, применяя простые и сложные проценты по ставке 15 % годовых.

Задачи по финансовой математике 3

ВАРИАНТ 1.

1. .

2. Определить число лет. Необходимых для увеличения первоначального капитала в 5 раз, применяя простые и сложные проценты по ставке 15 % годовых.

Сначала определим число лет при начислении простых процентов.

Формула простых процентов:

P_n = P(1+ni), где

P_n – наращенная сумма,

i - ставка процента,

P – изначальная сумма,

n - число периодов начисления.

Составим уравнение.

Первоначальный капитал увеличится в 5 раз, следовательно Pn = 5P

5P = P(1 + n*0,15)

1 + n*0,15 = 5

0,15n = 4

n = 26,6 т.е. примерно через 26,5 лет капитал увеличится в 5 раз при простых процентах.

Формула сложных процентов:

P_t = P(1 + i)^t , где

t - количество периодов наращения,

i - ставка процента,

P – изначальная сумма,

P_t – наращенная сумма.

Первоначальный капитал увеличится в 5 раз, следовательно Pn = 5P

5P = P(1 + 0,15)^t

(1,15)^t = 5

t = 11,5 т.е. через 11,5 лет капитал увеличится в 5 раз при сложных процентах

3. Вексель с обязательством 15 тыс. руб. учитывается банком за 3 месяца до погашения с дисконтом 3 тыс. руб. в пользу банка. Определить величину ставки процента.

Формула расчета дисконта банка:

D = d*S*n, где

d – годовая учетная ставка,

n – срок до даты учета,

S – наращенная сумма.

d = D/ S*n

d = 3 000 / 15 000 * 3/12 = 0,8 т.е. 80 %

Другой способ:

P = S (1 - dt ), где

d – банковский дисконт,

t – временная база,

12 = 15 (1 – d*0,25)

d*0,25 = 0,2

d = 0,8

4. Вексель погашается через 3 года за 5 тыс. руб. Определить дисконтную цену векселя по простым и сложным процентам.

По-видимому, в условии пропущена ставка процентов. Примем ставку процентов за 10% годовых.

Тогда:

P = S(1 - dt)

P = 5 000 (1 – 0,1*5) = 2500 – при простых процентах

P = S (1 - d )ⁿ

P = 5000 (1 – 0,1)⁵ = 2952 – при сложных процентах

5. Допустим, что отцу Федору из романа И.Ильфа и Е. Петрова “ двенадцать стульев” срочно надо выкупить стулья у инженера Бруна. Хотя любезная попадья Катерина Александровна и выслала ему телеграфом в Батум необходимую сумму денег, но, увы, наличных денег для совершения покупки у отца Федора в данный момент нет. А стулья, как он прозорливо считает, в любой момент могут достаться конкурентам – Остапу Бендеру и кисе Воробьянинову. Поэтому он решается взять в местном коммерческом банке кредит на один день в сумме 100000 руб. при трехмесячной ставке 9 %, в надежде на то, что на следующий день он непременно получит высланные попадьей деньги. Какую величину процента должен заплатить отец Федор банку?

Ставка i = 9%*4 = 36% годовых

1 день — срок кредита, т. к., согласно банковской практике, дата выдачи кредита и дата его возврата считаются за один день;

Тогда:

P_n = P(1+ni)

P_n = 100 000 (1 + 0,36*1/360) = 100100 руб. – должен будет вернуть

Размер процентов за операцию:

I = 100100 – 100 000 = 100 руб.

6. Пусть во вклад с капитализацией процентов помещены 10 млн. руб. определить наращение суммы вклада через 2 года, если проценты начисляют ежеквартально из расчета 80 % годовых.

Простые проценты:

P_n = P(1+ni) для простых процентов неважно, сколько раз в год начисляют проценты, поэтому ежеквартальное начисление не учитываем (итоговая сумма будет та же)

P_n = 10 000 000 ( 1 + 2*0,8) = 26000000 руб.

Сложные проценты:

P_t = P(1 + i)^t , процентная ставка за квартал t = 80/4 = 20%

P_t = 10 000 000 (1 + 0,2)^2*4 = 42 998 169,6 руб.

7. По муниципальной облигации номиналом 10 тыс. руб., выпущенной на 2,5 года, предусмотрен следующий порядок начисления процентов: первый год- 60 %, в каждом последующем полугодии ставка повышается на 5 %.

Требуется:

1) определить наращенную стоимость облигации по простой процентной и учетной ставкам;

Наращенная стоимость по простой процентной ставке:

P_n = P(1+ni)

P_n = 10 000 (1+1*0,6 + 0,5*0,65 + 0,5*0,7 + 0,5*0,75) = 26500 руб.

Наращенная стоимость по простой учетной ставке:

S = P/(1-d T )

S1год = 10 000/(1 - 0,6*1) = 25000 руб.

Проценты I 1год = 25 000 – 10 000 = 15 000 руб.

S3полугод = 10 000/(1 - 0,65*0,5) = 14 815 руб. (сумма за 3 полугодие)

I 3полугод = 14 815 – 10 000 = 4 815

S4полугод = 10 000/(1 - 0,7*0,5) = 15385 руб.

I 4полугод = 15385 – 10000 = 5385

S5полугод = 10 000/(1 - 0,75*0,5) = 16 000

I 5полугод = 16 000 – 10 000 = 6000 руб.

Суммарная наращенная стоимость по учетной ставке:

S = 15 000 + 4815 + 5385 + 6000 = 31200 руб.

2) составить план наращения первоначальной стоимости по простым процентам;

Период начисления	Метод: простые проценты	Метод: учетная ставка
1 год	10 000(1 + 1*0,6) = 16000	15 000
1,5 года	10 000(0,5*0,65) + 16000 = 19250	19815
2 года	10 000(0,5*0,7) + 19250 = 22750	25200
2,5 года	10 000(0,5*0,75) + 22750 = 26500	31200

3) рассчитать наращенную стоимость облигации по сложной процентной и учетной ставкам;

При начислении сложных процентов применяется формула

S = P(1+i₁ t₁ )·(1+ i₂ t₂ )·(1+ i₃ t₃ )·(1+ i_n t_n )

S = 10 000 * (1 + 0,6*1)*(1 + 0,65*0,5)*(1 + 0,7*0,5)*(1 + 0,75*0,5) = 39 352 руб.

Сложная учетная ставка:

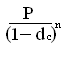
S =

S1год = 10 000 / (1 – 0,6)¹ = 25000 руб.

S3полугод = 25 000 / (1 – 0,65)^0,5 = 42258 руб.

S4полугод = 42258/ (1 – 0,7)^0,5 = 77152 руб.

S5полугод = 77152 / (1 – 0,75)^0,5 = 154304 руб.

4) составить план наращения первоначальной стоимости по сложным процентам;

Период начисления	Метод: сложные проценты	Метод: сложная учетная ставка
1 год	16 000	25000
1,5 года	21200	42258
2 года	28620	77152
2,5 года	39352	154304

5) построить график наращения стоимости по простым и сложным процентам;

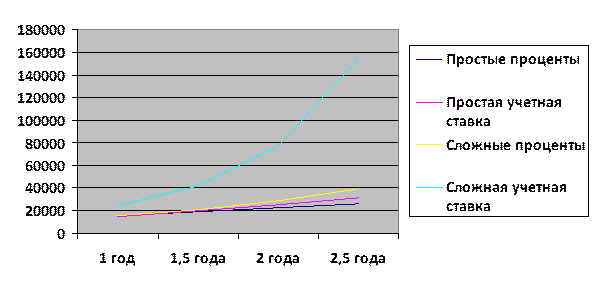
6) проанализировать доходность вариантов наращения стоимости с позиций кредитора и заемщика.

После первого года простая учетная ставка и сложные учетная ставка и проценты дают примерно одинаковый результат, поэтому на этом этапе разницы между этими методами начисления процентов для кредитора и заемщика почти нет. Уже на это этапе резко выделается сложная учетная ставка, которая выгода кредитору и невыгодна заемщику. Разница между методами начисления процентов начинается и усиливается после 1,5 года.

Из графика ясно, что наиболее выгодным для кредитора является вариант сложной учетной ставки. Затем идут сложные проценты, простая учетная ставка и наименее выгодными являются простые проценты.

Для заемщика ситуация противоположна – наиболее выгодным вариантом являются простые проценты, наименее выгодна сложная учетная ставка.

Кредитору выгоднее выдавать ссуду под простой дисконт, а не под простой процент. Простой дисконт (d) представляет собой процентный доход, который вычитается из ссуды в момент ее выдачи. Чтобы убедиться в этом, достаточно сравнить наращенную сумму, которую надо вернуть кредитору при условии выдачи кредита в одинаковой сумме, но под простой процент — в одном случае и под простой дисконт — в другом.