Название: Определение дуальных и двойных чисел

Вид работы: курсовая работа

Рубрика: Математика

Размер файла: 275.39 Kb

Скачать файл: referat.me-215935.docx

Краткое описание работы: Определение операций сложения, вычитания и умножения для дуальных чисел. Определение модуля и сопряжённого числа. Деление на дуальное число. Определение делителя нуля. Запись дуального числа в форме, близкой к тригонометрической форме комплексного числа.

Определение дуальных и двойных чисел

Введение

В настоящее время различные виды комплексных чисел изучаются довольно интенсивно. С учением о комплексных числах связаны важные, не решённые до сегодняшнего дня задачи, над которыми работают учёные во многих странах.

Все системы самых общих комплексных чисел фактически сводятся к следующим трём различным системам: обыкновенные комплексные числа, дуальные числа, двойные числа.

Обыкновенные комплексные числа тесно связаны с вопросом о решении уравнений второй и высших степеней, они играют основную роль в алгебре и во многих разделах математического анализа. Дуальные же и двойные числа не имеют никакого отношения к теории квадратных уравнений с вещественными коэффициентами и вообще сравнительно мало связаны с алгеброй. Основные применения эти числа находят в геометрии (некоторые применения эти системы комплексных чисел находят также в теории чисел).

Основные применения двойных чисел относятся к неевклидовой геометрии Лобачевского и к некоторым другим геометриям, отличным от привычной геометрии Евклида (например, к так называемой псевдоевклидовой геометрии, играющей фундаментальную роль в физической теории относительности).

В нашей работе исследуются дуальные и двойные числа, а также применение этих чисел в геометрии Евклида и в геометрии Лобачевского.

Глава I . Определение дуальных и двойных чисел

1.1 Дуальные числа

Сложение, вычитание и умножение дуальных чисел определяется формулами:

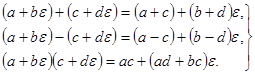(1)

Последняя из этих формул показывает, что произведение дуального числа на другое число будет вещественным лишь в том случае, когда ; если , то последнее равенство можно записать в виде . Вещественным, в частности, является произведение чисел и :

(2)

Число называют сопряжённым числу (и обратно, сопряжено ); корень квадратный из произведения (совпадающий с полусуммой сопряжённых чисел и ) называют модулем дуального числа и обозначают через (отметим, что модуль дуального числа может быть и отрицательным). Сумма двух сопряжённых чисел является вещественной; разность является числом чисто мнимым (т.е. отличается от лишь вещественным множителем). Заметим ещё, что, в полной аналогии с обыкновенными комплексными числами, дуальное число тогда и только тогда совпадает со своим сопряжённым , когда оно является вещественным. Также и справедливые для комплексных чисел формулы (3)

, , , (3)

полностью остаются в силе для дуальных чисел.

Правило деления на дуальное число мы теперь можем записать так:

. (4)

Отсюда видно, что для возможности деления на дуальное число необходимо, чтобы модуль этого числа был отличен от нуля; при этом, в противоположность обыкновенным комплексным числам, дуальное число нулевого модуля само может быть отличным от нуля. В тех случаях, когда невозможность деления на числа нулевого модуля явится для нас затруднением, мы будем считать, что частные и являются числами новой природы, которые условимся обозначать через и ; введём также в рассмотрение всевозможные числа вида , где вещественно. Тогда любое дуальное число будет иметь обратное:

при ; .

Правила действий над символом определяются следующими формулами:

, , , , , (5)

здесь - произвольное число, причём в среднем равенстве , а во втором и в двух последних ( в этих формулах может быть и числом вида ); правила действий над числами определяются так:

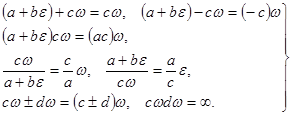(6)

Положим ещё

, ; (6а)

тогда для расширенного (введением чисел , ) множества дуальных чисел сохраняет силу равенство и все правила (3).

Число нулевого модуля можно характеризовать тем, что существует отличное от нуля дуальное число , равное , произведение которого на число равняется нулю:

. (7)

Поэтому эти числа называют делителями нуля.

Дуальные числа ненулевого модуля можно также записать в форме, близкой к тригонометрической форме комплексного числа:

. (8)

Здесь есть модуль числа , а отношение называется аргументом этого числа и обозначается через Arg z (r может быть произвольным вещественным числом, отличным от нуля; - произвольным вещественным числом). Очевидно, что вещественные числа характеризуются равенством нулю их аргумента; сопряжённые дуальные числа и имеют одинаковый модуль r и противоположные аргументы и .

Форма (8) записи дуальных чисел очень удобна в тех случаях, когда эти числа приходится перемножать или делить. Действительно,

; (9)

следовательно, модуль произведения двух дуальных чисел равен произведению модулей сомножителей[1] , а аргумент произведения - сумме аргументов. Отсюда вытекает, что модуль частного двух дуальных чисел равен частному модулей этих чисел, а аргумент частного – разности соответствующих аргументов:

. (10)

Наконец, из этих правил выводятся также и законы, позволяющие возвышать дуальное число в любую степень и извлекать из него корень:

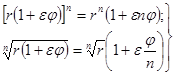(11)

(из последней формулы вытекает, что корень нечётной степени из дуального числа при определяется однозначно; корень же чётной степени не существует, если r <0, и имеет два значения, еслиr >0[2] ).

1.2 Двойные числа

В полной аналогии со всем изложенным выше назовём двойные числа и сопряжёнными, если они имеют вид

и .

Сумма и произведение сопряжённых двойных чисел вещественны; корень квадратный из числа , знак которого совпадает со знаком большего по абсолютной величине из вещественных чисел a и b , называется модулем числа и обозначается через . Легко проверить, что для двойных чисел остаются в силе все формулы (3); кроме того, ясно, что равенство характеризует вещественные числа , а равенство - чисто мнимые числа .

Сложение, вычитание, умножение и деление двойных чисел определяются формулами

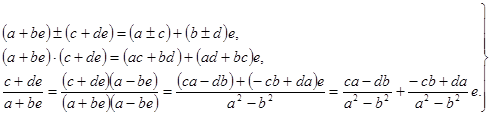(12)

Отсюда следует, что и здесь деление на возможно лишь в тех случаях, когда . Двойные числа , модуль которых равен нулю, называются делителями нуля (заметим, что ). В некоторых случаях оказывается удобным считать частные , и числами новой природы; при этом оказывается необходимым ещё расширить понятие двойного числа, введя дополнительно произведения и новых чисел и на всевозможные вещественные числа c и частные и . Правила действия над символами , , , и определяются формулами (5) и рядом соотношений, родственных (6), например:

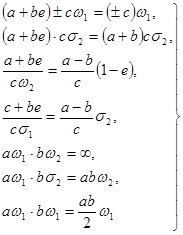(13)

и т. д. Естественно также положить

, , , , (13а)

что обеспечит выполнение для расширенного указанным образом множества двойных чисел равенства и всех соотношений (3).

Двойные числа ненулевого модуля можно также записать в форме, аналогичной форме (8) записи дуальных чисел. Пусть - модуль двойного числа; далее

.

Из определения модуля следует, что и что большая (по абсолютной величине) из дробей и положительна. Отсюда вытекает, что

, или , , (14)

где есть некоторое число (определённое формулами (14)), а и – гиперболический косинус и гиперболический синус аргумента .

Таким образом, имеем

или . (15)

величина называется аргументом двойного числа z и обозначается через Arg z [3] .

Форма (15) записи двойных чисел очень удобна в тех случаях, когда приходится перемножать два или несколько двойных чисел. Действительно, из формул сложения гиперболических функций следует, что

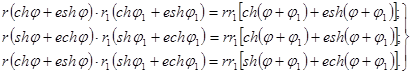(16)

Таким образом, модуль произведения двух двойных чисел равен произведению модулей сомножителей, а аргумент произведения – сумме аргументов; при этом произведение имеет первую или вторую из форм (15) в зависимости от того, имеют ли сомножители одну и ту же или разные формы. Из формул (16) сразу вытекают правила деления двойных чисел:

;

. (17)

Из формул (16) получаются также правила, позволяющие возводить двойное число в любую целую положительную степень n и извлекать из него корень степени n :

,

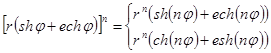
при

n нечётном,

при n чётном;

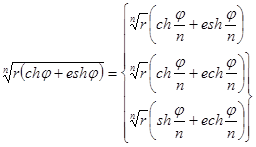
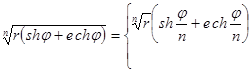
Глава II .

2.1 Дуальные числа как ориентированные прямые плоскости.

Две ориентированные прямые будем называть параллельными лишь в том случае, если они параллельны в обычном смысле и направления этих прямых совпадают (рис. 1, а); параллельные прямые противоположных направлений будем называть противопараллельными (рис. 1, б).

а б

Рис. 1

Под расстоянием от прямой a до не пересекающей её прямой b будем понимать ориентированное расстояние {a , b } от a до b , т.е. ориентированное расстояние от произвольной точки прямой a до прямой b ; очевидно, что {a , b }=- {b , a }, если a иb параллельны, и {a , b }={b , a }, если a и b противопараллельны.

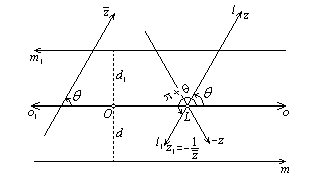
Полярные координаты точек плоскости определяются заданием некоторой точки O (полюса системы координат) и проходящей через O ориентированной прямойo (полярной оси); координатами точки M служат расстояние r = OM этой точки от полюса и угол ={o , m }, образованный с o ориентированной прямой m , соединяющей O иM . Аналогично этому можно определить полярные координаты ориентированных прямых плоскости, для задания которых надо также указать некоторую ориентированную прямую o (полярную ось) и лежащую на o точку O (полюс); координатами прямой l служат угол ={o , l }, образованный l с полярной осью o , и ориентированное расстояние s = {O , L } от O до точки L пересечения l и o (рис. 2,а). Очевидно, что координатаs ориентированной прямой l может иметь любое значение, заключённое между и ; координата – любое значение, заключённое между 0 и 2. Естественно считать, что =0 для прямых, параллельных полярной оси o , и = для прямых, противопараллельных o ; если прямая не пересекает оси o , то координаты s она не имеет (можно считать, что в этом случае ).

Условимся сопоставлять ориентированной прямой l с полярными координатами и s дуальное число

, , (19)

(рис. 2). При этом параллельным o прямым, для которых =0, естественно относить числа нулевого модуля, т.е. делители нуля . Чтобы установить точное соответствие между параллельными o прямыми и делителями нуля, заметим, что расстояние d = {O , l } не параллельной o прямой l от полюса O равно

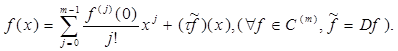(20)

(рис. 2, а). Чтобы формула (20) сохранила силу и для параллельной o прямой m , отстоящей от o на расстоянии {o , m }= d , то этой прямой нужно сопоставить число

(т.е. , где u = 0 и ).

Двум пересекающим o прямым l и l , отличающимся только направлением и, следовательно, имеющим полярные координаты () и (), отвечают дуальные числа

и

.

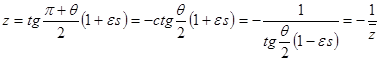Считая, что это соотношение сохраняет силу и для прямых, не пересекающих o , условимся относить противопараллельной o прямой m , отстоящей от o на расстоянии {o , m }=d , число

(заметим, что если расстояние {o , m } от o до параллельной o прямой m , совпадающей по положению на плоскости с прямой m , равно d , то d =- d ). Прямой o , отличающейся только направлением от полярной оси o (противооси), мы сопоставим число .

Тем самым мы устанавливаем полное соответствие между ориентированными прямыми плоскости и дуальными числами, включая сюда также и числа вида w , где w 0 вещественно, и число .

Очевидно, что вещественным числам отвечают проходящие через полюс O прямые; числам модуля 1 – перпендикулярные o прямые; чисто мнимым числам v (числам нулевого модуля) и числам бесконечного модуля w отвечают параллельные и противопараллельные оси o прямые. Сопряжённым числам и отвечают прямые симметричные относительно полюса O ; противоположным числам и – прямые, симметричные относительно полярной оси o (т.е. прямые, пересекающие o в одной и той же точке L и образующие сo равные углы {o , z }={- z , o }; см. рис. 2, б); числам z и отвечают прямые, отличающиеся только направлением. Таким образом, равенства

(а), (б), (в) (21)

можно понимать как записи определённых преобразований в множестве ориентированных прямых плоскости: симметрии относительно точки O , симметрии относительно прямой o и переориентации (изменения направления всех прямых плоскости на противоположное).

Выясним теперь, как записываются с помощью дуальных чисел произвольные движения (к числу которых отнесём и переориентацию, также не меняющую расстояний между точками плоскости).

Параллельный перенос вдоль o на расстояние t переводит прямую, которой отвечает дуальное число

,

в прямую, которой отвечает число

(рис. 3, а). Отсюда вытекает, что этот параллельный перенос можно записать так:

, где , (22)

(т.к. ).

Параллельный перенос на расстояние t в направлении, перпендикулярном o , переводит прямую

в прямую

(рис. 3, б). Но

.

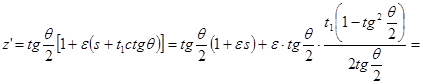
Последнюю формулу можно записать в более изящном виде. Заметим, что

;

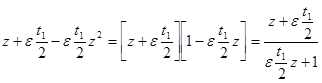таким образом, рассматриваемый параллельный перенос записывается формулой

, где , . (22, а)

Отсюда вытекает, что произвольный параллельный перенос, т.е. перенос на расстояние t в направлении o и на расстояние t в направлении lo , записывается формулой

, , ,

или, если ввести обозначение (т.е. ) и воспользоваться тем, что , , , формулой

, (23)

где , , , .

Перейдём теперь к вращениям плоскости. Очевидно, что поворот вокруг O на угол переводит прямую в прямую , где (рис. 4). Таким образом,

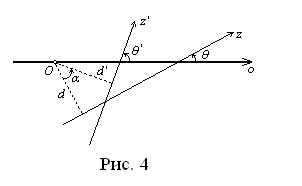
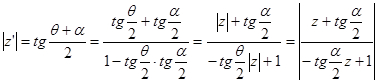(24)

(здесь используется то, что если z иz – дуальные числа, то , и 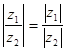). Далее, если d иd ′– расстояния прямых z иz ′ отполюса , то

поэтому

.

С другой стороны, поскольку , то

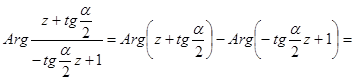
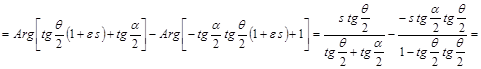
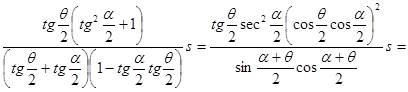
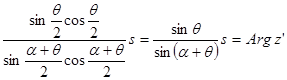. (24а)

Из (24) и (24а) следует, что наше вращение записывается формулой

, (25)

где , .

Наконец, самое общее движение представляет собой поворот (25) вокруг O на некоторый угол , причём это вращение может сопровождаться ещё параллельным переносом (33):

.

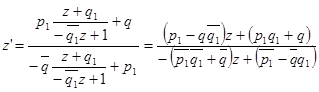В другом виде это преобразование можно записать так:

, (26а)

где , .

Возможно, также, что исходное движение представляет собой симметрию (21б) относительно прямой o , сопровождаемую преобразованием (36а) (вращением вокруг O и параллельным переносом):

. (26б)

Наконец, движение может представлять собой переориентацию (21в), сопровождаемую одним из преобразований (36а) или (36б):

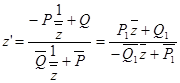, (26в)

где , , или

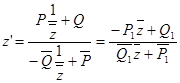, (26г)

где , .

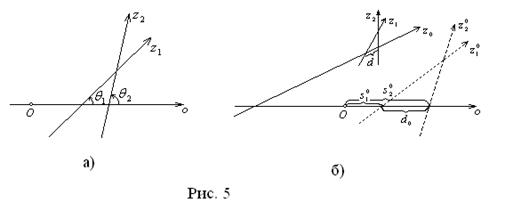
Очевидно, что ориентированный угол {} между прямыми и равен (рис. 5, а)

Это можно записать так:

.

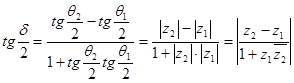Полученный результат можно также представить в следующей симметричной форме:

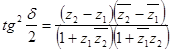. (27)

Найдём теперь ориентированное расстояние d ={[],[]} между точками [] и [] пересечения определённой прямой с двумя другими прямыми и (рис. 5, б). Очевидно, что расстояние d между точками пересечения прямой o с прямыми и равно

.

Пример движения, переводящего данную прямую в прямую o , даётся формулой

;

это движение переводит прямые и в прямые и . Отсюда получаем

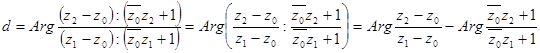.(28)

Условием того, что прямые , и пересекаются в одной точке, является равенство нулю расстояния между точками пересечения и с , т.е., в силу формулы (28), вещественность отношения .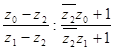

Это условие можно переписать ещё так:

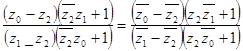. (29)

Следовательно, “уравнение точки”, т.е. условие, которому удовлетворяют прямые , проходящие через одну точку [], имеет вид

,

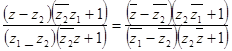или

, A – чисто мнимое (30)

(здесь , ).

Найдём теперь условие того, что четыре ориентированные точки , , и принадлежат одной ориентированной окружности. При этом под ориентированной окружностью мы здесь понимаем совокупность всех ориентированных прямых l , ориентированное расстояние {O , l } которых от данной точки O (центра окружности) имеет фиксированное значение r . Число r называется радиусом окружности; таким образом, радиус ориентированной окружности может быть как положительным, так и отрицательным. Из определения ориентированного расстояния {O , l } от точки O до прямой l следует, что радиус ориентированной окружности будет положительным, если направление обхода противоположно направлению вращения часовой стрелки, и отрицательным в противном случае.

Можно показать, что четыре ориентированные прямые , , и в том и только в том случае принадлежат одной ориентированной окружности или проходят через одну точку, если

{[],[]}{[],[]}={[],[]}{[],[]}. (31)

Чтобы убедиться в этом, рассмотрим рис. 33, на котором изображены четыре ориентированные касательные , , и ориентированной окружности S , касающиеся S соответственно в точках M ,N ,P иQ ; точки [], [], [] и [] обозначены через A , B , C иD . При этом, очевидно, имеем

{A ,B }{C ,D }={A ,P }{P ,B }{C ,Q }{Q ,D }

и

{D ,A }{B ,C }={D ,M }{M ,A }{B ,N }{N ,C }

В силу известного свойства касательных к окружности

{A ,P }={M ,A }, {P ,B }={B ,N }, {C ,Q }={N ,C }, {Q ,D }={D ,M },

значит, во всех случаях выполняется условие (31)

{A ,B }{C ,D }={D ,A }{B ,C }.

Нетрудно убедиться и в том, что если равенство (31) имеет место, то четыре прямые , , и принадлежат одной ориентированной окружности или проходят через одну точку.

Воспользовавшись теперь формулой (28), мы можем переписать условие (31) следующим образом:

,

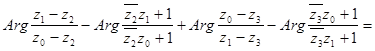
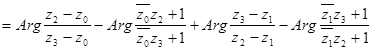или, несколько упростив левую часть последнего равенства и преобразовав правую,

.

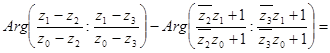
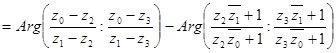Но

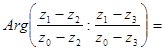
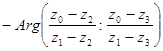
и

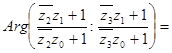
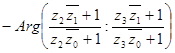
(т.к. 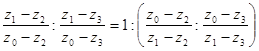и )

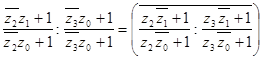Таким образом, равенство (31) можно переписать в следующей простой форме:

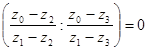. (32)

Дуальное число естественно называть двойным отношением четырёх прямых , , и ; обозначать его будем символом W (,,,). Таким образом, условием того, что четыре прямые , , и принадлежат одной ориентированной окружности (ненулевого радиуса или окружности радиуса нуль – точке), является вещественность двойного отношения W (,,,)= этих четырёх прямых.

Последнему условию можно придать вид:

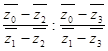=, (33)

откуда вытекает, что уравнение ориентированной окружности (которая в частном случае может оказаться и точкой), определяемой тремя данными прямыми , , и , имеет вид

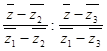=. (34)

Таким образом, уравнение каждой ориентированной окружности (или точки) можно записать в форме (35):

, A иC – чисто мнимые. (35)

Нетрудно проверить, что и, обратно, уравнение (35) всегда выражает окружность (или точку).

Прямую уравнение (35) выражает при

. (36)

2.2 Двойные числа как ориентированные прямые плоскости Лобачевского

В полной аналогии с пунктом 2.1 ориентированным прямым плоскости Лобачевского можно сопоставить двойные числа. А именно, введём, как в пункте 2.1, полярную систему координат для прямых и отнесём каждой пересекающей полярную ось o ориентированной прямой l , имеющей полярные координаты , s , двойное число

, (37)

а расходящейся с o прямой m , направленной в ту же сторону, что и o от их общего перпендикуляра PQ , – число

, (37а)

где d ={m ,o }={P ,Q } – кратчайшее ориентированное расстояние между прямыми m и o , т.е. ориентированное расстояние от o проекции P на прямую m общего перпендикуляра прямых m и o , s ’={O ,Q } – ориентированное расстояние от полюса O системы координат до проекции Q общего перпендикуляра на o (рис. 6).

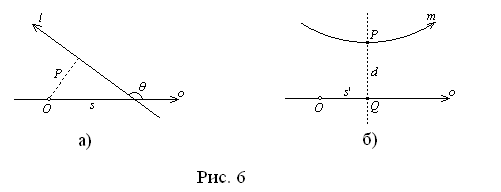
Далее, так как из формулы (37) вытекает, что двум пересекающим o прямым l и l , отличающимся только направлением, соответствуют двойные числа

и

,

то прямой m , отличающейся только направлением ототвечающей числу (37а) расходящейся с o прямой m , сопоставим число

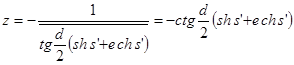. (37б)

Прямые, параллельные оси o , можно рассматривать как предельный случай пересекающих o прямых, отвечающий равенству нулю угла , или как предельный случай расходящихся с o прямых, отвечающий равенству нулю расстояний d . Так как из формул (37) и (37а) следует, что , соответственно , то естественно отнести параллельным o прямым, направленным в ту же сторону, что и o , делители нуля, т.е. числа вида . При этом прямым, параллельным o в положительном или отрицательном направлении, отвечают числа , для которых или , т.к. из (37) и (37а) вытекает, что соотношение равносильно равенству или , а соотношение – равенству или . Из формул неевклидовой тригонометрии следует, что ориентированное расстояние p ={O ,l } от полюса O до пересекающей o прямой l (рис. 6), отвечающей двойному числу , находится из соотношения

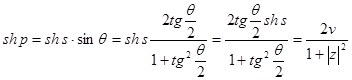. (38)

Поэтому двум параллельным o прямым n иn ' , удалённым от O на расстояние {O , n }={O , n ' }=p , надо отнести числа (где ), для которых , т.е. числа

и .

Наконец, исходя из соотношения , связывающего двойные числа z и z , отвечающие пересекающим ось o или расходящимся с o прямым, отличающимся одна от другой лишь направлением, сопоставим противопараллельным o прямым n и n (т.е. прямым, параллельным o и противоположно направленным), удалённым от O на расстояние {O , n }={O ,n }=p , числа

и ,

где и – числа, обратные делителям нуля: , (если n и n – две прямые, отличающиеся только направлением, то p = {O , n }=–{O , n }=–p ). Полярной оси o и противооси o (т.е. прямой, отличающейся от o только направлением) сопоставим числа 0 и ∞.

Пока у нас не отвечают никаким прямым такие двойные числа z , что (т.к. и ни при каком d ).

Чтобы распространить соответствие между прямыми плоскости Лобачевского и двойными числами на все числа, введём в рассмотрение бесконечно удалённые прямые плоскости Лобачевского, которые можно представить, как касательные к абсолюту модели Клейна (рис. 7). Эти прямые не имеют ориентации.

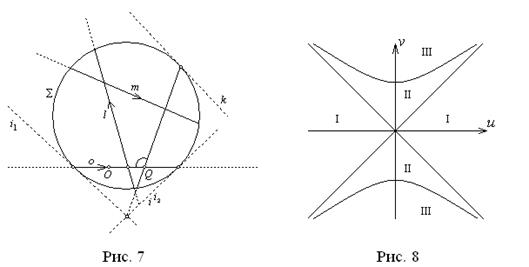
Такая прямая k , не параллельная o (т.е. отличная от касательных к в точках пересечения с o ), характеризуется тем, что d ={k ,o }=; при этом следует считать, что d =, если отвечающая k бесконечно удалённая точка S плоскости Лобачевского расположена справа от o , и d =– в противном случае. Общим перпендикуляром k и o естественно считать прямую SQ , перпендикулярную o ; при этом величина s '= {O ,Q } может принимать любое значение и соответственно этому каждому двойному числу , такому, что , можно сопоставить определённую бесконечно удалённую прямую k . Бесконечно удалённым прямым i и i , параллельным o (рис. 7), сопоставим числа и .

Таким образом, установлено взаимно однозначное соответствие между множеством ориентированных и бесконечно удалённых прямых плоскости Лобачевского и множеством двойных чисел (дополненным числами , , , и ). При этом прямые l , пересекающие полярную ось o , отвечают двойным числам , для которых , т.е. числам, изображаемым на (u ,v )‑плоскости точками области, помеченной на рис. 8 цифрой I. Прямые m , расходящиеся с o и направленные в ту же сторону, что и o , от общего перпендикуляра o и m , отвечают числам z , для которых , т.е. числам, изображаемым на рис. 8 точками области II. Расходящиеся с o прямые m , направленные в противоположную по сравнению с o сторону от общего перпендикуляра m и o , отвечают числам z , для которых , т.е. числам, изображаемым точками области III. Наконец, параллельные o прямые n отвечают числам нулевого модуля, изображаемым двумя прямыми , а противопараллельные o прямые n отвечают числам , (эти числа не имеют изображений на (u ,v )‑плоскости); бесконечно удалённые прямые k отвечают таким числам z , что , т.е. числам, изображаемым точками гиперболы , и ещё двум числам , .

Очевидно, что как и в случае евклидовой плоскости, соотношения

(а), (б), (в) (21)

выражают симметрию относительно точки O , симметрию относительно прямой o и переориентацию (изменение направлений всех прямых на обратное). Произвольные движения, как можно показать, выражаются здесь теми же формулами, что и в евклидовом случае:

, или , или , или ;

только в качестве переменных z ' , z и коэффициентов P , Q здесь фигурируют не дуальные, а двойные числа, в связи с чем следует дополнительно потребовать, чтобы выражение было положительно (если P и Q – дуальные числа, то последнее условие выполняется автоматически, т.к. произведения и не могут быть отрицательны). Также и ориентированный угол {z , z } между прямыми z и z и ориентированное расстояние d ={[z z ],[z z ]} между точками пересечения прямых z и z с прямой z определяются формулами (27) и (28):

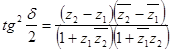, (27)

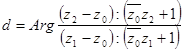. (28)

Из (28) следует, что условием того, что три прямые z , z и z пересекаются в одной точке, является вещественность отношения 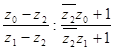. Отсюда вытекает, что уравнение точки неевклидовой геометрии Лобачевского имеет вид

, A – чисто мнимое. (30)

Циклом множества ориентированных и бесконечно удалённых прямых плоскости Лобачевского следует называть:

а)–в) совокупность прямых, касающихся ориентированного цикла, т.е. окружности, предельной линии или эквидистанты;

г) пучок равного наклона, т.е. пучок всех ориентированных прямых, образующих постоянный ориентированный угол с фиксированной осью пучка;

д) параллельный пучок, т.е. пучок всех прямых, параллельных в обоих направлениях фиксированной оси пучка;

е) неориентированную бесконечно удалённую окружность .

При таком понимании термина цикл мы получаем, что необходимым и достаточным условием того, что четыре ориентированные прямые z , z , z и z плоскости Лобачевского принадлежат одному циклу, является вещественность двойного отношения этих четырёх прямых. Отсюда снова вытекает, что уравнение каждого цикла можно записать в форме:

, A иC – чисто мнимые. (35)

Чтобы решить, является ли цикл (35) окружностью, предельной линией, эквидистантой, параллельным пучком или пучком постоянного наклона, надо выяснить, сколько общих прямых имеет этот цикл с бесконечно удалённой окружностью (абсолютом) (т.е. сколько решений имеет система , ) и будет ли вещественным или мнимым угол (27) между двумя соседними прямыми цикла. Воспользовавшись этим, получаем:

цикл (35) является окружностью, если

, (39а)

цикл (35) является предельной линией, если

, , (39б)

является эквидистантой, если

, (39в)

параллельным пучком, если

(39г)

пучком равного наклона, если

(39д)

цикл (35) представляет собой абсолют , если

, (39е)

Точку (обыкновенную, бесконечно удалённую или идеальную) уравнение (35) выражает в том случае, если имеет место соотношение:

. (36)

Заключение

дуальное число модуль сопряженный

В нашей работе мы определили операции сложения, вычитания и умножения для дуальных чисел, дали определение модуля и сопряжённого числа, вывели правило деления на дуальное число, расширив множество дуальных чисел, ввели определение делителя нуля, представили запись дуального числа в форме, близкой к тригонометрической форме комплексного числа, и вывели законы, позволяющие возводить дуальное число в любую целую положительную степень n и извлекать из него корень степени n . Аналогичным образом определили двойные числа и действия над ними. Введя на плоскости полярную систему координат, установили полное соответствие между ориентированными прямыми плоскости и дуальными числами, с помощью дуальных чисел записали все виды движений, нашли условие того, что четыре ориентированные точки принадлежат одной ориентированной окружности, и, пользуясь этим условием, вывели уравнение ориентированной окружности. В полной аналогии с изложенным выше установили взаимно однозначное соответствие между множеством ориентированных и бесконечно удалённых прямых плоскости Лобачевского и множеством двойных чисел и вывели формулы для записи движений. Также мы дали определение цикла множества ориентированных и бесконечно удалённых прямых плоскости Лобачевского и получили необходимое и достаточное условие принадлежности одному циклу четырёх прямых плоскости Лобачевского.

Эти результаты могут быть приложены к доказательству многих теорем евклидовой геометрии и неевклидовой геометрии Лобачевского. При этом использование дуальных и двойных чисел во многом упрощает доказательство различных теорем.

Литература

Яглом И. М. Комплексные числа и их применение в геометрии. – М.: Физматгиз, 1963

Маркушевич А. И. Комплексные числа и конформные отображения. – М.: Наука, 1979

[1] Это утверждение остаётся в силе и в том случае, когда модуль одного или обоих сомножителей равен нулю (т. к. если , то и ; так, например, ).

[2] Нетрудно видеть, что корень целой степени n >1 из дуального числа , модуль которого равен нулю (из числа, являющегося делителем нуля), извлечь нельзя.

[3] В некоторых случаях удобно считать, что аргумент двойных чисел, имеющих вторую из форм (15), является обыкновенным комплексным числом

Arg {r (sh j +ech j )}=j -i.

Это соглашение удобно тем, что в таком случае всегда

z =|z| [ch (Arg z )+esh (Arg z )]