Название: Полином Жегалкина

Вид работы: курсовая работа

Рубрика: Математика

Размер файла: 228.85 Kb

Скачать файл: referat.me-215957.docx

Краткое описание работы: Изучение булевых функций. Алгоритм представления булевых функций в виде полинома Жегалкина. Система функций множества. Алгебраические преобразования, метод неопределенных коэффициентов. Таблица истинности для определенного количества переменных.

Полином Жегалкина

Уфимский государственный авиационный технический университет

Кафедра АПРиС

Курсовая работа

по дискретной математике

«Полином Жегалкина»

Выполнили:

Проверила:

Шерыхалина Н.М.

Уфа – 2008

Оглавление

Цель работы

Введение

Теоретическая часть

Алгоритм

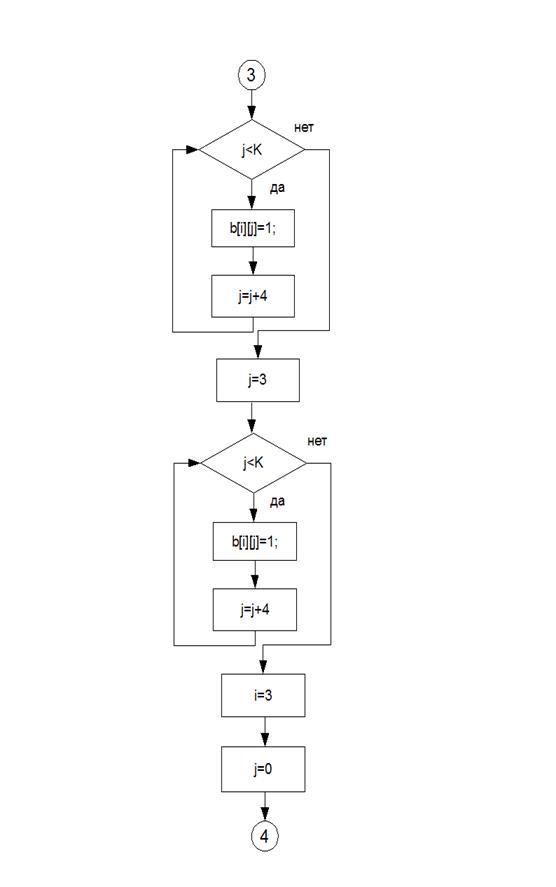
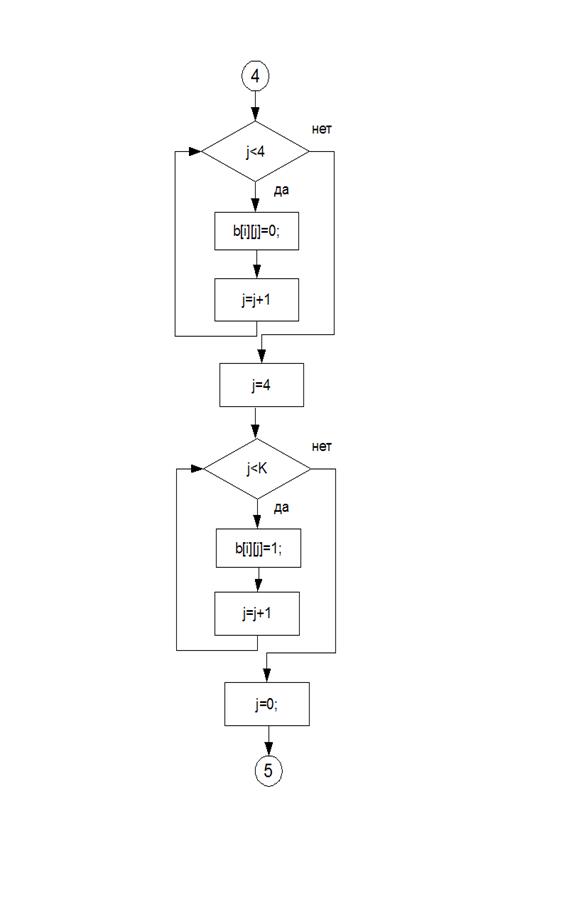
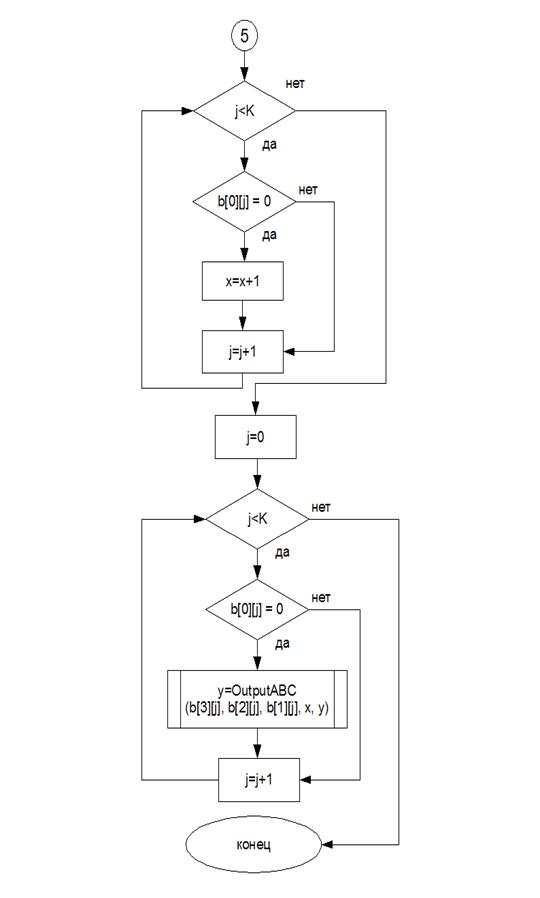
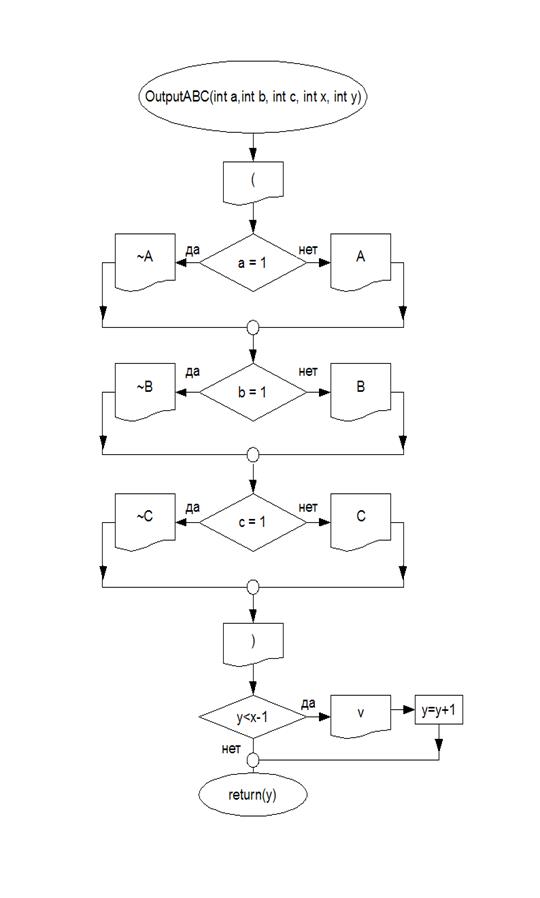
Блок-схемы

Листинг программы

Тестирование программы

Заключение

Список использованной литературы:

Цель работы

Целью данной работы является изучение булевых функций, разработка алгоритма их представления в виде полинома Жегалкина и написания программы, реализующей этот алгоритм.

Введение

В курсе дискретной математики изучаются функции, область определения которых – дискретное множество. Простейшим (но нетривиальным) таким множеством является множество, состоящее из двух элементов.

Теоретическая часть

Полнота и замкнутость

Определение 1:Система функцийиз P2 (множества всех булевых функций) называется функционально полной, если любая булева функция может быть записана в виде формулы через функции этой системы.

Пример:

1) Само множество ;

2);

3) - не полна.

Теорема 1. Пусть даны две системы функций из

, (I)

. (II)

Известно, что система I полная и каждая функция системы I выражается через функции системы II. Тогда система II является полной.

Доказательство: Пусть . В силу полноты системы I , функцию h можно выразить в виде формулы .

По условию теоремы

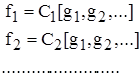
Поэтому

ч. т. д.

Примеры:

1) - полная.

2) - тоже полная, так как .

3) - тоже полная.

4) - тоже полная, так как

,

,

. ((2) – I)

5) - неполная.

Докажем это от противного.

Предположим, что .

Но .

Противоречие.

6) - неполная (сохраняет константу 0).

6’) - полная.

7) - неполная (сохраняет константу 1).

8)

тогда взяв в качестве системы I систему 2) можно заключить, система функций 8) – полная. Тем самым, справедлива

Теорема Жегалкина. Каждая функция из может быть выражена при помощи полинома по модулю 2 – (полинома Жегалкина):

,

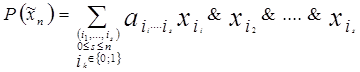где . (1)

Имеем: число разных сочетаний равно числу подмножеств множества из n элементов. Каждое aik может принимать одно из 2-х значений {0,1}. Тогда число разных полиномов Жегалкина равно , т.е. равно числу различных булевых функций.

Т. о. получаем единственность представления функций через полином Жегалкина.

Способы представления функции в виде полинома Жегалкина

1) Алгебраические преобразования

.

Пример:

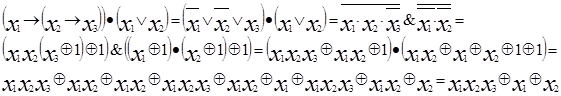
2) Метод неопределенных коэффициентов

- искомый полином Жегалкина (реализующий функцию ).

Вектор из формулы (1) будем называть вектором коэффициентов полинома .

Нам нужно найти неизвестные коэффициенты .

Поступаем так. Для каждого составим уравнение , где - выражение, получаемое из (1) при . Это дает систему из уравнений с неизвестными, она имеет единственное решение. Решив систему, находим коэффициенты полинома .

3) Метод, базирующийся на преобразовании вектора значения функции

Пусть - вектор значений функции.

Разбиваем вектор на двумерные наборы:

.

Операция T определена следующим образом:

.

Применяем операцию Т к двумерным наборам:

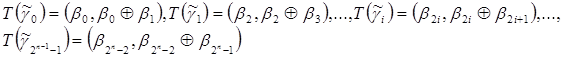
Используя построенные наборы, конструируем четырехмерные наборы, которые получаются в результате применения операции Т к четырехмерным наборам, выделяемым из.

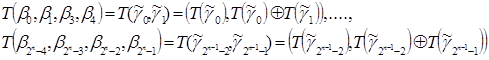
Затем от четырехмерных наборов переходим (аналогично) к восьмимерным и т.д., пока не построим - мерный набор. Он и будет искомым вектором коэффициентов полинома .

Пример:

Пусть вектор значений функций = (0,0,0,1,0,1,1,1)

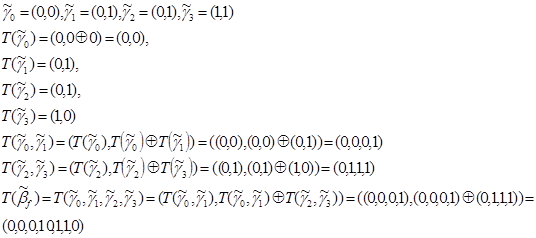
Полученный вектор является искомым векторов коэффициентов полинома .

Определение 2: Пусть M – некоторое подмножество функций из P2. Замыканием M называется множество всех булевых функций, представимых в виде формул через функции множества M. Обозначается [M].

Замечание. Замыкание инвариантно относительно операций введения и удаления фиктивных переменных.

Примеры.

1) M=P2, [M]=P2.

2) M={1,x1Åx2}, [M] – множество L всех линейных функций вида

, (ciÎ{0,1}).

Свойства замыкания:

1) Если М замкнуто, то [M]=M;

2) [[M]]=[M];

3) M1ÍM2 Þ [M1]Í[M2];

4) [M1ÈM2]Ê[M1]È[M1].

Определение 3. Класс (множество) M называется (функционально) замкнутым, если [M]=M.

Примеры.

1) Класс M=P2 функционально замкнут;

2) Класс {1,x1Åx2} не замкнут;

3) Класс L замкнут (линейное выражение, составленное из линейных выражений линейно).

Новое определение полноты. M – полная система, если [M]=P2.

Алгоритм

булевой функция полином жигалкин

В данной программе был реализован метод неопределенных коэффициентов для построения полинома Жегалкина.

1. Получить таблицу истинности для определенного количества переменных;

2. Заполнить значения функции для каждого из наборов таблицы истинности;

3. Последовательно вычислить неизвестные коэффициенты;

4. Записать функцию в виде полинома Жегалкина с вычисленными коэффициентами.

x1	x2	x3	f
0	0	0	f1
0	0	1	f2
0	1	0	f3
0	1	1	f4
1	0	0	f5
1	0	1	f6
1	1	0	f7
1	1	1	f8

.

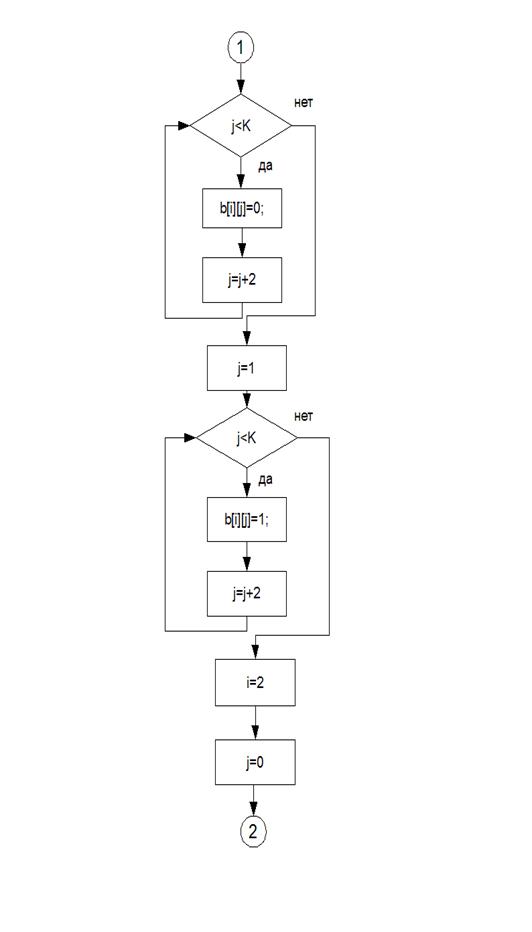
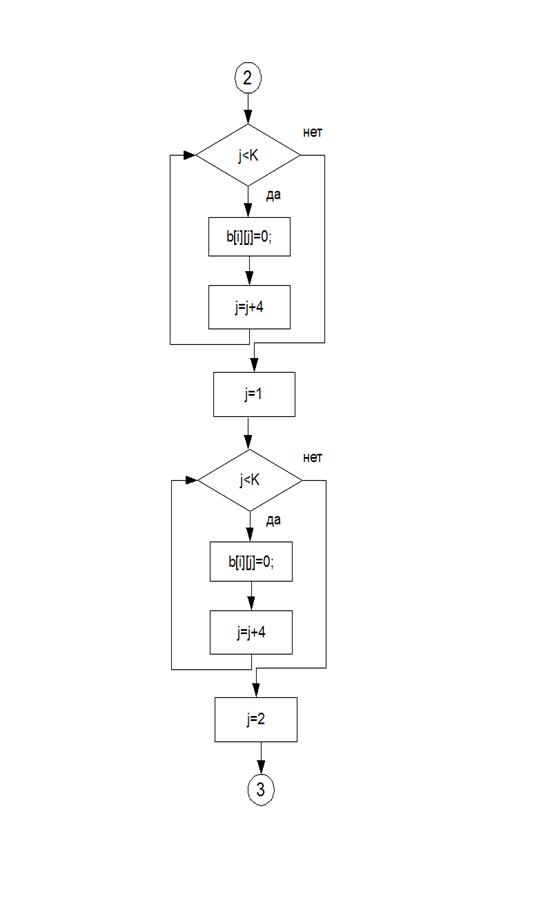
Листингпрограммы:

#include<iostream.h>

#include<conio.h>

int FuncVolume (int &f)

{

do {cout <<"Vvedite znachenit funkcii na dannom nabore :"<<endl;

cin>>f;

if ((f!=0)&&(f!=1))

cout<<"Error!!!Funkciya mojet prinimat' znachenie libo 0 libo 1!n";

}

while ((f!=0)&&(f!=1));

return f;

}

void main()

{

clrscr();

const N=8;

int m[5];

int f[N],a[N];

for (int i =0; i<N; i++)

{

FuncVolume (f[i]);

}

a[0]= f[0];

a[3]=f[0]^f[1];

a[2]=f[0]^f[2];

a[1]=f[0]^f[4];

m[0]=f[1]^a[2]^a[3];

a[5]=m[0]^f[3];

m[1]=f[1]^a[1]^a[3];

a[6]=m[1]^f[5];

m[2]=f[1]^a[1]^a[2];

a[4]=m[2]^f[6];

m[3]=a[3]^a[4]^a[5];

m[4]=m[2]^m[3]^a[6];

a[7]=m[4]^f[7];

cout<<"nnTablica istinnosti dlya dannoy funkcii : nn";

cout<<"x_1 x_2 x_3 fnn";

cout<<" 0 0 0 "<<f[0]

<<"n 0 0 1 "<<f[1]

<<"n 0 1 0 "<<f[2]

<<"n 0 1 1 "<<f[3]

<<"n 1 0 0 "<<f[4]

<<"n 1 0 1 "<<f[5]

<<"n 1 1 0 "<<f[6]

<<"n 1 1 1 "<<f[7]<<"nn";

cout<<"nnZnachenie koefficientov v polimome Jigalkina : nn" ;

for (i=0; i<N;i++)

{

cout<<"a_"<<i<<" "<<a[i]<<"n";}

cout<<"Polinom Jigalkina dlya dannoy funkcii imeet vid : n f = "<<a[0]

<<"^("<<a[1]<<"*x_1)^("<<a[2]<<"*x_2)^("<<a[3]<<"*x_3)^("<<a[4]<<"*x_1*x_2)^n^("<<a[5]<<"*x_2*x_3)^("<<a[6]<<"*x_1*x_3)^("

<<a[7]<<"*x_1*x_2*x_3)";

getch();

}

Тестирование программы:

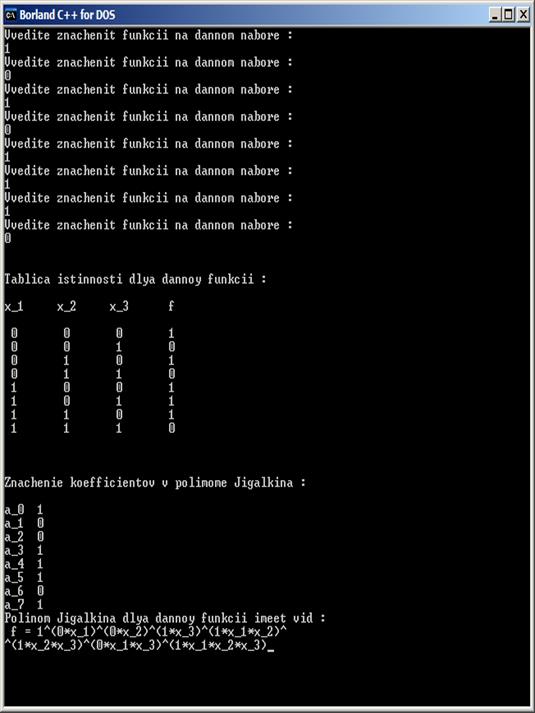
На каждом наборе вводятся единицы, то есть функция является тождественной единицей. Простейшая проверка на правильность работы программы:

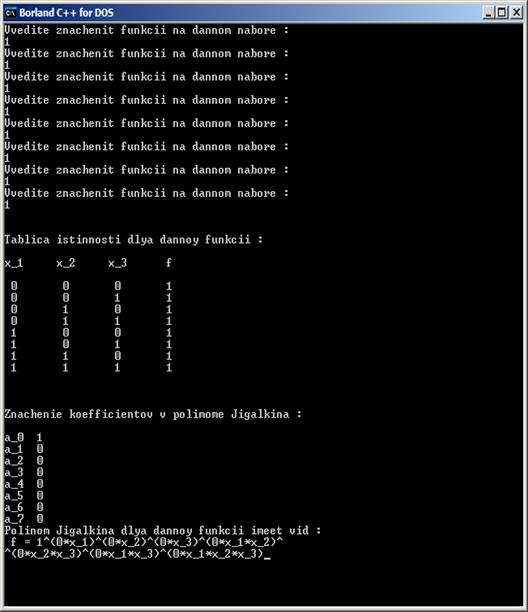
Так же реализована проверка на правильный ввод данных:

Заключение

В курсовой работе был реализован метод неопределенных коэффициентов для представления функции в виде полинома Жегалкина. По данному алгоритму на языке С++ была написана программа, результат которой был продемонстрирован.

Список использованной литературы

1. Яблонский С.В. Введение в дискретную математику. — М.: Наука. — 1986

2. Н.А.Ахметова, З.М.Усманова Дискретная Математика. Функции алгебры логики учебное электронное издание – Уфа – 2004

3. Гаврилов Г. П., Сапоженко А. А. Задачи и упражнения по дискретной математике: Учебное пособие. – 3-е изд., перераб. – М.: ФИЗМАТЛИТ, 2005.