Название: Оптимизация организационных решений

Вид работы: контрольная работа

Рубрика: Математика

Размер файла: 640.31 Kb

Скачать файл: referat.me-216278.docx

Краткое описание работы: КОНТРОЛЬНАЯ РАБОТА по дисциплине « ОПТИМИЗАЦИЯ ОРГАНИЗАЦИОННЫХ РЕШЕНИЙ» Задание №1 Решение задачи об оптимальном направлении капиталовложений в строительную отрасль и оптимизации поставки строительных грузов

Оптимизация организационных решений

КОНТРОЛЬНАЯ РАБОТА

по дисциплине

« ОПТИМИЗАЦИЯ ОРГАНИЗАЦИОННЫХ РЕШЕНИЙ»

Задание №1

Решение задачи об оптимальном направлении капиталовложений в строительную отрасль и оптимизации поставки строительных грузов

Определить наиболее экономичный вариант прироста мощности (строительства или реконструкции) и одновременно рассчитать оптимальный план перевозок строительной продукции до потребителя.

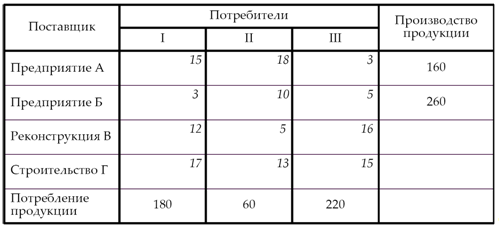
Решение

Составим базисные планы:

а) метод северо-западного угла

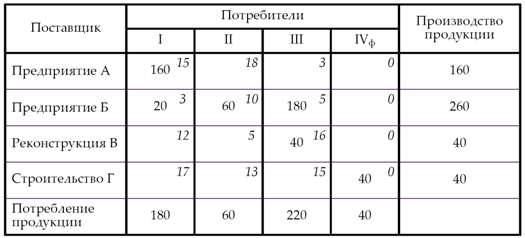
Значение целевой функции:

L₁ = 160 х 15 + 20 х 3 + 60 х 10 + 180 х 5 + 40 х 16 + 40 х 0 =

= 2 400 + 60 + 600 + 900 + 640 + 0 = 4 600 у. е.

б) метод двойного предпочтения

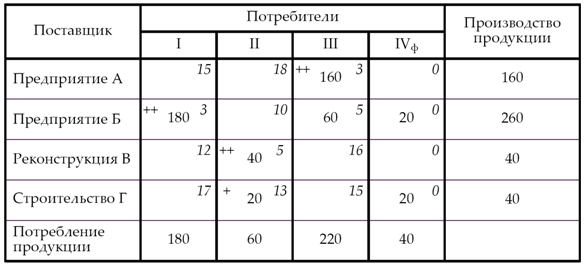
Значение целевой функции:

L₂ = 180 х 3 + 160 х 3 + 60 х 5 + 20 х 0 + 40 х 5 + 20 х 13 + 20 х 0 =

= 540 + 480 + 300 + 0 + 200 + 260 + 0 = 1 780 у. е.

в) метод аппроксимации Фогеля

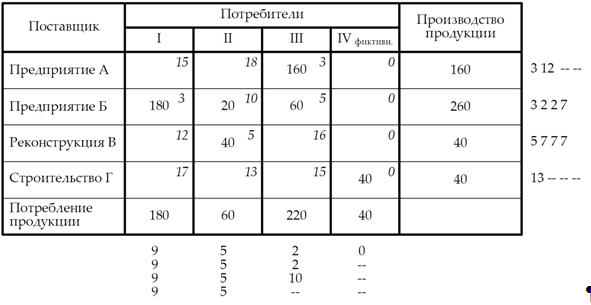
Значение целевой функции:

L₃ = 160 х 3 + 180 х 3 + 20 х 10 + 60 х 5 + 40 х 5 + 40 х 0 =

= 480 + 540 + 200 + 300 + 200 + 0 = 1 720 у. е.

Проведем проверку матрицы на вырождение:

N – число занятых клеток матрицы, N = 6.

N = m + n – 1 = 4 + 4 – 1 = 7.

6 ≠ 7.

Следовательно, матрица – вырожденная, поэтому в одну из свободных ячеек в зоне вырождения вводим условную нулевую поставку груза.

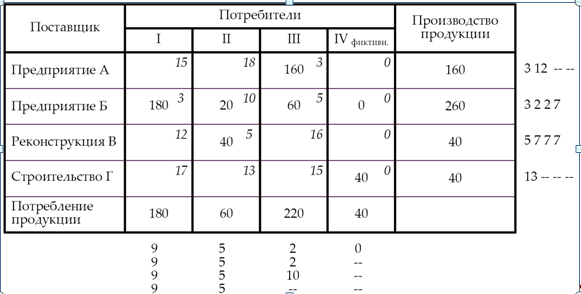
Оптимальный план находим на основании базисного плана, построенного методом аппроксимации Фогеля, так как этот план имеет минимальную целевую функцию.

Проверим матрицу на оптимальность с помощью потенциалов строк u и столбцов v .

Потенциалы определим по занятым клеткам матрицы, тем самым соблюдая условие оптимальности (c_ij = u _ij + v_ij ).

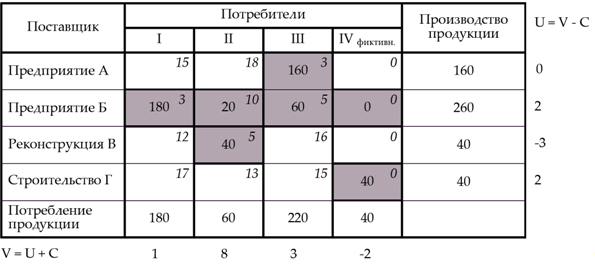
Произведем проверку свободных клеток базисного плана на оптимальность.

Коды свободных клеток	Δ = cij – ( vij + uij )	Примечание
A-I	15 – (1 + 0) = 15	>0
A-II	18 – (8 + 0) = 10	>0
A-IV	0 – (-2 + 0) = 2	>0
B-I	12 – (1 – 3) = 14	>0
B-III	16 – (3 – 3) = 16	>0
B-IV	0 – (-2 + 2) = 0	=0
Г-I	17 – (1 + 2) = 14	>0
Г-II	13 – (8 + 2) = 3	>0
Г-III	15 – (3 + 2) = 10	>0

В данном случае все значения Δ ≥ 0, следовательно, составленный план неоптимален, переходим к улучшенному плану перевозок. В этом случае среди незагруженных клеток, для которых Δ ≥ 0, находим клетку с наибольшей величиной превышения стоимости (B-III).

Строим замкнутый контур, начиная перемещаться из потенциальной клетки.

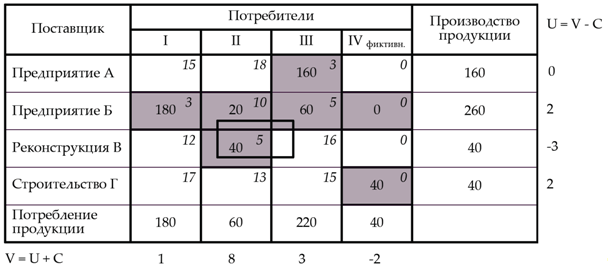
Контур распределения:

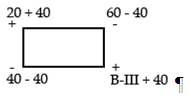
Составим новый план распределения.

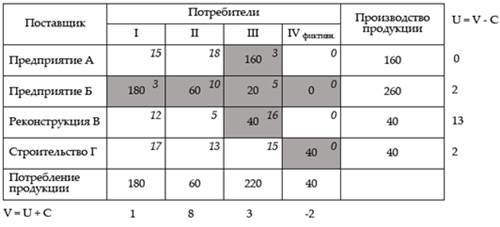
Его целевая функция:

L₄ = 160 х 3 + 180 х 3 + 60 х 10 + 20 х 5 + 40 х 16 + 40 х 0 =

= 480 + 540 + 600 + 100 + 640 + 0 = 2 360 у. е.

Проверяем полученную матрицу на оптимальность.

Коды свободных клеток	Δ = cij – ( vij + uij )	Примечание
A-I	15 – (1 + 0) = 15	>0
A-II	18 – (8 + 0) = 10	>0
A-IV	0 – (-2 + 0) = 2	>0
B-I	12 – (1 – 3) = 14	>0
B-II	5 – (8 + 13) = -16	<0
B-IV	0 – (-2 + 13) = -11	<0
Г-I	17 – (1 + 2) = 14	>0
Г-II	13 – (8 + 2) = 3	>0
Г-III	15 – (3 + 2) = 10	>0

Наибольшее превышение стоимости наблюдаем в клетке А-I.

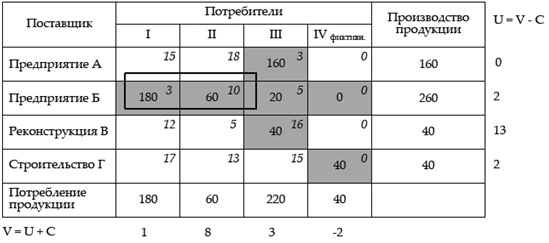
Контур распределения:

Новый план распределения:

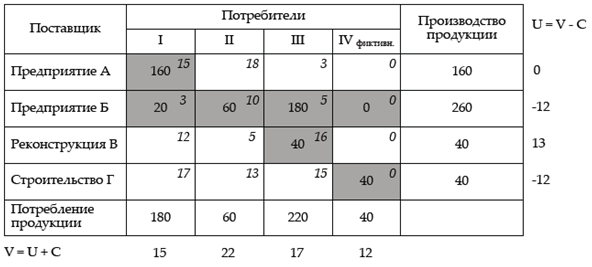
Его целевая функция:

L₄ = 160 х 15 + 20 х 3 + 60 х 10 + 180 х 5 + 40 х 16 + 40 х 0 =

= 2 400 + 60 + 600 + 900 + 640 + 0 = 4 600 у. е.

Проверяем полученную матрицу на оптимальность.

Коды свободных клеток	Δ = cij – ( vij + uij )	Примечание
A-II	18 – (22 + 0) = -4	<0
A-III	3 – (17 + 0) = -14	<0
A-IV	0 – (12 + 0) = -12	<0
B-I	12 – (15 + 13) = -16	<0
B-II	5 – (22 + 13) = -30	<0
B-IV	0 – (12 + 13) = -25	<0
Г-I	17 – (15 - 12) = 14	>0
Г-II	13 – (22 - 12) = 3	>0
Г-III	15 – (17 - 12) = 10	>0

Данный план распределения продукции является наиболее эффективным из представленных, хотя не до конца оптимальным.

Вывод

Поскольку в оптимальном плане прирост мощности 40 тыс. у. е. продукции за счет строительства отнесен на фиктивного потребителя, то строительство нового цеха или пристройку цеха к действующему следует считать нецелесообразным, и капитальные вложения необходимо направить на реконструкцию действующего предприятия.

Задание №2

Применение симплекс-метода для оптимальной организации

ремонтно-строительных работ

Определить максимальное количество квартир в домах кирпичных и крупнопанельных, которые можно отремонтировать из имеющихся ресурсов.

Ресурсы		Потребность в ресурсах на одну квартиру
Наименование	Количество		кирпичный дом	панельный дом
Арматура, т	900		0,6	1,3
Пиломатериалы, м3	520		0,8	0,3
Цемент, т	7 000		5	9
Керамическая плитка, тыс. шт.	400		0,5	--
Трудозатраты, чел. дн.	55 000		70	50

Решение

Для решения данной задачи применим симплекс-метод.

Обозначим:

Х₁ – искомое количество квартир в кирпичном доме;

Х₂ – искомое количество квартир в панельном доме.

Целевая функция:

L = Х₁ + Х₂ max

Ограничениями будут неравенства, полученные на основании исходных данных:

1. Арматура 0,6Х₁ + 1,3 Х₂ ≤ 900 ;

2. Пиломатериалы 0,8Х₁ + 0,3 Х₂ ≤ 520 ;

3. Цемент 5Х₁ + 9Х₂ ≤ 7 000 ;

4. Керамическая плитка 0,5Х₁ ≤ 400 ;

5. Трудозатраты 70Х₁ + 50Х₂ ≤ 55 000 ;

6. Х₁ ≥ 0 ;

7. Х₂ ≥ 0 .

Поскольку имеется только два неизвестных, то применим геометрическое решение. Для удобства построений преобразуем не равенства.

1. 6Х₁ + 13 Х₂ ≤ 9 000 ;

2. 8Х₁ + 3 Х₂ ≤ 5 200 ;

3. 5Х₁ + 9Х₂ ≤ 7 000 ;

4. 5Х₁ ≤ 4 000 ;

5. 7Х₁ + 5Х₂ ≤ 5 500 ;

6. Х₁ ≥ 0 ;

7. Х₂ ≥ 0 .

Геометрически ограничения неравенств выражаются в виде открытых полуплоскостей, ограниченных осями координат и линиями, описываемыми равенствами, полученными из выражений ограничений:

1. 6Х₁ + 13 Х₂ = 9 000 ;

2. 8Х₁ + 3 Х₂ = 5 200 ;

3. 5Х₁ + 9Х₂ = 7 000 ;

4. 5Х₁ = 4 000 ;

5. 7Х₁ + 5Х₂ = 5 500 .

Нанесем эти линии на график.

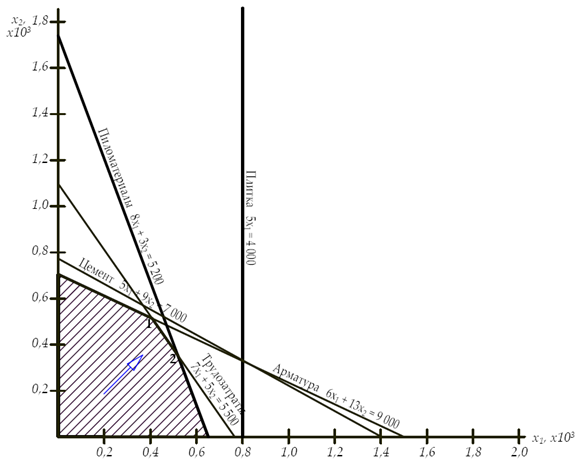
В целом условиям неравенств удовлетворяет заштрихованная область. Оптимальное решение находится на контуре этой фигуры в одной из узловых точек и определяется совместным рассмотрением выражений:

L = Х₁ + Х₂ max

6Х₁ + 13 Х₂ = 9 000 ;

8Х₁ + 3 Х₂ = 5 200 ;

5Х₁ + 9Х₂ = 7 000 ;

5Х₁ = 4 000 ;

7Х₁ + 5Х₂ = 5 500.

Возрастание целевой функции направлено слева вверх под углом 45°, и последней точкой в допустимой области будет точка 1 или 2.

Точка 1 получена пересечением прямых, описываемых равенствами:

6Х₁ + 13 Х₂ = 9 000;

7Х₁ + 5Х₂ = 5 500.

Решая эти равенства, найдем координаты точки 1: Х₁ = 200; Х₂ = 600.

Аналогично найдем координаты точки 2 из выражений:

7Х₁ + 5Х₂ = 5 500;

8Х₁ + 3 Х₂ = 5 200.

Координаты точки 2: Х₁ = 498; Х₂ = 406.

Найдем, какая из указанных точек дает большее значение целевой функции.

L ₁ = Х₁ + Х₂ = 200 + 600 = 800;

L ₂ = Х₁ + Х₂ = 498 + 406 = 904.

Оптимальной является точка 2, дающая 498 квартир в кирпичных домах и 406 в панельных. При этом будут полностью исчерпаны такие ресурсы как пиломатериалы и трудозатраты.

Использование остальных ресурсов найдем, решая вышеуказанные равенства при зафиксированных значениях Х₁ = 498; Х₂ = 406.

0,6 х 498 + 1,3 х 406 = 299 + 528 = 827 (арматура), неиспользовано 73 т арматуры.

5 х 498 + 9 х 406 = 2 490 + 3 654 = 6 144 (цемент), неиспользовано 856 т.

0,5 х 498 = 249 тыс. шт. (керамическая плитка), неиспользовано 151 тыс. шт.

Полученные результаты занесем в таблицу:

Ресурсы		Количество ресурсов
Наименование	в наличии		использованных	неиспользованных
Арматура, т	900		827	73
Пиломатериалы, м3	520		520	-
Цемент, т	7 000		6 144	856
Керамическая плитка, тыс. шт.	400		249	151
Трудозатраты, чел. дн.	55 000		55 000	--

Вывод : Максимальное количество домов, которые можно отремонтировать, используя данные ресурсы – 498 шт. (кирпичные) и 406 шт. (панельные). При ремонте пиломатериалы и трудозатраты используются полностью, остальные ресурсы – с остатком.

Задание №3

Применение методов динамического программирования

(принципа оптимальности Р. Беллмана)

при календарном планировании в строительстве

Выбрать такую очередность включения объектов в строительный поток, чтобы длина суммарного пути перебазирования оказалась минимальной.

Исходные данные – расстояние между пунктами, км

Индекс пунктов (объектов)	А0	А1	А2	А3	А4
А0	0	20	5	10	40
А1	20	0	10	25	30
А2	5	10	0	35	15
А3	10	25	35	0	50
А4	40	30	15	50	0

Составим таблицу вариантов, состоящих лишь из трех участков перебазирования. Сгруппируем эти варианты по одинаковым объектам, стоящим на последнем месте.

Вариант	Суммарное расстояние, км	Вариант	Суммарное расстояние, км
А0 А2 А3 А1 А0 А3 А2 А1	5 + 35 + 25 = 65 10 + 35 + 25 = 70	А0 А1 А2 А3 А0 А2 А1 А3	20 + 10 + 35 = 65 5 + 10 + 25 = 40
А0 А2 А4 А1 А0 А4 А2 А1	5 + 15 + 30 = 50 40 + 15 + 10 = 65	А0 А1 А4 А3 А0 А4 А1 А3	20 + 30 + 50 = 100 40 + 30 + 25 = 95
А0 А3 А4 А1 А0 А4 А3 А1	10 + 50 + 30 = 90 40 + 50 + 25 = 115	А0 А2 А4 А3 А0 А4 А2 А3	5 + 15 + 50 = 70 40 + 15 + 35 = 90
А0 А1 А3 А2 А0 А3 А1 А2	20 + 25 + 35 = 80 10 + 25 + 10 = 45	А0 А1 А2 А4 А0 А2 А1 А4	20 + 10 + 15 = 45 5 + 10 + 30 = 45
А0 А1 А4 А2 А0 А4 А1 А2	20 + 30 + 15 = 65 40 + 30 + 10 = 80	А0 А1 А3 А4 А0 А3 А1 А4	20 + 25 + 50 = 95 10 + 25 + 30 = 65
А0 А3 А4 А2 А0 А4 А3 А2	10 + 50 + 15 = 75 40 + 50 + 35 = 125	А0 А2 А3 А4 А0 А3 А2 А4	5 + 35 + 50 = 90 10 + 35 + 15 = 60

Из каждой пары вариантов выберем наиболее перспективные (с меньшим значением). Затем развиваем и сопоставляем лишь перспективные варианты.

Вариант	Суммарное расстояние, км	Вариант	Суммарное расстояние, км
А0 А2 А3 А1 А4 А0 А2 А4 А1 А3 А0 А3 А4 А1 А2 А0 А3 А1 А2 А4 А0 А1 А4 А2 А3 А0 А3 А4 А2 А1	65 + 30 = 95 50 + 25 = 75 90 + 10 = 100 45 + 15 = 60 65 + 35 = 110 75 + 10 = 85	А0 А2 А1 А3 А4 А0 А4 А1 А3 А2 А0 А2 А4 А3 А1 А0 А2 А1 А4 А3 А0 А3 А1 А4 А2 А0 А3 А2 А4 А1	40 + 50 = 90 95 + 35 = 130 70 + 25 = 95 45 + 50 = 95 65 + 15 = 80 60 + 30 = 90

Составляем таблицу, в которую внесем перспективные варианты из предыдущей таблицы и добавим к каждому из них А₀ (возвращение мехколонны на исходную базу).

Вариант	Суммарное расстояние, км
А0 А2 А4 А1 А3 А0 А0 А3 А1 А2 А4 А0 А0 А3 А4 А2 А1 А0 А0 А3 А1 А4 А2 А0	75 + 10 = 85 60 + 40 = 100 85 + 20 = 105 80 + 5 = 85

Таким образом, устанавливаем, что есть два равноценных оптимальных варианта последовательности строительства объектов.

Задание №4

Оптимизация очередности строительства объектов

в неритмичных потоках

Определить оптимальную очередность строительства нескольких объектов, при которой достигается минимальная общая продолжительность строительства, а также величину общей продолжительности строительства при исходной и оптимальной очередности строительства объектов.

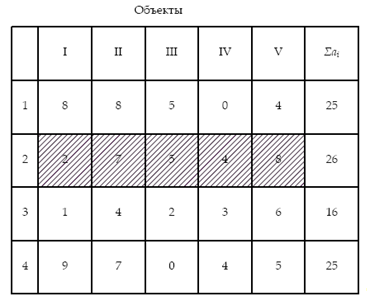
Выделяем поток №3 как поток наибольшей продолжительности. Затем по каждому объекту находим общее рабочее время, предшествующее потоку наибольшей продолжительности и общее рабочее время, последующее за потоком наибольшей продолжительности.

В третью строку под матрицей записываем со своим знаком разницу между продолжительностью работы на данном объекте последней и первой бригад.

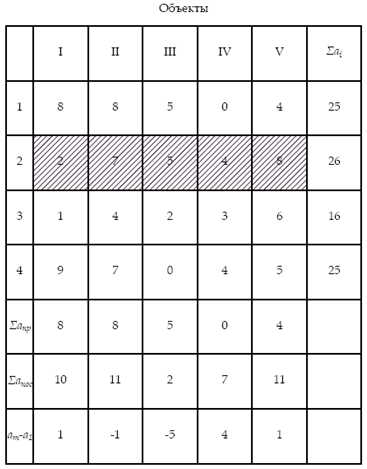
На основе данных дополнительных строк устанавливается рациональная очередность строительства объектов из следующих соображений:

а) на первом месте располагается объект с наибольшим значением Σа_пос . Остальные объекты располагаются так, чтобы Σа_пр постепенно возрастало, а Σа_пос снижалась к концу матрицы;

б) на первом месте располагается объект с наибольшим значением (а _m - а₁ ) , на последнем – с минимальным значением (а _m - а₁ ) ; остальные объекты располагаются так, чтобы (а _m - а₁ ) изменялось постепенно от максимального значения к минимальному.

Принятая очередность строительства объектов по п. а :

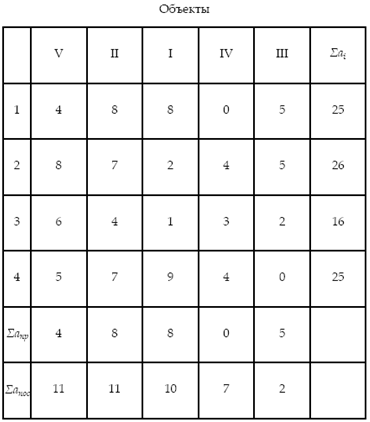
Принятая очередность строительства объектов по п. б :

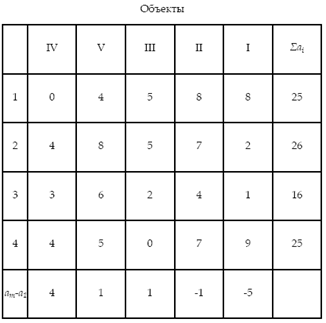
Найдем общую продолжительность строительства комплекса:

а) при исходной очередности объектов

Т₁ = (8 + 8 + 5 + 0 + 4) + (6 + 5 + 4) + (5 + 4) = 49;

б) при очередности объектов 5-2-1-4-3

Т₂ = (4 + 8 + 8 + 0 + 5) + (5 + 2 + 0) + (2 + 0) = 34;

в) при очередности объектов 4-5-3-2-1

Т₃ = (0 + 4 + 5 + 8 + 8) + (2 + 1 + 9) + (1 + 9) = 47.

Наименьшую продолжительность имеет очередность объектов 5-2-1-4-3.

Задание №5

Оптимизация сетевого графика по рабочим ресурсам

и по срокам строительства

Решить оптимизационные задачи управления строительством по сетевым моделям.

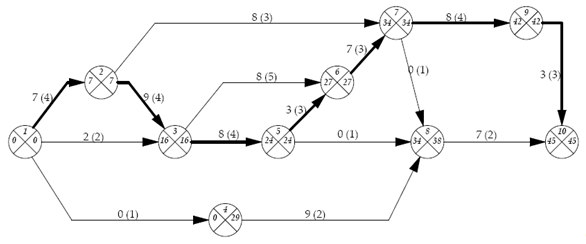
Т_общ = 45 дней

Данную сетевую модель можно оптимизировать. Для этого на критические пути увеличиваем количество рабочих, снимая их с менее загруженных участков. Таким образом, сокращаются сроки выполнения работ.

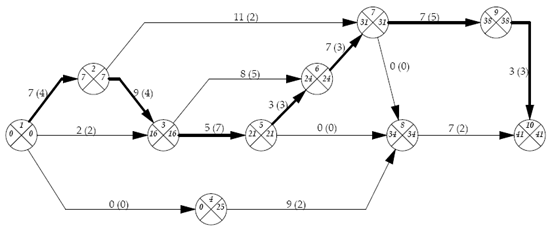
Т_общ. = 41 день