Название: СМО с отказами

Вид работы: реферат

Рубрика: Математика

Размер файла: 22.91 Kb

Скачать файл: referat.me-216320.docx

Краткое описание работы: СМО с отказами (задача Эрланга) Рассматривается N-канальная СМО с отказами: λпотерь λобслуживания υ υ υ λ Любая заявка может быть обслужена любым свободным каналом. Если все каналы заняты, заявка немедленно получает отказ в обслуживании и покидает систему (теряется).

СМО с отказами

СМО с отказами (задача Эрланга)

Рассматривается N-канальная СМО с отказами:

λпотерь

λобслуживания

υ

υ

υ

λ

ОА1

ОА2

ОАn

G

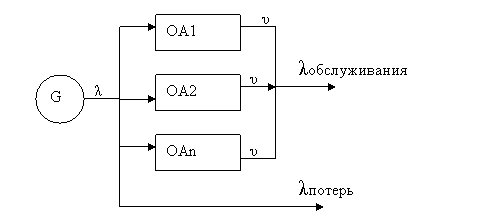
Любая заявка может быть обслужена любым свободным каналом. Если все каналы заняты, заявка немедленно получает отказ в обслуживании и покидает систему (теряется). Интенсивности входных и выходных потоков:

Считаем, что в этой системе имеются следующие потоки событий:

1) поступление заявок на вход СМО из источника заявок G;

2) обслуживание заявок в каналах.

Будем считать, что первый и второй потоки событий являются простейшими потоками с экспоненциальными законами распределения. Интервал поступления и обслуживания заявок соответственно имеют следующие характеристики:

1) интенсивность потока поступающих заявок характеризуется λ

2) интенсивность обслуживания одним каналом:

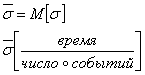
- мат.ожидание длительности обслуживания

Т.о. входной поток с интенсивностью λ и поток обслуживания с интенсивностью µ распределены по экспоненциальному закону и следовательно данные потоки являются простейшими, а сами процессы в системе Марковскими. Представим граф схему переходов для этого случая:

Состояния СМО в данном случае нумеруются по числу заявок, находящихся в СМО (в силу отсутствия очереди состояния, в котором находится система, совпадает с числом занятых каналов)

S0 - все каналы свободны, система свободна

S1 - занят один канал

Sk - заняты k каналов, остальные (n-k) свободны

Sn - заняты все n каналов

µ

2µ

(n-1)µ

nµ

λ

λ

λ

λ

λ

λ

S0

S1

S2

Sk

Sn-1

Sn

Из состояния Si-1 всегда с интенсивностью входного потока λ система переходит в следующее состояние Si, т.е. в данном случае будет заняе еще один канал и интенсивность перехода в следующее состояние равно интенсивности входного потока λ. Интенсивность обратного перехода возрастает с ростом числа параллельно работающих каналов. Чем больше их работает, тем интенсивнее процесс их освобождения. Для простейших потоков имеем:

Данная схема называется схемой гибели и размножения. Такое название происходит от того, что связаны соседние состояния. Математический аппарат - это Марковский процесс, с дискретными состояниями и непрерывным временем. Для заданной СМО матрица интенсивностей Λ имеет вид:

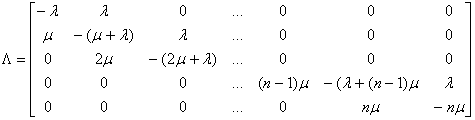
Пользуясь матрицей Λ запишем уравнения, которые позволяют рассчитать вероятности пребывания системы в каждом из указанных состояний. Распределение вероятностей P0,P1,…,Pn по состояниям S0,…,Sn определяется как решение системы дифференциальных уравнений.

P’(t)=P(t)Λ с начальными условиями:

P0(0)=1

Pi(0)=0, i=1,n;

Эти уравнения называются уравнениями Эрланга. Вероятности Рi характеризуют среднюю загрузку системы, в частности, Pn - это вероятность получения отказа в обслуживании, т.е. вероятность того, что все каналы заняты и все поступающие заявки будут потеряны. Тогда q=1-Pn - это вероятность обслуживания.

Зная эти вероятности, можно рассчитать различные характеристики эффективности системы.

А - среднее число заявок, обслуживаемых СМО в единицу времени или абсолютная пропускная способность СМО

Q - относительная пропускная способность СМО или вероятность обслуживания поступившей заявки