Название: Гетероскедастиканын салдары

Вид работы: реферат

Рубрика: Математика

Размер файла: 30.14 Kb

Скачать файл: referat.me-216328.docx

Краткое описание работы: 5.2. Гетероскедастиканың салдары Классикалық сызықтық регерссия моделін қарастыру барысында ЕКӘ ең жақсы сызықты ығыспаған бағаны береді, егер алғашқы шарттар орындалатын болғанда, солардың бірі ауытқу дисперсиясының тұрақтылығында (гомоскедастикалық):

Гетероскедастиканын салдары

5.2. Гетероскедастиканың салдары

Классикалық сызықтық регерссия моделін қарастыру барысында ЕКӘ ең жақсы сызықты ығыспаған бағаны береді, егер алғашқы шарттар орындалатын болғанда, солардың бірі ауытқу дисперсиясының тұрақтылығында (гомоскедастикалық):

Барлық бақылаулар і бойынша орындалады (і = 1,2,...,n ).

Егер бұл алғашқы шарт орындалмағада (гетероскедасткалық жағдайда), ЕКӘ қолдану төменгі жағдайларға келтіріледі. Коэффициенттер бағалар бұрынғыдай ығыспаған және сызықты.

1. Бағалаулар тиімді болмайды (яғни берілген параметрлер бағалауларына қарағанда олар ең кіші дисперсияға ие бола алмайды). Бағалау дисперсияның өсуі дәл бағалауды алу ықтималдығын кемітеді.

2. Бағалау дисперсиясы ығысу арқылы есептелінеді, регерессия теңдеуімен түсіндірілмеген дисперсия (m – түсіндірілетін айнымалылар саны) барлық коэффициенттердің дисперсиясының бағаларын есептеуде пайдалануда ол ығыспаған бағалау бола алмайды.

3. Жоғарыда айтылғандарға сәйкес, t және F статистикасы бойынша, ол сияқты аралықтар бағалаулар сенімді бола алмайды.

Олай болса, бағалау сапасының стандартын тексерудегі статистикалық көрсеткіштер қате болуы мүмкін, құрылған модельден басқа жағдайларда қате жағдайға келтіреді. Коэффициенттердің стандартты қателіктері төмен болады, олай болса t статистика мәні артуы мүмкін.

Гетероскедастикалық жағдайында ЕКӘ-нің тиімді болмау себебән төмендегі жұптық Ү белгілі бір у_і мәнін дисперсиясын тұрақты болмауына сәйкес бір мәні екіншісінен өзгеше болатын өз үлестірімі болатын жиыны жатады.

(у₁ және у_n мәндерінің үлестірімін салыстырыңдар).

ЕКӘ бойынша ауытқу квадраттарының қосындысы

минимумге зерттеледі.

Бұл жағдайда кіші дисперсия үлестірімі (мысалы, ) немесе үлкен дисперсия (мысалы, ) үлестіріміне сәйкес алынғанына қарамастан, берілген қосындыдағы әрбір нақты мәндері бірдей «салмаққа» ие болады. Бірақ бұл жағдай қайшылыққа келтіреді, себебі мейлінше аз дисперсия үлестірімімен алынған нүкте регрессия сызығы дәл анықтайды деген тұжырымға сәйкес келмейді.

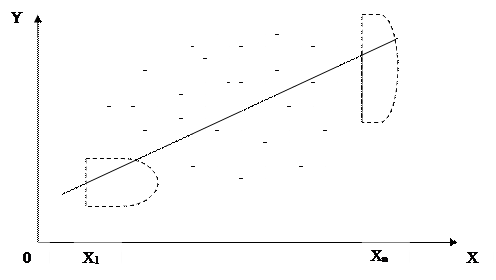5.3-сурет

Сонымен үлкен дисперсияға сәйкес келетін үлестіріммен алынған нүктеге қарағанда, ол үлкен «салмаққа ие» болады.

Сондықтан «салмақты» ескеретін бағалау әдісі дәл тиімді бағалауларды алуға мүмкіндік береді.

5.3. Гетероскедастикалық анықтау

Кейбір жағдайларда берілгендерін сипаттауды біле отырып гетероскедастикалық пайда болу проблемасын алдын ала білуге және ол қателікті болдырмау жолын ертерек анықтауға болады. Бірақ ол қателікті – проблеманы регрессия теңдеуінен құрғаннан кейін шешуге болады. Әрбір белгілі жағдайларда гетероскедастикалықты анықтау күрделі мәселе, себебі әрбір ауытқу дисперсиясы -ді анықтау үшін кездейсоқ Х шамасының мәніне Х_і -ге сәйкес келетін кездейсоқ Ү шамасының мәні Ү_і -ді білу қажет. Ал іс жүзінде әрбір Х_і -дің нақты мәндеріне Ү_і -дің тек қана бір мәні анықталады. Олай болу берілген Х_і үлкен кездейсоқ Ү шамасының дисперсиясын анықтауға мүмкін емес.

Х1

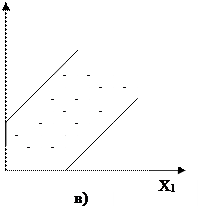
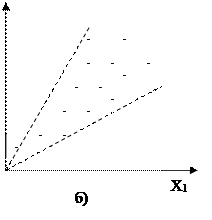
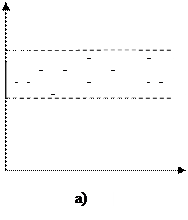
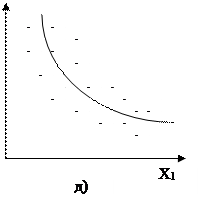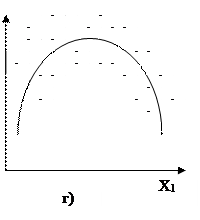
5.4 а суретте қателіктердің тұрақты екі бойынша орналасқан, ал 5.4 б квадраттық формаға сәйкес келеді, 5.4 д түсіндіруші айнымалылар мәні қисыққа жақын орналасқан, 5.4 г, д – статистикалық мәліметтердің көп бөлігін бейнелейді. Айта кету керек, жұптық регрессия жағдайында ауытқудың графиктік талдауы жеткілікті мөлшерде ыңғайлы және сенімді болады. Ал көптік регрессия жағдайында графиктік талдау әрбір түсіндіруші айнымалылар х_j үшін j=1,2,…,m тек қана жеке-дара қарастыру мүмкін болады.

Көптеген жадайда абцисса осіне Х -тің орнына регрессияның тәжірибелік теңдеуі бойынша алынған , (і =1,2,...,n ) мәндері құрылады. Себебі көптік регрессия теңдеуі түсіндіруші айнымалылар Х_і - лердің сызықты комбинациясы болады. Олай болса -дың -ге байланысын көрсететін график 5.4 б,в жағдайындағы гетероскедастикалықтың бар болуын көрсетеді. Мүмкін талдау көбінесе түсіндіруші айнымалылар үлкен болғанда маңызды.