Название: Центральная предельная теорема и ее доказательство через ряды Тейлора
Вид работы: реферат
Рубрика: Математика
Размер файла: 83.38 Kb
Скачать файл: referat.me-218014.docx
Краткое описание работы: Прежде чем приступить к рассмотрению центральной предельной теоремы, я считаю нужным сказать о слабой сходимости. Пусть задана последовательность случайных величин (далее с. в.)
Центральная предельная теорема и ее доказательство через ряды Тейлора
Прежде чем приступить к рассмотрению центральной предельной теоремы, я считаю нужным сказать о слабой сходимости.
Пусть задана последовательность случайных величин (далее с. в.) ![]() , задано некоторое распределение
, задано некоторое распределение ![]() с функцией распределения
с функцией распределения ![]() и
и ![]() — произвольная с. в., имеющая распределение
— произвольная с. в., имеющая распределение ![]() .
.
Определение.
Говорят, что последовательность с. в. ![]() при
при ![]() сходится слабо или по распределению к с. в.
сходится слабо или по распределению к с. в. ![]() и пишут:
и пишут: ![]() , или
, или ![]() , или
, или ![]() ,
,
если для любого ![]() такого, что функция распределения
такого, что функция распределения ![]() непрерывна в точке
непрерывна в точке ![]() , имеет место сходимость
, имеет место сходимость ![]() при
при ![]() .
.
Иначе говоря, слабая сходимость — это поточечная сходимость функций распределения во всех точках непрерывности предельной функции распределения.
Свойство 1.
Если ![]() , и функция распределения
, и функция распределения ![]() непрерывна в точках
непрерывна в точках ![]() и
и ![]() , то
, то
![]() и т.д. (продолжить ряд).
и т.д. (продолжить ряд).
Наоборот, если во всех точках ![]() и
и ![]() непрерывности функции распределения
непрерывности функции распределения ![]() имеет место, например, сходимость
имеет место, например, сходимость ![]() , то
, то ![]() .
.
Следующее важное свойство уточняет отношения между сходимостями.
Свойство 2.
1.
Если ![]() , то
, то ![]() .
.
2.
Если ![]() , то
, то ![]() .
.
Свойство 3.
1.
Если ![]() и
и ![]() , то
, то ![]() .
.
2.
Если ![]() и
и ![]() , то
, то ![]() .
.
Несколько содержательных примеров слабой сходимости я рассмотрю ниже. Но основной источник слабо сходящихся последовательностей и необычайно мощное и универсальное средство для асимптотического анализа распределений сумм независимых и одинаково распределенных случайных величин предоставляет нам центральная предельная теорема.
Я буду называть следующее утверждение «ЦПТ Ляпунова» (А. М. Ляпунов: 1901), но сформулирую и докажу теорему Ляпунова только в частном случае, т.е. для последовательности независимых и одинаково распределенных случайных величин.
Центральная предельная теорема.
Пусть ![]() — независимые и одинаково распределенные случайные величины с конечной и ненулевой дисперсией:
— независимые и одинаково распределенные случайные величины с конечной и ненулевой дисперсией: ![]() . Обозначим через
. Обозначим через ![]() сумму первых
сумму первых ![]() случайных величин:
случайных величин: ![]() .
.
Тогда последовательность случайных величин ![]() слабо сходится к стандартному нормальному распределению.
слабо сходится к стандартному нормальному распределению.
Доказательство.
Пусть ![]() — последовательность независимых и одинаково распределенных случайных величин с конечной и ненулевой дисперсией. Обозначим через
— последовательность независимых и одинаково распределенных случайных величин с конечной и ненулевой дисперсией. Обозначим через ![]() математическое ожидание
математическое ожидание ![]() и через
и через ![]() — дисперсию
— дисперсию ![]() . Требуется доказать, что
. Требуется доказать, что
![]()
Введем стандартизированные случайные величины ![]() — независимые с.в. с нулевыми математическими ожиданиями и единичными дисперсиями. Пусть
— независимые с.в. с нулевыми математическими ожиданиями и единичными дисперсиями. Пусть ![]() есть их сумма
есть их сумма ![]() . Требуется доказать, что
. Требуется доказать, что
![]()
Характеристическая функция величины ![]() равна
равна
![]()
Характеристическую функцию с.в. ![]() можно разложить в ряд Тейлора, в коэффициентах которого использовать известные моменты
можно разложить в ряд Тейлора, в коэффициентах которого использовать известные моменты ![]() ,
, ![]() . Получим
. Получим
![]()
Подставим это разложение, взятое в точке ![]() , в равенство и устремим
, в равенство и устремим ![]() к бесконечности. Еще раз воспользуемся замечательным пределом:
к бесконечности. Еще раз воспользуемся замечательным пределом:
![]()
В пределе получили характеристическую функцию стандартного нормального закона. По теореме о непрерывном соответствии можно сделать вывод о слабой сходимости :
![]()
распределений стандартизованных сумм к стандартному нормальному распределению, что и утверждается в ЦПТ.
Пользуясь определением и свойствами слабой сходимости, и заметив, что функция распределения ![]() любого нормального закона непрерывна всюду на
любого нормального закона непрерывна всюду на ![]() , утверждение ЦПТ можно сформулировать любым из следующих способов:
, утверждение ЦПТ можно сформулировать любым из следующих способов:
Следствие.
Пусть ![]() — независимые и одинаково распределенные случайные величины с конечной и ненулевой дисперсией. Следующие утверждения эквивалентны друг другу и равносильны утверждению ЦПТ.
— независимые и одинаково распределенные случайные величины с конечной и ненулевой дисперсией. Следующие утверждения эквивалентны друг другу и равносильны утверждению ЦПТ.
· Для любых вещественных ![]() при
при ![]() имеет место сходимость
имеет место сходимость
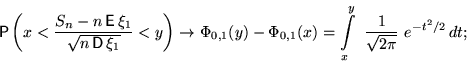
· Для любых вещественных ![]() при
при ![]() имеет место сходимость
имеет место сходимость
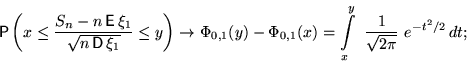
· Для любых вещественных ![]() при
при ![]() имеет место сходимость
имеет место сходимость
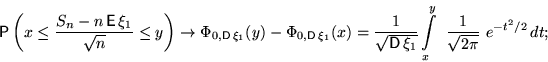
· Если ![]() — произвольная с. в. со стандартным нормальным распределением, то
— произвольная с. в. со стандартным нормальным распределением, то
![]()
Следствием из ЦПТ является предельная теорема Муавра-Лапласа.
Предельная теорема Муавра — Лапласа.
Пусть ![]() — событие, которое может произойти в любом из
— событие, которое может произойти в любом из ![]() независимых испытаний с одной и той же вероятностью
независимых испытаний с одной и той же вероятностью ![]() . Пусть
. Пусть ![]() — число осуществлений события
— число осуществлений события ![]() в
в ![]() испытаниях. Тогда
испытаниях. Тогда ![]() .
.
Иначе говоря, для любых вещественных ![]() при
при ![]() имеет место сходимость
имеет место сходимость
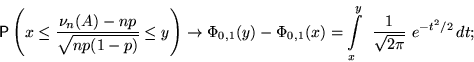
Доказательство.
По-прежнему ![]() есть сумма независимых, одинаково распределенных с. в., имеющих распределение Бернулли с параметром, равным вероятности успеха
есть сумма независимых, одинаково распределенных с. в., имеющих распределение Бернулли с параметром, равным вероятности успеха ![]() :
:

![]()
Осталось воспользоваться ЦПТ.
Ниже я рассмотрю примеры использования ЦПТ.
Пример 1 .
З а д а ч а. Монета подбрасывается 10000 раз. Оценить вероятность того, что частота выпадения герба отличается от вероятности более чем на одну сотую.
Р е ш е н и е. Требуется найти ![]() , где
, где ![]() ,
, ![]() — число выпадений герба, а
— число выпадений герба, а ![]() — независимые с. в., имеющие одно и то же распределение Бернулли с параметром 1/2. Домножим обе части неравенства под знаком вероятности на
— независимые с. в., имеющие одно и то же распределение Бернулли с параметром 1/2. Домножим обе части неравенства под знаком вероятности на ![]() и поделим на корень из дисперсии
и поделим на корень из дисперсии ![]() одного слагаемого.
одного слагаемого.
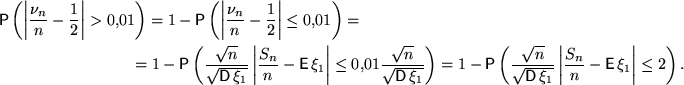
Согласно ЦПТ или предельной теореме Муавра — Лапласа, последовательность
![]()
слабо сходится к стандартному нормальному распределению. Рассмотрим произвольную с. в. ![]() , имеющую распределение
, имеющую распределение ![]() .
.
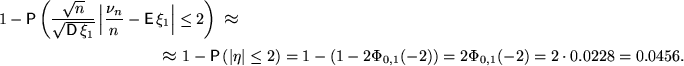
Пример 2.
Прекрасным примером ЦПТ в экономике может служить ее использование в страховом деле. В большинстве случаев конкретный вид распределения потерь (размеров отдельных требований о выплате страховых сумм) не играет существенной роли, поскольку сумма исков, предъявляемых страховщику (величина суммарного иска), обычно зависит только от средней величины и дисперсии убытка. Дело в том, что если количество страховых случаев значительно превышает единицу, то в силу центральной предельной теоремы распределение суммарного иска является нормальным распределением. Обозначив его дисперсию как DZ , а математическое ожидание (среднее значение суммарного иска) как < Z> = < N>< Q>
- где <N>, <Q> - среднее значение числа страховых случаев и величины страховой выплаты, получаем следующее выражение для рисковой надбавки Тr :
Т r = [( Т 0 * a )/(< N > * < Q >)] * (< N > * D Q + < Q >2 * D N ) 0.5
- где DQ и DN -дисперсии величины страховой выплаты и количества страховых случаев.
В простейшем случае, когда все выплаты одинаковы (а, следовательно, их дисперсия равна нулю), имеем:
Т r = ( Т 0 * a )/ N 0.5
Эта формула также дает неплохое приближение, если коэффициент вариации уровня страховых выплат значительно меньше единицы.
При включении в страховой полис нескольких независимых рисков ожидаемая величина страховых выплат в соответствии с теоремой о сложении вероятностей представляет собой сумму ожидаемых страховых выплат по каждому риску в отдельности, а рисковая надбавка вычисляется как среднеквадратичная величина всех рисковых надбавок.
Похожие работы
-
Строгое притяжение к нормальному закону для стационарных последовательностей с равномерно сильным перемешиванием
Гипотеза (Ибрагимов-Иосифеску).
-
Предельные теоремы. Характеристические функции
Теория вероятностей и закономерности массовых случайных явлений. Неравенство и теорема Чебышева. Числовые характеристики случайной величины. Плотность распределения и преобразование Фурье. Характеристическая функция гауссовской случайной величины.
-
Распределение Гаусса. Центральная предельная теорема теории вероятностей. Распределения Пирсона и Стьюдента
Впервые нормальный закон был обнаружен в 19 веке в применении к теории ошибок измерения Лапласом и Гаусcом.
-
Высшая математика
Основные теоремы и определения.
-
Повторные ряды
План работы Введение……………………………...………………….…… 5 §1 Повторные ряды ……………….......................................... 6 §2. Сходимость повторных рядов …………………………... 7
-
Теория вероятности 3
Вероятность (вероятностная мера) — мера достоверности случайного события. Оценкой вероятности события может служить частота его наступления в длительной серии независимых повторений случайного эксперимента. Согласно определению П. Лапласа мерой вероятности называется дробь, числитель которой есть число всех благоприятных случаев, а знаменатель - число всех возможных случаев.
-
Числовые ряды
ВЫСШАЯ МАТЕМАТИКА Числовые ряды Содержание Лекция. Числовые ряды 1. Определение числового ряда. Сходимость 2. Основные свойства числовых рядов 3. Ряды с положительными членами. Признаки сходимости
-
Степенные ряды
Определение степенного ряда. Теорема Абеля как определение структуры области сходимости степенного ряда. Свойства степенных рядов. Ряды Тейлора, Маклорена для функций. Разложение некоторых элементарных функций в ряд Маклорена. Приложения степенных рядов.
-
Измеримые функции
Определение и простейшие свойства измеримой функции. Дальнейшие свойства измеримых функций. Последовательности измеримых функций. Сходимость по мере. Структура измеримых функций. теоремы о приближении измеримых функций.
-
Законы больших чисел
Теорема Бернулли как простейшая форма закона больших чисел. Предельные теоремы теории вероятностей и объяснение природы устойчивости частоты появлений события. Качественные и количественные утверждения закона больших чисел, его практическое применение.