Название: Методы решения текстовых задач
Вид работы: реферат
Рубрика: Математика
Размер файла: 60.77 Kb
Скачать файл: referat.me-218373.pptx
Краткое описание работы: Слушатель ОП «Математическое образование в основной и средней школе» Шаронова Мария Викторовна Содержание: - Введение 3 - 1. Составные части задачи и требования по ее решению в школьном
Методы решения текстовых задач
Слушатель ОП «Математическое образование в основной и средней школе»
Шаронова Мария Викторовна
Содержание:
- Введение 3
- 1. Составные части задачи и требования по ее решению в школьном
- курсе математики 4
- 2.Метод математического моделирования при решении текстовых задач. 6
- 2.1. Понятие модели и моделирования. 6
- 2.2. Моделирование при решении задач. 10
- 2.2.1.Задачи на встречное движение двух тел. 13
- 2.2.2.Задачи на движение двух тел в одном направлении. 14
- 2.2.3.Задачи на движение двух тел в противоположных направлениях. 15
- 2.3.Опытно-практическая работа по сопоставлению применяемых
- способов решения задач в 5 и 9 классов. 17
- Заключение 18
- Приложение.
- Список литературы.
Методы решения задач
- - анализ и синтез
- - метод сведения к ранее решённым
- - метод математического
моделировавния
- - метод математической индукции
- - метод исчерпывающих проб
Метод математического моделирования
«В процессе математического моделирования выделяют три этапа:
1. Формализация – перевод предложенной задачи (ситуации) на язык
математической теории (построение математической модели задачи).
2. Решение задачи в рамках математической теории (говорят: решение внутри модели).
3.Перевод результата математического решения задачи на тот язык, на котором была сформулирована исходная задача (интерпретация решения).»
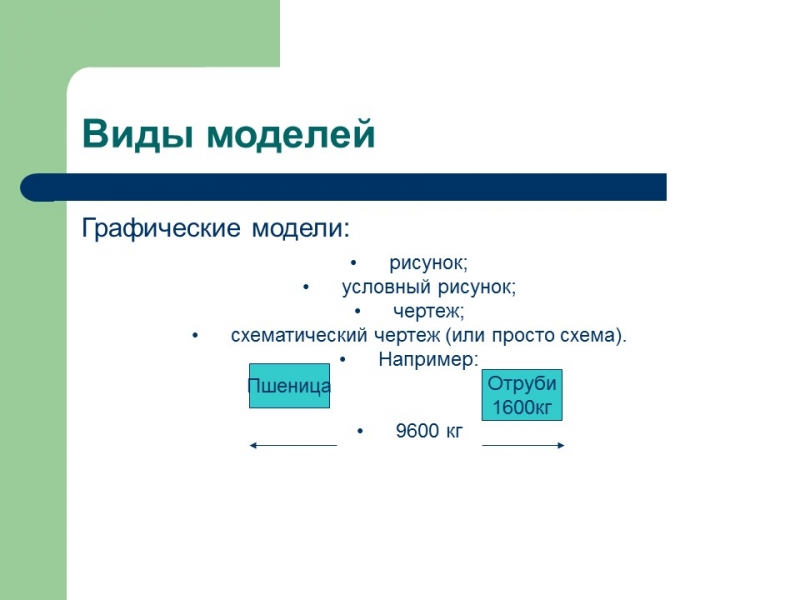
Виды моделей
Графические модели:
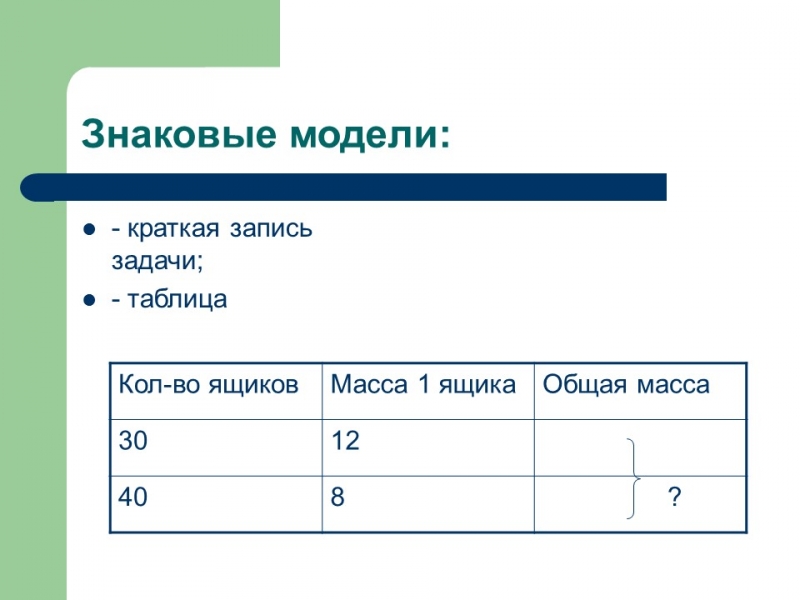
Знаковые модели:
- - краткая запись задачи;
- - таблица
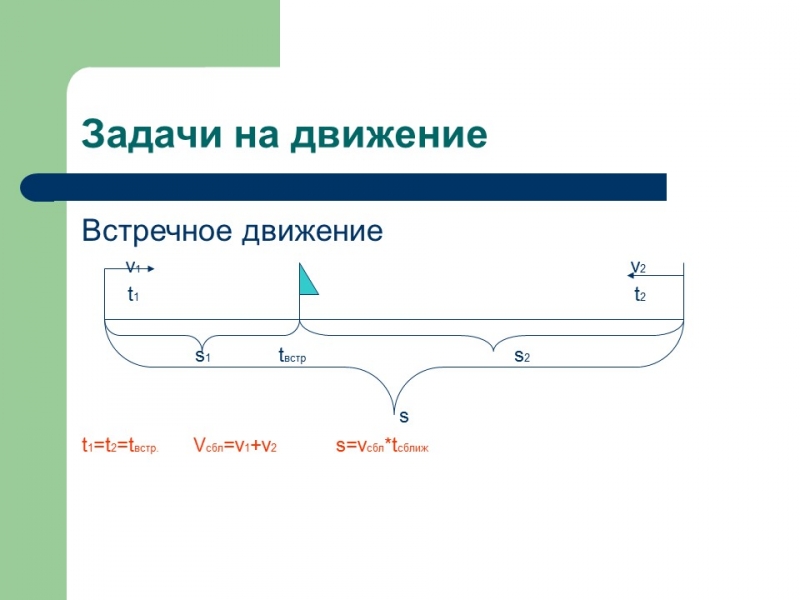
Задачи на движение
Встречное движение
v1 v2
t1 t2
s1 tвстр s2
s
t1=t2=tвстр. Vсбл=v1+v2 s=vсбл*tсближ
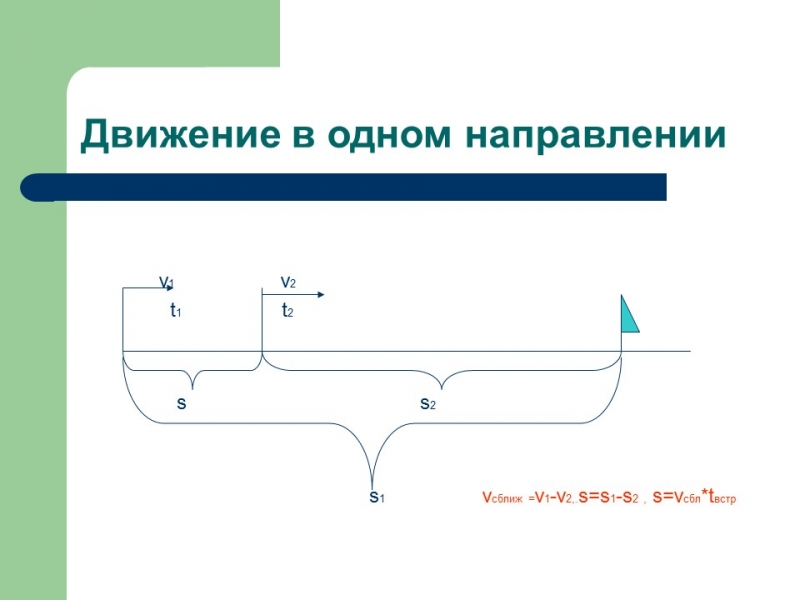
Движение в одном направлении
v1 v2
t1 t2
s s2
s1 vсближ =v1-v2,.s=s1-s2 , s=vсбл*tвстр
Движение в противоположных направлениях
В таких задачах два тела могут начинать движение в противоположных направлениях из одной точки:
а) одновременно;
б) в разное время.
А могут начинать свое движение из двух разных точек, находящихся на заданном расстоянии, и в разное время.
Общим теоретическим положением для них будет следующее:
v удал. = v1+ v2, где v1 и v2 соответственно скорости первого и второго тел.
(Схематический чертеж строится аналогично предыдущим).
Заключение
В школьном курсе нет четкого разделения методов, в том смысле, что авторы школьных учебников не дают напрямую схему какого либо метода. Поэтому, решая задачи любого типа, пусть даже наиболее удобным методом не стоит забывать о других способах её решения.






Похожие работы
-
Роль прикладной математики в подготовке учителей математики и информатики
В статье обсуждаются вопросы вузовской подготовки учителей математики и информатики по дисциплинам прикладной математики. Приводятся примеры изучения дисциплин прикладной математики с точки зрения особенностей конкретного профиля подготовки студентов.
-
Системы (комплексы) общетехнических и организационно-методических национальных стандартов
Национальные и межгосударственные стандарты устанавливают общие организационно-методические и организационно-нормативные положения для определенной области деятельности, а также общетехнические требования, нормы и правила.
-
Соотношение между сторонами и углами прямоугольного треугольника
Конспект урока по геометрии для 8 класса средней общеобразовательной школы Тема урока: Соотношение между сторонами и углами прямоугольного треугольника
-
О курсе “Элементы теории Галуа”
Возникнув сначала внутри математики, навыки исследовательской деятельности будут перенесены в профессиональную сферу. В силу этого важно пробудить у будущего учителя математики интерес к предмету, привить ему навыки самостоятельной творческой работы.
-
Атом
За триста с лишним лет до нашей эры в Древней Греции ученые-философы рассуждали так: любое вещество, любой предмет можно разделить на части. Камень можно раздробить в мелкий порошок. Воду — расплескать, а потом она испарится, превратится в пар.
-
Исследование метода продолжения решения по параметру для нелинейных САУ
Поиск корней нелинейных САУ с помощью метода продолжения решения по параметру. Математическое описание метода. Программное обеспечение для построения графиков сходимости метода. Требования к программному обеспечению и описание логической структуры.
-
Функционально-графический подход к решению задач с параметрами
Выполнение алгебраических преобразований, логическая культура и техника исследования. Основные типы задач с параметрами, нахождение количества решений в зависимости от значения параметра. Основные методы решения задач, методы построения графиков функций.
-
Использование информационно-коммуникативных технологий при изучении темы "Показательной функции" в средней школе
Новые информационно-коммуникационные технологии в современном школьном образовании. Применение программных обеспечений при срезе и контроля знаний по теме "Показательная функция". Роль использования компьютерных технологий в преподавании математики.
-
Методика обучения по курсу математики за 3 года
Работая над методической темой школы в течение трёх лет, МО учителей математики ставило перед собой следующие цели: Строить учебный процесс с учетом индивидуальности каждого ребёнка: его потребностей, мотивов, активности, интеллекта.
-
Электронные учебники
Развитие информационных и телекоммуникационных технологий и электронного оборудования открывает новые возможности дистанционного образования при относительно низкой себестоимости.