Название: Оценка прочности бруса в условиях сильной нагрузки

Вид работы: контрольная работа

Рубрика: Физика

Размер файла: 798.58 Kb

Скачать файл: referat.me-340465.docx

Краткое описание работы: СОДЕРЖАНИЕ 1. Оценка статической нагрузки на брус Определение диаметра вала из условия прочности Уточнение диаметра из условия жёсткости Конструирование вала

Оценка прочности бруса в условиях сильной нагрузки

СОДЕРЖАНИЕ

1. Оценка статической нагрузки на брус

1.1 Определение диаметра вала из условия прочности

1.2 Уточнение диаметра из условия жёсткости

1.3 Конструирование вала

2. Оценка динамической нагрузки на брус

2.1 Расчёт вала на прочность и жёсткость при крутящем ударе

2.2 Расчёт вала на прочность при вынужденных колебаниях

2.3 Определение критических оборотов вала

3. Проектирование бруса в условиях переменной нагрузки

3.1 Определение параметров цикла нормальных напряжений

3.2 Определение параметров цикла касательных напряжений

3.3 Определение эффективных коэффициентов концентрации напряжений

3.4 Определение коэффициента запаса прочности по 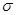и

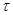
3.5 Определение общего коэффициента запаса прочности

3.6 Проверка прочности вала с учётом колебаний

СПИСОК ЛИТЕРАТУРЫ

1. Оценка статической нагрузки на брус

1.1 Определение диаметра вала из условия прочности

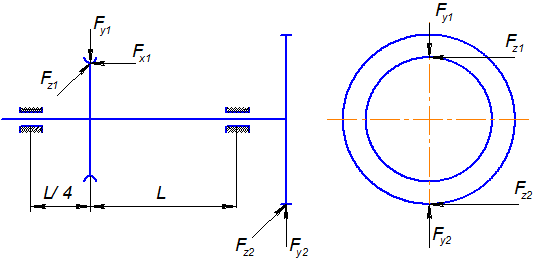
Материал: 12ХНВА

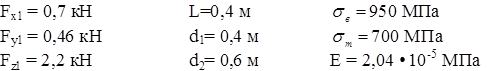
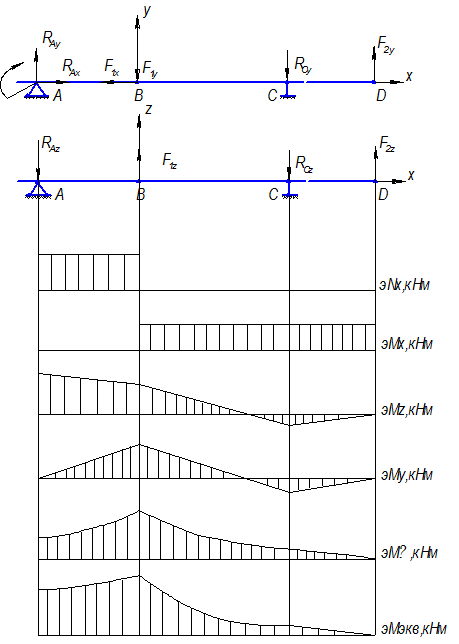
Для заданной схемы вала определяем из условия равновесия недостающие внешние факторы и приводим их к оси вала, разложив на составляющие в плоскостях XY и XZ

;

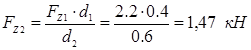
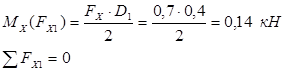
Выбираем расчётную схему вала:

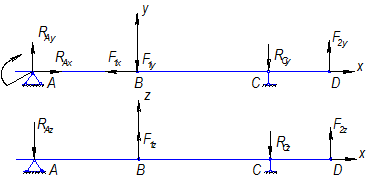
Определение реакций в плоскостиХУ :

;

;

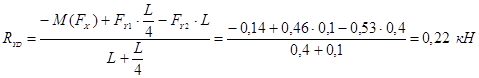
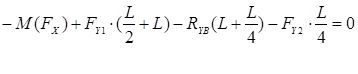
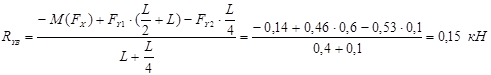
Проверка:

;

;

Определение реакции в плоскости ХУ:

;

;

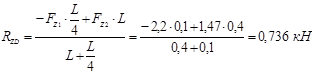
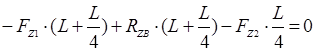
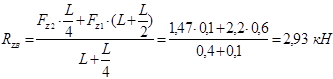
Проверка:

;

Построим эпюры ,,,:

:

;

;

;

:

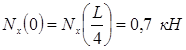
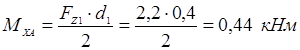
а);

б);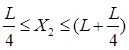

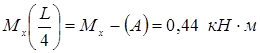
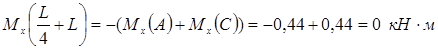
в);

:

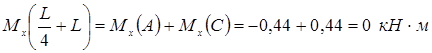
а);

б) ;

в);

:

а) ;

б);

в);

Построим эпюры и :

:

а);

б);

в);

:

а);

б);

в);

Построим алгоритм для определения диаметра вала из условия прочности в опасном сечении:

;

;

;

;

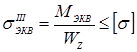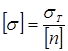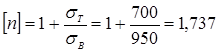
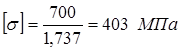
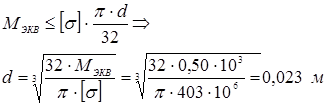
Примем d = 25 мм.

Проверка прочности

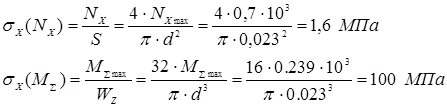
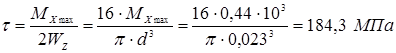
По третьей теории прочности:

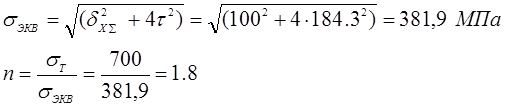
условие прочности не выполняется для вала d = 25мм

Подбор подшипников качения для вала

На опоре С устанавливаем радиальный шариковый подшипник с допускаемым углом поворота

На опоре А устанавливаем радиально-упорный шариковый подшипник с допускаемым углом поворота

1.2 Уточнение диаметра вала из условия жесткости

Определим прогиб вала

Поскольку присутствует линейная эпюра, используем правило Верещагина:

;

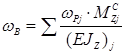Чтобы определить прогиб, строим единичную систему и эпюры моментов от единичной силы, для этого приложим в точке С силу F=1H.

Определение реакций:

;

;

;

;

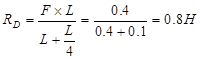
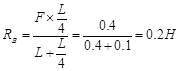
Проверка:

;

Построение эпюруот единичной силы:

а);

б);

в);

Определение прогибов:

Плоскость	J	ωPj,кН·м²	MjB,м	MjB·ωPj,кН·м³
XAY(ЭMz)	1	0.0023	0	0
	2	0.0047	0	0
	3	0.0141	0.02	0.000282
	4	-0,0012	-0.073	0.0000876
	5	-0,0012	-0,053	0.0000636
	Σ	0.0004332
XAZ(ЭMy)	1	0,011	0	0
	2	0,033	0,02	0.00066
	3	-0,0036	-0,074	0,002442
	4	-0,0036	-0,053	0,00019
	Σ	0.0032928

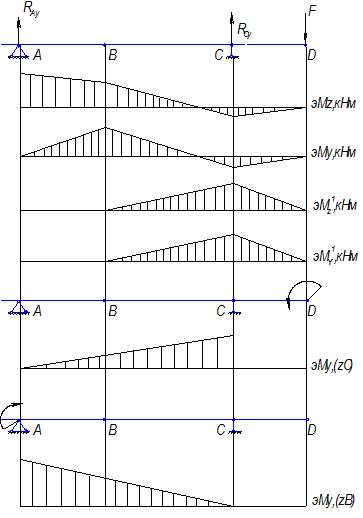
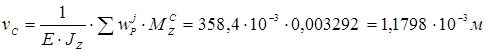
Определим углы поворота в местах расположения опор:

Определение угла поворота в вертикальной() и горизонтальной () плоскостях, полный угол поворота () сечений вала в месте расположения опор, считая диаметр вала постоянным:

;

;

Прикладываем в точках А и С единичные моменты 1Нм;

Плоскость	J	ωPj, кН·м²	MjB, м	MjD, м	MjB·ωPj, кН·м³	MjD·ωPj, кН·м³
XAY(ЭMz)	1	0.0023	0	0	0	0
	2	0.0047	0	0	0	0
	3	0.0141	0.2	0.8	0.00282	0.0113
	4	-0,0012	0.74	0.25	-0,00089	-0.0003
	5	-0.0012	0.867	0.133	-0,00104	-0.00016
	Σ	0.00089	0,010
XAZ(ЭMy)	1	0,011	0	0	0	0
	2	0,033	0.18	0.789	0,0059	0.026
	3	-0,0036	0.73	0.267	-0,0026	-0.00096
	4	-0.0036	0.845	0.133	-0,00304	-0.00047
	Σ	0.00026	0.0245

Проверка жесткости вала:

;

Условие жесткости:

<условие жесткости не выполняется

>условие жесткости выполняется

<условие жесткости не выполняется

Пересчёт диаметра вала из условия жесткости:

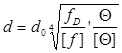
По :

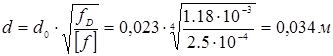
По :

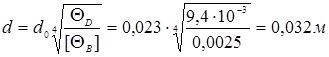
По :

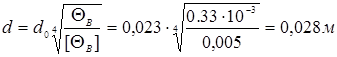
Из условия жесткости принимаем

1.3 Конструирование вала

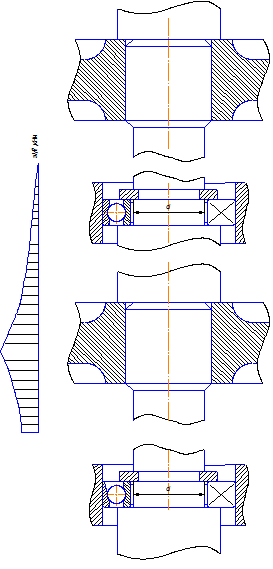
2. Оценка динамической нагрузки на брус

2.1 Расчёт вала на прочность и жёсткость при крутящем ударе

Определим динамический крутящий момент:

;

;

;

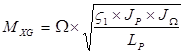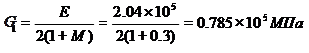
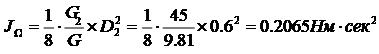
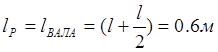
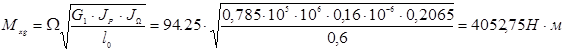
Построение эпюры :

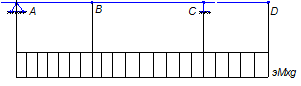
Проверим прочность:

<

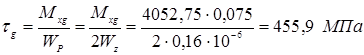
>условие прочности не выполняется

Проверим жёсткость:

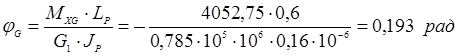
условие жесткости не выполняется.

2.2 Расчёт вала на прочность при вынужденных колебаниях

Определим собственную круговую частоту вала:

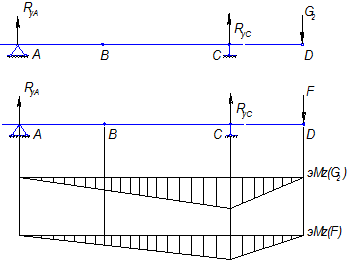
Определим реакции от силыв точках расположения опор

:

:

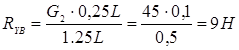
Проверка:

:

:

Определим реакции от единичной силыв точках расположения опор:

;

;

;

;

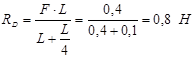
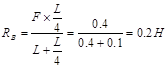
Проверка:

;

:

Определение прогиба:

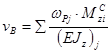
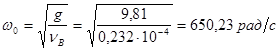
Определим силу инерции, действующую на вал :

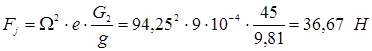
Построим эпюру изгибающих моментов от и :

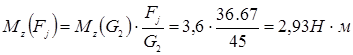
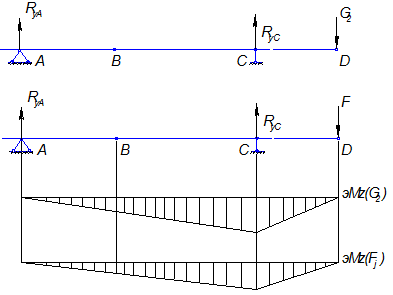
Определим коэффициент увеличения амплитуды колебаний, считая вынуждающей силой, а вынужденной круговой частотой:

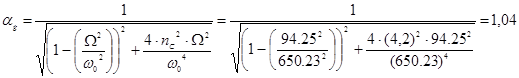
Определим коэффициент динамичности:

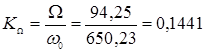
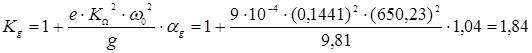
Проверим прочность по :

<условие прочности выполняется

Определим прогиб в месте расположения D2:

< условие жёсткости выполняется

2.3 Определение критических оборотов вала

Построим график зависимости от без учёта и с учётом сил сопротивления

При :

При :

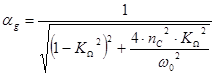
	0	0,2	0,4	0,6	0,8	1	1,2	1,4	1,6	1,8	2
	1	1,04	1,19	1,56	2,77	171,4	2,27	1,04	0,64	0,44	0,33
	1	1,04	1,19	1,56	2,77	171,4	2,27	1,04	0,64	0,44	0,33

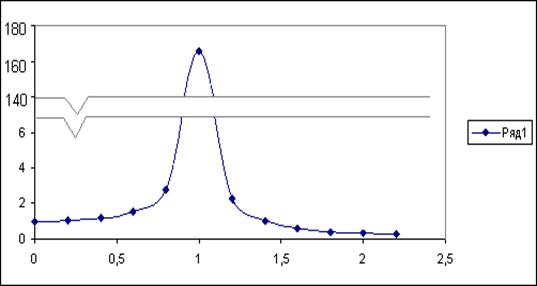
Вывод об отношении вала к "гибким" или "жёстким" системам:

<вал относится к "жёстким" системам

Определим критические обороты:

условие прочности выполняется

Запас прочности по :

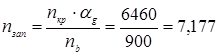
3. Проектирование бруса в условиях переменной нагрузки

Состояние поверхности в зоне концентратора: полировка

3.1 Определение параметров цикла нормальных напряжений

3.2 Определение параметров цикла касательных напряжений

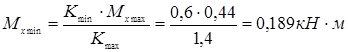
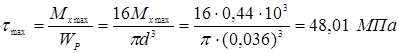
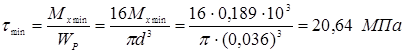
3.3 Определение эффективных коэффициентов концентрации напряжений

Определим эффективные коэффициенты концентрации напряжений в сечении , где находится зубчатое колесо.

Суммарный момент достигает максимума в месте крепления радиального роликового подшипника, поэтому расчет на прочность проводим для точки :

Для ступенчатого перехода с галтелью:

Для отверстия в валу:

Масштабные коэффициенты при :

Учитывая состояние обработки поверхности, определим коэффициент качества поверхности:

Определение эффективных коэффициентов концентрации детали:

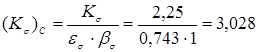
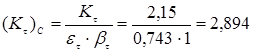
Находим коэффициенты чувствительности материала к асимметрии цикла:

3.4 Определение коэффициента запаса прочности по и

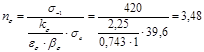
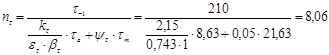
3.5 Нахождение общего коэффициента запаса прочности

> -

видно, что прочность вала обеспечивается

3.6 Проверка прочности вала с учётом колебаний

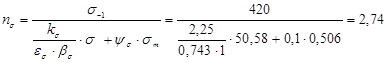
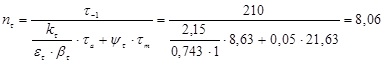
видно, что прочность вала обеспечивается даже с учётом колебаний

СПИСОК ЛИТЕРАТУРЫ

1. Феодосьев В. И. "Сопротивление материалов" : Учеб. для вузов. - М.: Изд-во МГТУ им Н. Э. Баумана, 2000

2. Писаренко Г. С., Яковлев А. П., Матвеев В. В. "Справочник по сопротивлению материалов". - Киев: Наук. думка, 1988

3. Дунаев П. Ф., Леликов О. П. "Конструирование узлов и деталей машин": Учеб. Пособие для машиностроит. спец. вузов - М.: Высш. шк., 1985

4. Гафаров Р. Х., Жернаков В. С. "Что нужно знать о сопротивлении материалов" - М.: Машиностроение, 2001