Название: Спиновый дихроизм нейтронов и ядерный псевдомагнетизм
Вид работы: курсовая работа
Рубрика: Физика
Размер файла: 73.66 Kb
Скачать файл: referat.me-341121.docx
Краткое описание работы: Амплитуда рассеяния нейтрона в ядерной среде, показатели ее преломления. Зависимость поляризации и угла поворота от пройденного нейтронным пучком расстояния. Энергия нейтрона в ядерной среде. Получение выражения для ядерного псевдомагнитного поля.
Спиновый дихроизм нейтронов и ядерный псевдомагнетизм
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ
УЧРЕЖДЕНИЕ ОБРАЗОВАНИЯ
«БРЕСТСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ имени А.С. Пушкина»
КУРСОВАЯ РАБОТА
по теоретической физике
Спиновый дихроизм нейтронов и ядерный псевдомагнетизм
Брест, 2010
Оглавление
Введение
1.1 Спиновый дихроизм нейтронов
1.2. Ядерный псевдомагнетизм
2.1 Получение выражения для амплитуды рассеяния нейтрона в ядерной среде
2.2 Существование 2 показателей преломления ядерной среды
2.3 Расчет зависимости поляризации от пройденного нейтронным пучком расстояния и зависимости угла поворота от расстояния
2.4 Энергия нейтрона в ядерной среде. Зависимость от направления спина нейтрона по отношению к вектору поляризации ядер
2.5 Получение выражения для ядерного псевдомагнитного поля
Заключение
Список использованной литературы
Введение
Спиновый дихроизм проявляется в асимметрии пропускания через образец поляризованных нейтронов с разным спином, а также в появлении продольной поляризации при прохождении через вещество первоначально неполяризованных нейтронов. По-иному, дихроизм – это существование 2 показателей преломления для частиц с различным знаком проекции спина (спиральности).
Это явление возникает в обычной оптике из-за разницы в полных сечениях рассеяния для состояний фотона с различной спиральностью «+» и «–», а в нейтронной оптике из-за разницы в полных сечениях рассеяния для состояний нейтрона с различной проекцией спина «+» и «–». С другой стороны, мнимая часть амплитуды или коэффициента преломления связана с полным сечением по оптической теореме, следовательно, нейтроны, имеющие разную спиральность, будут по-разному поглощаться в веществе, в результате либо появляется поляризация первоначально неполяризованного пучка, либо разный коэффициент пропускания для нейтронов, поляризованных вдоль и против импульса.
1.1 Спиновый дихроизм нейтронов
Дихроизм (от греч. díchroos - двухцветный) - один из видов проявления плеохроизма, различная окраска одноосных кристаллов (обладающих двойным лучепреломлением) в проходящем свете при взаимно перпендикулярных направлениях наблюдения - вдоль оптической оси и перпендикулярно к ней. Например, кристалл апатита, освещаемый белым светом, кажется на просвет светло-жёлтым, если смотреть по направлению оптической оси, и зелёным - в перпендикулярном направлении. Окраску кристалла в указанных условиях наблюдения называют, соответственно, "осевой" и "базисной". При прочих направлениях наблюдения кристалл также виден окрашенным (в какой-либо из промежуточных цветов), т. е. дихроизм представляет собой частный случай плеохроизма как многоцветности кристаллических фаз. Дихроизм обусловлен различием спектров поглощения кристалла для световых лучей, имеющих разное направление и поляризацию. Для одноосных кристаллов различают две "главные" (основные) окраски - при наблюдении вдоль оптической оси и перпендикулярно к ней [6].
А теперь с помощью таблицы рассмотрим, в чем сходство спинового дихроизма нейтронов с эффектом Фарадея
Таблица 1.1 – Сравнительная характеристика спинового дихроизма нейтронов с эффектом Фарадея
| эффект Фарадея | ядерная прецессия спина нейтрона | |
| частица | фотон | Медленные нейтроны |
| среди каких частиц движется | Поляризованные по спину электроны | Поляризованные по спину ядра |
| наличие спиновой поляризации | Да (электроны) | Да (ядра) |
| в чем проявляется дихроизм | Различные показатели преломления и коэффициенты поглощения для фотона | Различные показатели преломления и коэффициенты поглощения для нейтрона |
| сущность эффекта | Плоскость поляризации поворачивается на угол |
По мере прохождения в глубь мишени с поляриз. ядрами вектор поляризации нейтрона поворачивается на
|
| кто открыл | Фарадей, 1845г. | Группы Абрагама и Форте, 1970-е г. (предсказана в 1964 г. В. Г. Барышевским и М. И. Подгорецким) |
1.2 Ядерный псевдомагнетизм
Нейтрон, как известно, обладает спином и собственный магнитный момент. Известно ,что любая частица обладающая собственным магнитным моментом при попадании в обычное магнитное поле испытывает прецессию собственного магнитного момента (ларморовская прецессия). Следовательно, должен испытывать ее и нейтрон. Но когда нейтрон оказывается среди поляризованных ядер, то прецессию испытывает не собственный магнитный момент, а спин. Но поскольку спин неразрывно связан с магнитным моментом, то это все равно что если бы воздействие поляризованных ядер на нейтрон можно было бы представить в виде поля, чем то похожее на магнитное, действующее на собственный магнитный момент нейтрона (как при ларморовской прецессии), но имеющего совсем иную природу (ядерную).
Данный обзац можно отобразить в виде сравнительной характеристики обычного магнитного поля и ядерного псевдомагнитного поля
Таблица 1.2 - Сравнительная характеристика обычного магнитного поля и ядерного псевдомагнитного поля
| Характеристики | Магнитное поле | Ядерное псевдомагнитное поле |
| 1.Каким фундаментальным взаимодействием обусловлено? | Электромагнитным | ядерным |
| 2. Может ли его воздействию подвергаться электрон, протон, нейтрон? | Да; да; да | Нет; да; да |
| 3. Может ли создаваться движущими заряженными частицами? | Да | Нет |
| 4. Возможно ли квантование энергии по Ландау для частицы в таком поле? | Да | Нет |
| 5. Какой тип прецессии спина (или магн. момента) нейтрона наблюдаться в таком поле? | ларморовская | ядерная |
| 6. Опыт по разделению пучков поляризованных частиц в соответствующем поле? | Штерна - Герлаха | Работы групп Абрагама и Форте |
| 7. Может ли существовать в вакууме? | Да | Нет |
Волновая функция
Волновая функция (функция состояния, пси-функция, амплитуда вероятности) — комплексная функция, используемая в квантовой механике для вероятностного описания состояния квантовомеханической системы. В широком смысле — то же самое, что и вектор состояния.
Вариант названия «амплитуда вероятности» связан со статистической интерпретацией волновой функции: вероятность нахождения частицы (или физической системы) в данном состоянии равна квадрату абсолютного значения амплитуды вероятности этого состояния.
Волновая функция зависит от координат (или обобщённых координат) системы и формируется таким образом, чтобы квадрат её модуля представлял собой плотность вероятности (для дискретных спектров — просто вероятность) обнаружить систему в положении, описываемом координатами.
Набор координат, которые выступают в роли аргументов функции, представляет собой полный набор физических величин, которые можно измерить в системе. В квантовой механике возможно выбрать несколько полных наборов величин, поэтому волновая функция одного и того же состояния может быть записана от разных аргументов. Выбранный для записи волновой функции полный набор определяет представление волновой функции. Так, возможны координатное представление, импульсное представление, в квантовой теории поля используется вторичное квантование и представление чисел заполнения или представление Фока и др.
Если волновая функция, например, электрона в атоме, задана в координатном представлении, то квадрат модуля волновой функции представляет собой плотность вероятности обнаружить электрон в той или иной точке пространства. Если эта же волновая функция задана в импульсном представлении, то квадрат её модуля представляет собой плотность вероятности обнаружить тот или иной импульс.
Для волновых функций справедлив принцип суперпозиции.
Волновая функция в квантовой механике, величина, полностью описывающая состояние микрообъекта (например, электрона, протона, атома, молекулы) и вообще любой квантовой системы (например, кристалла).
Описание состояния микрообъекта с помощью волновой функции имеет статистический, т. е. вероятностный характер: квадрат абсолютного значения (модуля) волновая функция указывает значение вероятностей тех величин, от которых зависит волновой функции Например, если задана зависимость волновой функции частицы от координат х, у, z и времени t, то квадрат модуля этой волновой функции определяет вероятность обнаружить частицу в момент t в точке с координатами х, у, z. Поскольку вероятность состояния определяется квадратом Волновой функции, её называют также амплитудой вероятности.
Волновая функция одновременно отражает и наличие волновых свойств у микрообъектов. Так, для свободной частицы с заданным импульсом р и энергией E, которой сопоставляется волна де Бройля с частотой ω = E/ђ и длиной волны λ = ђ/p (где ђ — постоянная Планка), Волновая функция должна быть периодична в пространстве и времени с соответствующей величиной λ и периодом Т = 1/v.
Для волновой функции справедлив суперпозиций принцип: если система может находиться в различных состояниях с волновой функции ψ1, ψ2.., то возможно и состояние с Волновой функции, равной сумме (и вообще любой линейной комбинации) этих Волновая функция Сложение Волновой функции (амплитуд вероятностей), а не вероятностей (квадратов Волновой функции) принципиально отличает квантовую теорию от любой классической статистической теории (в которой справедлива теорема сложения вероятностей)[4].
Амплитуда рассеяния.
Амплитуда рассеяния в квантовой теории столкновений – величина, количественно описывающая столкновение микрочастиц.
Пучок падающих на мишень частиц (с определённым импульсом) рассеивается; при этом частицы могут отклониться в любом направлении. Относительное число частиц, вылетающих под разными углами к первоначальному направлению пучка, зависит от конкретного закона взаимодействия рассеиваемых частиц с частицами мишени. Вероятность рассеяния частицы под данным углом определяется амплитуда рассеяния.
Одна из основных количественных характеристик, как упругого рассеяния, так и неупругих процессов, — эффективное поперечное сечение процесса (называемое обычно просто сечением) — величина, пропорциональная вероятности процесса и имеющая размерность площади. Измерение сечений процессов позволяет изучать законы взаимодействия частиц, исследовать структуру частиц. Например, классическими опытами Э. Резерфорда по рассеянию a-частиц атомами было установлено существование атомных ядер (см. Резерфорда формула); из опытов по рассеянию электронов большой энергии на протонах и нейтронах (нуклонах) получают информацию о структуре нуклонов; эксперименты по упругому рассеянию нейтронов и протонов протонами позволяют детально исследовать ядерные силы и т.д [5].
Поляризация нейтронного пучка.
Если к нейтрону приложить электрическое поле E, то он слегка деформируется, поскольку к положительному и отрицательному составляющим его зарядам будут приложены противоположные силы. Возникнет наведенный электрический дипольный момент dα, причем его величина будет пропорциональна величине приложенного поля: dα = αn · E.
Здесь αn — так называемая электрическая поляризуемость нейтрона. Она характеризует "жесткость" нейтрона, т.е. его внутреннюю структуру. Ее удалось измерить только в 1991 году (группа Шмидмайера в Австрии). Оказалось αn = (1, 20 ± 0, 20) · 10-3 Фм3 , здесь использована единица длины: ферми (1 Фм = 10-13 см), которая имеет порядок размера нуклона. Такая поляризуемость соответствует возникновению наведенного ЭДМ dα ≈ 10-27 е·см, если к нейтрону приложить поле ≈ 108 В/см, которое соответствует по порядку величины межатомным полям в веществе и приблизительно в 103 раз превосходит поля, достижимые в лаборатории. Конечно, даже такая величина поля совершенно недостаточна, чтобы привести к какомулибо наблюдаемому эффекту. Гораздо более сильные электрические поля имеются вблизи поверхности атомного ядра, например, вблизи ядер свинца они могут достигать величин ≈ 1021 В/см. Именно эти поля и удалось использовать для измерения электрической поляризуемости нейтрона при рассеянии нейтронов на атомах свинца[2].
2.1 Получение выражения для амплитуды рассеяния нейтрона в ядерной среде.
Рассмотрим в виде таблицы как может осуществляться последовательный переход от движения сводного нейтрона к движению среди множества ядер.
Таблица 2.1.1 – Сравнительная характеристика волновых функций нейтрона в различных ситуациях
Мишень (ядро) |
ВФ нейтрона после рассеяния без учета спинов ВФ |
ВФ нейтрона после рассеяния с учетом спинов ВФ |
| отсутствие | ||
Ядро в точке
|
||
Ядро в точке
|
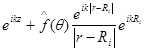 |
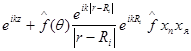 |
Множество ядер в точках
|
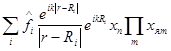 |
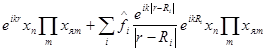 |
![]() - спиновая волновая функция ядер
- спиновая волновая функция ядер
P=<J>/J – вектор поляризации ядер
Таблица 2.1.2 сравнительная характеристика координатного и спинового усреднения волновой функции
| этап | 1 | 2 |
| По спиновому состоянию ядер | По координатам ядер (по пространственному положению) |
|
| Что происходит | Исчезает преумножение спинов ВФ, а амплитуда рассеивания примет вид
|
Исчезает ∑ по ядрам, а вместо нее появляется плотность |
| Конечная формула | 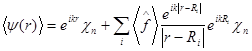 |
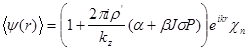 |
2.2 Существование 2 показателей преломления ядерной среды (спиновый дихроизм).
Если волна проходит слой поляризованного вещества конечной толщины, то для показателя преломления для неполяризованной мишени, получим, что показатель преломления нейтронов со спином, параллельным p,
![]()
(1)
Для нейтронов с противоположной поляризацией
![]() (2)
(2)
Разность
![]() (3)
(3)
определяется разностью соответствующих когерентных амплитуд рассеяния и отлична от нуля только в поляризованной среде.
Таким образом, в поляризованной ядерной мишени нейтроны обладают двумя показателями преломления.
2.3 Расчет зависимости поляризации от пройденного нейтронным пучком расстояния и зависимости угла поворота от расстояния.
Пусть на поляризованную среду падают нейтроны, вектор поляризации которых ориентирован под некоторым углом к направлению p. Такое состояние нейтрона можно рассматривать как суперпозицию двух состояний с поляризациями по вектору p и против него. Начальная волновая функция частицы тогда имеет вид
![]()
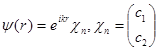 (4)
(4)
![]() (5)
(5)
Изучим преломление на мишени
![]() (6)
(6)
![]() (7)
(7)
Состояние типа ![]() обладает показателем преломления n+
, а состояние типа
обладает показателем преломления n+
, а состояние типа ![]() – показателем преломления n-
, то волновая функция нейтрона в поляризованной среде изменяется с глубиной следующим образом:
– показателем преломления n-
, то волновая функция нейтрона в поляризованной среде изменяется с глубиной следующим образом:
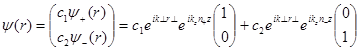 (8)
(8)
Используя это выражение, можно найти вектор поляризации нейтрона
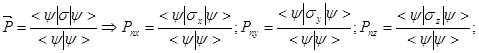 (9)
(9)
Тройка матриц Паули
![]()
![]() (10)
(10)
В результате получаем
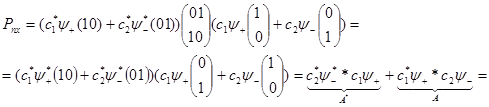 (11)
(11)
![]() (12)
(12)
![]() (13)
(13)
![]() (14)
(14)
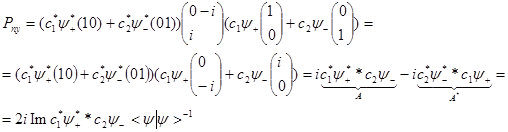 (15)
(15)
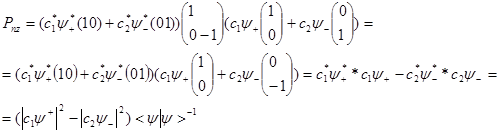 (16)
(16)
Предположим, что спин нейтронов в вакууме направлен перпендикулярно к вектору поляризации ядер. Выберем это направление в качестве оси X. В этом случае c1=c2=1/21/2
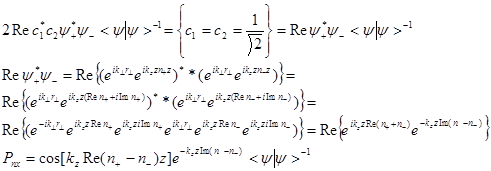 (17)
(17)
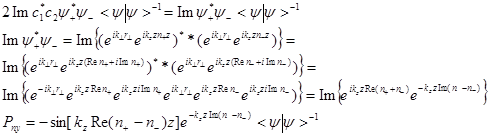 (18)
(18)
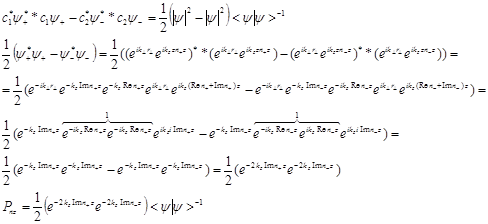 (19)
(19)
По мере прохождения в глубь мишени вектор поляризации нейтрона поворачивается вокруг направления вектора поляризации ядер на угол
![]() (20)
(20)
![]() (21)
(21)
И тогда получаем:
![]() (22)
(22)
2.4 Энергия нейтрона в ядерной среде. Зависимость от направления спина нейтрона по отношению к вектору поляризации ядер
По мере прохождения в глубь мишени с поляризованными ядрами вектор поляризации нейтрона поворачивается. С точки зрения кинематики это явление вполне аналогично магнитному вращению плоскости поляризации света (эффект Фарадея).
Вывод о вращении спина нейтрона в поляризованной мишени можно получить и из других соображений.
Вследствие того что в поляризованной ядерной мишени нейтронная волна обладает двумя показателями преломления, в такой мишени она обладает двумя возможными энергиями взаимодействия U+- (в зависимости от спинового состояния волны):
![]() (23)
(23)
или, аналогично в операторном виде
![]() (24)
(24)
2.5 Получение выражения для ядерного псевдомагнитного поля
Рассмотрим теперь движение нейтрона в магнитном поле H. В этом случае энергия взаимодействия W+ частицы с магнитным моментом, параллельным H , дается хорошо известным выражением W+ = -μ H (μ- магнитный момент нейтрона), а аналогичная величина для частицы с противоположным направлением спина – выражением W- =μH. Наличие отличной от нуля разности W+ - W- =-2μH приводит к ларморовской прецессии спина нейтрона в магнитном поле H с частотой [24]
![]() (25)
(25)
За время t спин повернется на угол υ = ωt. Если магнитное поле сосредоточено в слое толщиной l, то нейтрон, влетающий в область, занятую полем, под некоторым углом, пройдет этот слой за время t = l/√z. Следовательно, его спин повернется на угол
![]() (26)
(26)
что полностью совпадает с полученным ранее результатом.
Продолжая далее аналогично с магнитным полем, естественно для описания прецессии спина нейтрона, вызванной ядерным взаимодействием (ниже мы будем называть ее ядерной прецессией), ввести эффективное магнитное поле
![]() (27)
(27)
которое приводит к прецессии с той же частотой ω, что и обычное магнитное поле H . Отметим, что в области энергий нейтрона, в которой амплитуда рассеяния постоянна, частота ω также является постоянной, характеризующей вращательную способность вещества, обусловленную ядерным взаимодействием. Это имеет место для малых энергий нейтронов. При увеличении скорости частота прецессии спина начинает зависеть от энергии; в частности, вблизи каждого из резонансов частота резко возрастает, а при прохождении резонанса вследствие изменения знака реальной части амплитуды рассеяния изменяется знак. Напомним (см., например, [2,22]), что вблизи резонанса амплитуда рассеяния
![]() (28)
(28)
где E– энергия частицы; E0 – энергия резонанса; Г – ширина резонансного уровня. Вследствие соотношения (6,29) величина эффективного квазимагнитного поля ядерного происхождения в области низких энергий является постоянной, характеризующей данное вещество, а при более высоких энергиях зависит от энергии. Для поляризованной протонной мишени, например, в случае полной поляризации ω ≈ 5*108 с-1 , Hэф ≈ 3*104 Гс = 3 Тл и на два порядка превосходит обычное магнитное поле, создаваемое поляризованными магнитными моментами протонов. В этих же условиях для тепловых нейтронов u = 2,2*105 см*с-1 длина L, на которой произойдет полный поворот спина, равна L ≈ 10-3 см.
С учетом сказанного выше мы можем записать уравнение Шредингера для когерентной волны, взаимодействующей с поляризованной мишенью, помещенной в магнитном поле B:
![]() (29)
(29)
![]() (30)
(30)
где μ = μσ – оператор магнитного момента нейтрона. Заметим, что Ǔ(r) можно переписать следующим образом:
![]() (31)
(31)
где
![]()
эффективное квазимагнитное ядерное поле[1].
Заключение
Взаимодействие нейтронов с атомами является сравнительно слабым, что позволяет нейтронам достаточно глубоко проникать в вещество — в этом их существенное преимущество по сравнению с рентгеновскими и γ-лучами, а также пучками заряженных частиц. Из-за наличия массы нейтроны при том же импульсе (следовательно, при той же длине волны) обладают значительно меньшей энергией, чем рентгеновские и γ-лучи, и эта энергия оказывается сравнимой с энергией тепловых колебаний атомов и молекул в веществе, что дает возможность изучать не только усредненную статическую атомную структуру вещества, но и динамические процессы, в нем происходящие. Наличие магнитного момента у нейтронов дает уникальную возможность использовать их для изучения магнитной структуры и магнитных возбуждений вещества, что очень важно для понимания свойств и природы магнетизма материалов.
Рассеяние нейтронов атомами обусловлено, в основном, ядерными силами, следовательно, сечения их когерентного рассеяния никак не связаны со строением электронных оболочек атомов. Поэтому "освещение" материалов нейтронами позволяет различать положения атомов легких (водород, кислород и др.) элементов, идентификация которых почти невозможна с использованием рентгеновских и γ-лучей. По этой причине нейтроны успешно применяются при изучении биологических объектов, в материаловедении, в медицине и др. областях.
Список использованной литературы
1. В.Г. Барышевский. Ядерная оптика поляризованных сред. М.: Энергоатомиздат, 1995.-320с.
2. В.В. Федоров. Нейтронная физика. СПб.: изд-во ПИЯФ, 2004. 334стр.
3. И.В. Савельев. Курс общей физики. Том 3. М.: Наука, Гл. ред. физ-мат. лит., 1970.— 537с.
4. http://ru.wikipedia.org/wiki/Волновая_функция
5. http://slovari.yandex.ru/dict/bse/article/00002/79600.htm
6. http://mirslovarei.com/content_bes/Dixroizm-19067.html
Похожие работы
-
История первого ядерного реактора
Первый Ядерный реактор построен в декабре 1942 в США под руководством Э. Ферми. В Европе первый Ядерный реактор пущен в декабре 1946 в Москве под руководством И. В. Курчатова. К 1978 в мире работало уже около тысячи Ядерный реактор различных типов. Составными частями любого Ядерный реактор являются: активная зона с ядерным топливом, обычно окруженная отражателем нейтронов, теплоноситель, система регулирования цепной реакции, радиационная защита, система дистанционного управления (рис. 1).
-
Изотопы
Изото́пы (от греч. ισος — «равный», «одинаковый», и τόπος — «место») — разновидности атомов (и ядер) одного химического элемента с разным количеством нейтронов в ядре. Название связано с тем, что изотопы находятся в одном и том же месте (в одной клетке) таблицы Менделеева.
-
Атомная энергетика, атомные станции
Содержание: 1. Основы ядерной энергетики. 1 стр. 1.1 Способы получения энергии. 1 стр. 1.2 Способы организации реакции горения, цепные реакции 1 стр.
-
Ядерные реакторы и безопасность
ЯДЕРНЫЕ РЕАКТОРЫ И БЕЗОПАСНОСТЬ ВВЕДЕНИЕ.................................................................................................
-
Атомный реактор.
Введение Основным прикладным результатом фундаментальных исследований в ядерной физике явилось становление атомной энергетики. Производимая в ядерных реакторах энергия составляет около 6% всего мирового производства энергии. В некоторых странах ( Франция, Швеция ) атомные электростанции дают более половины всей электроэнергии.
-
Ядерная энергия
Д О К Л А Д п о ф и з и к е по теме "Термоядерный синтез" Введение В 1939 году впервые удалось расщепить атом урана. Прошло еще 3 года, и в США был создан реактор для осуществления управляемой ядерной реакции. Затем в 1945г. была изготовлена и испытана атомная бомба, а в 1954г. в нашей стране была пущена в эксплуатацию первая в мире атомная электростанция.
-
Ядерная физика
В современной физике есть год, который называют «годом чудес». Это 1932-й год. Одним из таких «чудес» этого года было открытие нейтрона и создание нейтронно-протонной модели
-
Опыт Резерфорда
ЕЗЕРФОРД Эрнст (1871-1937), английский физик, один из создателей учения о радиоактивности и строении атома, основатель научной школы, иностранный член-корреспондент РАН (1922) и почетный член АН СССР (1925). Директор Кавендишской лаборатории (с 1919). Открыл (1899) альфа- и бета-лучи и установил их природу.
-
Задача по Физике 2
№506 На тонкую пленку в направлении нормали к ее поверхности падает монохроматический свет с длиной волны = 500 нм. Отраженный от нее свет максимально усилен вследствие интерференции. Определить минимальную толщину dmin пленки, если показатель преломления материала пленки n = 1,4.
-
Использование достижений современной ядерной физики
Основное применение радионуклидов и радиоактивного излучения в химии. Характеристика методов радиоаналитической химии. Радиоуглеродный метод хронологической маркировки ископаемых находок органического происхождения. Ядерная физика в медицине и геологии.