Название: Визначення модуля пружності з деформації розтягу

Вид работы: лабораторная работа

Рубрика: Физика

Размер файла: 80.51 Kb

Скачать файл: referat.me-341503.docx

Краткое описание работы: Лабораторна робота № 2 ВИЗНАЧЕННЯ МОДУЛЯ ПРУЖНОСТІ З ДЕФОРМАЦІЇ РОЗТЯГУ Мета роботи: Дослідити залежність видовження зразка від навантаження. Визначити модуль Юнга для капрону.

Визначення модуля пружності з деформації розтягу

Лабораторна робота № 2

ВИЗНАЧЕННЯ МОДУЛЯ ПРУЖНОСТІ

З ДЕФОРМАЦІЇ РОЗТЯГУ

Мета роботи: Дослідити залежність видовження зразка від навантаження. Визначити модуль Юнга для капрону.

Прилади і матеріали: Прилад для визначення модуля пружності, рулетка, мікрометр, важки.

Теоретичні відомості

Деформацією називають зміну форми чи об’єму твердого тіла, яка викликана дією зовнішніх сил. Якщо ці сили малі, то після припинення їх дії деформація зникає; якщо ж сили великі, то після припинення дії виявляється так звана залишкова деформація . При появі щонайменшої залишкової деформації говорять, що досягнуто межу пружності .

Оскільки результат дії сили залежить також і від розмірів зразка, то зручно дію сили оцінювати по напрузі , що виникає в зразку.

Напругою називають відношення сили F до площі поперечного перерізу зразка S:

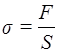
(1)

Таким чином, межа пружності s _пр – це напруга, при якій з’являється залишкова деформація. Тіла з великим значенням s _пр називають пружними , а тіла з дуже малим значенням s _пр – непружними або пластичними .

Серед різних деформацій виділяють дві найпростіші: деформаціюрозтягу (стиску ) і деформаціюзсуву . Всі малі деформації можна розглядати як суму деяких розтягів (чи стисків) і зсувів.

Малі деформації задовольняють таким основним законам :

- в межах пружності деформація пропорційна прикладеній напрузі;

- при зміні напряму дії зовнішньої сили змінюється тільки напрям деформації без зміни її значення;

- при дії декількох зовнішніх сил загальна деформація дорівнює сумі окремих деформацій (принцип суперпозиції малих деформацій).

Для малих деформацій розтягу чи стиску стержня справедливий закон Гука:

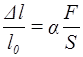,	(2)
або	(2´)

В (2) і (2´): l ₀ – початкова довжина стержня; D l = l – l ₀ – його абсолютне видовження; 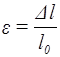називають відносним видовженням ; a – коефіцієнт пружності під час розтягу.

Величина, обернена a , називається модулем пружності під час розтягу, абомодулем Юнга :

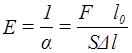
(3)

З використанням модуля Юнга закон Гука записують так:

(4)

Під дією сили F , що розтягує стержень, змінюються не тільки повздовжні, а й поперечні розміри стержня; говорять, що під час розтягу стержень зазнає поперечного стиску . Якщо d₀ – діаметр стержня до деформації, d – після деформації, то

,

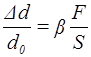(5)

де D d = d – d₀ , b – коефіцієнт поперечного стиску.

Відношення відносного поперечного стиску до відповідного відносного поздовжнього видовження (або відношення ) називають коефіцієнтом Пуассона : :.

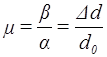Теоретично для всіх ізотропних тіл m =0,25 .

Опис установки

В установці (рис.1) використовується довга (близько 5 м) капронова нитка діаметром 0,2¸0,4 мм (рибальська волосінь). На малюнку вона позначена цифрою 1 . За допомогою блоків 2 капронова нитка закріплена на робочому столі. До кінця нитки приєднано платформу для важків 3 . Поруч вертикально закріплено лінійку 4 , на якій з допомогою покажчика 5 можна відмічати положення кінця нитки. Значна довжина нитки дає змогу вже при невеликих навантаженнях ( » 1Н ) з достатньою точністю виміряти абсолютне видовження D l . Модуль Юнга визначається за формулою (3) для різних значень F .

Хід роботи

1. Виміряйте рулеткою довжину капронової нитки l₀ до стрілки–покажчика 5 при ненавантаженій платформі. Допустима похибка вимірювання - 1 см.

2. Мікрометром виміряйте діаметр нитки d . Вимірювання виконайте декілька разів в різних місцях і знайдіть з одержаних значень середнє арифметичне.

3. Запишіть початкове положення стрілки–покажчика n₀ .

4. Навантажте платформу важком масою m . При обчисленні сили тяжіння F , що діє на цей важок, g брати рівним .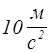

5. Запишіть положення стрілки n₁ .

6. Навантажуйте платформу послідовно важками, збільшуючи масу їх щоразу на m г. Записуйте кожного разу покази стрілки n₂ , n₃ , і т.д.

7. Максимальне навантаження уточніть у викладача.

8. Почніть розвантажувати платформу, знімаючи кожного разу теж по m г. Записуйте щоразу покази стрілки n ¢ ₆ , n ¢ ₅ , n ¢ ₄ і т.д. до n ₀ .

9. Побудуйте графік зміни видовження нитки зі зміною навантаження F : при F₁ D l₁ = n₁ – n₀

приF₂ D l₂ = n₂ – n₀ і т.д.

10.Проаналізуйте одержаний графік. Чи виконується закон Гука?

11.Обчисліть для кожного видовження модуль Юнга за формулою:

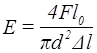(6)

В (6) враховано, що площа .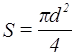

12.Знайдіть середнє арифметичне з одержаних значень Е і порівняйте з табличним.

13.Результати вимірювань і обчислень можна подати у вигляді таблиці 1. Похибка вимірювань:

14.Кінцевий результат подати у виді ,

де .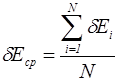

Табл.1

№ п/п	F = mg, Н	l0 , м	d, м	D l, м	E,	d E
1
2
3
.
.
Середнє	–	–

Контрольні запитання

1. Які деформації називають пружними?

2. Сформулюйте закон Гука.

3. Який фізичний зміст модуля Юнга?

4. Що називають коефіцієнтом Пуассона?

5. Накресліть діаграму розтягу дроту і поясніть фізичний смисл окремих її ділянок.

6. Яку довжину повинен мати мідний дріт, щоб він, якщо його підвісити вертикально, розірвався під дією власної ваги?