Название: Определение момента инерции твердых тел

Вид работы: лабораторная работа

Рубрика: Физика

Размер файла: 78.76 Kb

Скачать файл: referat.me-341517.docx

Краткое описание работы: Федеральное Агентство по образованию ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР) Кафедра физики ОТЧЕТ Лабораторная работа по курсу "Общая физика"

Определение момента инерции твердых тел

Федеральное Агентство по образованию

ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР)

Кафедра физики

ОТЧЕТ

Лабораторная работа по курсу "Общая физика"

ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ ТВЕРДЫХ ТЕЛ

Выполнил: студент группы

Проверил:

2009 г.

1. ЦЕЛЬ РАБОТЫ

Целью настоящей работы является изучение основных законов динамики поступательного и вращательного движений твердых тел, экспериментальное определение момента инерции блока и сравнение его с расчетным значением.

2. ОПИСАНИЕ УСТАНОВКИ И МЕТОДИКИ ЭКСПЕРИМЕНТА

Схема экспериментальной установки на основе машины Атвуда приведена на рис. 2.1.

На вертикальной стойке 1 крепится массивный блок 2, через который перекинута нить 3 с грузами 4 одинаковой массы, равной 80 г. В верхней части стойки расположен электромагнит, который может удерживать блок, не давая ему вращаться. На среднем кронштейне 5 закреплен фотодатчик 6. Риска на корпусе среднего кронштейна совпадает с оптической осью фотодатчика. Средний кронштейн имеет возможность свободного перемещения и фиксации на вертикальной стойке. На стойке укреплена миллиметровая линейка 7, по которой определяют начальное и конечное положение грузов. За начальное, принимают положение нижнего среза груза, за конечное - риску на корпусе среднего кронштейна.

Миллисекундомер 8 представляет собой прибор с цифровой индикацией времени. Опоры 9 используют для регулировки положения установки на лабораторном столе.

Принцип работы машины Атвуда заключается в следующем. Когда на концах нити висят грузы одинаковой массы, система находится в положении безразличного равновесия. Если же на один из грузов (обычно на правый) положить перегрузок, то система выйдет из равновесия, и грузы начнут двигаться с ускорением.

Машина Атвуд а

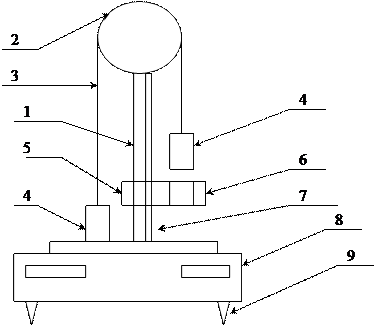
1 – стойка;

2 – блок;

3 – нить;

4 – грузы;

5 – средний кронштейн;

6 – фотодатчик;

7 – линейка;

8 – миллисекундомер;

9 – регулировочная опора.

Рис. 2.1

3. ОСНОВНЫЕ РАСЧЕТНЫЕ ФОРМУЛЫ

Средние значение времени <t > и средние значение квадрата времени < t ² > прохождения грузом с перегрузкомпутиh :

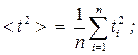
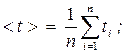
(3.1), (3.2)

Абсолютная суммарная погрешность измерения времени прохождения пути h :

(3.3)

Абсолютная случайная погрешность измерения времени прохождения пути h :

σ_сл (t ) = t(a, n ) ×S (t ) ; (3.4)

где t(a, n ) - коэффициент Стьюдента

стандартная абсолютная погрешность измерения времени:

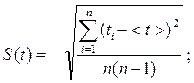
(3.5)

где t_i − время прохождения пути при i –ом измерении ( i =1. … , n );

n – число измерений;

< t > – среднее значение времени прохождения пути.

Абсолютная суммарная погрешность косвенного измерения квадрата времени прохождения путиh :

σ(t ² ) = 2 < t > σ(t ) (3.6)

Исследуемая зависимость двух величин t ² и h является линейной , то есть удовлетворяет в общем виде формуле:

(3.7)

где k - константа, зависящая от параметров экспериментальной

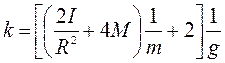установки:

(3.8)

где I − его момент инерции блока ;

R – радиус блока ;

M , m – масса груза и перегрузка ;

g – ускорение свободного падения.

4. РЕЗУЛЬТАТЫ РАБОТЫ И ИХ АНАЛИЗ.

Результаты измерений времени прохождения груза

(Таблица 4.1)

Номер измерения	h1 =28,0 см	h2 =22,0 см	h3 =18,0 см	h4 =12,0 см	h5 =8,0 см
1	3,617	3,281	3,092	2,348	1,986
2	3,73	3,23	2,891	2,346	1,921
3	3,797	3,414	3,133	2,521	2,099
4	3,597	3,414	3,061	2,323	2,058
5	3,837	3,238	2,882	2,412	2,096
	3,716	3,315	3,012	2,39	2,032
	13,815	10,999	9,082	5,717	4,134

Из таблицы методического указания к лабораторному практикуму по физике А.Г. Риппа определим коэффициент Стьюдента.

t(a, n ) = 2,1

Расчет погрешностей для построения графиков при коэффициенте

Стьюдента = 2,1

(Таблица 4.2)

Номер серии опытов	Среднеквадра-тичное отклонение , с	Случайная погрешность , с	Абсолютная погрешность , с	Погрешность вычисления , с2
1	0,05	0,11	0,11	13,815 ± 0,8
2	0,04	0,08	0,08	10,999 ± 0,5
3	0,05	0,11	0,11	9,082 ± 0,7
4	0,04	0,08	0,08	5,717 ± 0,4
5	0,04	0,08	0,08	4,134 ± 0,3

Определяем абсолютную систематическую приборную погрешность измерения времени согласно методическому указанию к лабораторному практикуму по физике А.Г. Риппа

с.

Построение графиков.

Метод наименьших квадратов для построения прямых по экспериментальным точкам :

где обозначено:

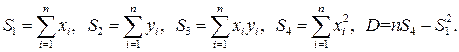
k= 0,49 с² /м угловой коэффициент прямой

b= 0,06 с² отрезок, отсекаемый прямой от оси OY

Искомая зависимость имеет вид: t ² = 0,49∙ h , с² (4.1)

Вычислим значения ординат прямой линии для двух контрольных точек при произвольных значениях h по выражению 4.1:

h ₀₁ = 15 см, t ² ₀₁ = 0,49×15= 7,35 c² → точка A ₀₁

h ₀₂ = 29 см, t ² ₀₂ = 0,49×29=14,21 c² → точка A ₀₂

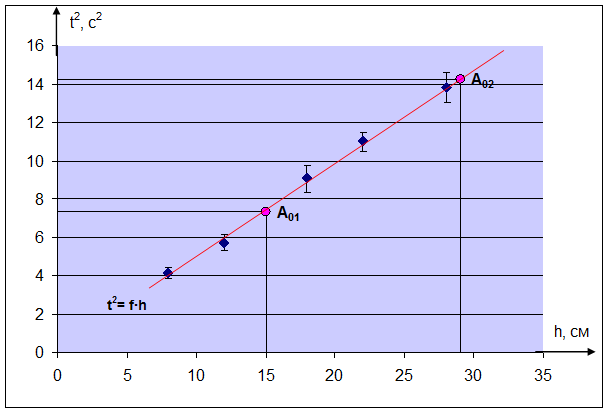
Рисунок 4.1. Зависимость квадрата времени t ² от пройденного пути h

Погрешности косвенного измерения параметров прямой линии k и b методом наименьших квадратов определяются по следующим формулам:

где

∆(k) ≈ 0,01 с² /м

∆(b) = 0,17 с²

Используя выражение (3.7) для и учитывая, что г, г, R = 75*10^-3 и g=980,67 см/с² вычисляется момент инерции блока.

I_ex = 16986 г∙см²

Абсолютная погрешности косвенного определения момента инерции блока I _э в ходе эксперимента, по формуле:

∆(I_ex) = 552 г∙см²

Экспериментальное значение момента инерции блока:

I__ex = (16986 ± 552) г∙см² = (1,7 ± 0,6) × 10 ^-4 кг∙м²

Используя геометрические параметры блока, с учетом плотности металла, из которого изготовлен блок (латунь, r = 8400 кг/м³ ), рассчитать его момент инерции.

Толщина блока в метрах d= 6∙10^-3 м

Объём сплошного диска V_CD= π∙d∙R²

V_CD= 1,06 см³

Масса сплошного диска m_CD= p∙ V_CD

m_CD = 890 г = 0,89 кг

Момент инерции сплошного диска I_CD= 1/2∙ m_CD∙r₂ ²

I_CD = 25031 г∙см²

Так как оси, проходящие через центры масс вырезанных дисков, не совпадают с осью вращения всего блока, то момент инерции I_can каждого диска находится по теореме Штейнера.

Радиус каждого выреза в метрах r₂ = 30∙10^{-3 м}

Объём каждого выреза V_can= π∙d∙ r₂ ²

V_can= 1.696∙10^-5 см³

Масса каждого вырезанного диска m_can= p∙V_can

m_can=142 г = 0,142 кг

Момент инерции каждого вырезанного диска относительно его центра масс:

Ic=1/2∙m_can∙ r₂ ² Ic = 639 г∙см²

r₁ =40∙10^-3 м расстояние от оси вращения блока до центра масс каждого

вырезанного диска в метрах

Момент инерции каждого вырезанного диска относительно оси вращения блока:

I_can=Ic+ m_can∙ r₁ ² I_can = 639 г∙см²

Момент инерции цилиндрического отверстияI _отв относительно оси, проходящей через центр масс блока, определяем по формуле:

= 2911 г∙см²

Момент инерции блока с тремя вырезами в виде малых дисков

I_an= I_CD-3∙ I_can I_an = 16298 г∙см²

Полученные экспериментальным и аналитическим способами моменты инерции можно сравнить, получив отличие между ними в процентах, при помощи нижеследующего соотношения:

5. ВЫВОДЫ

Используя экспериментальные данные, был построен график линеаризованной зависимости и рассчитаны коэффициенты соответствующего уравнения t ² = f ( h ) = 0,49∙ h с² . Все точкив этой зависимостиукладываются на прямую в пределах их погрешностей.Это свидетельствует, что экспериментальная зависимость t ² = f ( h ) соответствует теоретической, т.е. экспериментально доказана справедливость основного уравнения динамики вращательного движения:

Значение собственного момента инерции,полученное в ходе эксперимента равно:

I_ex = 1,7 кг∙м²

Используя геометрические параметры блока, с учетом плотности металла, из которого изготовлен блок, рассчитан его момент инерции:

I_an = 1,6кг∙м²

Значение собственного момента инерции,полученное в ходе эксперимента, больше расчетного

Несовпадение экспериментального результата с расчетным можно объяснить тем, что не учитывался момент сил трения. Это и привело к завышенному значению собственного момента инерции блока в эксперименте.

6. ОТВЕТЫ НА КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Что такое момент сил и момент инерции?

Моментом силы относительно оси называется физическая величина, численно равная произведению величины составляющей силы, действующей в плоскости, перпендикулярной оси вращения, на плечо этой составляющей, т.е. на кратчайшее расстояниеr от оси вращения до линии действия

Момент силы относительно оси есть вектор, направленный вдоль этой оси и связан с направлением вращения правилом правого винта.

Момент инерции характеризует инерционные свойства вращающихся тел. Чем больше момент инерции тела, тем труднее изменить его угловую скорость. Момент инерции во вращательном движении аналогичен массе тела в поступательном движении. Момент инерции тела относительно некоторой оси зависит от распределения его массы относительно оси вращения.

Для элемента тела массой dm момент инерции dI выражается соотношением: dI = r ² dm ,

где r – расстояние от элемента dm до оси вращения.

Момент инерции всего тела запишется в виде интеграла

где интегрирование осуществляется по всему телу.

2. Моменты каких сил действуют на блок?

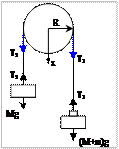Т₁ и Т₂ – силы натяжения нитей.

На блок действуют моменты сил натяжения нитей:

M ₁ = T ₁ R , M ₂ = T ₂ R .

Вращательное движение блока описывается уравнением:

Рис. 6.1

где ε - угловое ускорение блока, I - его момент инерции,

- сумма моментов сил, приложенных к блоку.

Согласно рис.6.1 вращательное движение блока описывается уравнением

3. Как рассчитать момент инерции блока?

Сформулировать теорему Штейнера.

Момент инерции блока рассчитывается как:

I = I _диск – 3× I _отв

где I _диск – момент инерции сплошного диска;

I _отв – момент инерции цилиндрического отверстия (“дырки”).

Момент инерции цилиндрического отверстияI _отв относительно оси, проходящей через центр масс блока, определяем согласно теоремы Штейнера.

Теорема Штейнера :

Момент инерции I относительно произвольной оси, равен сумме момента инерции I ₀ относительно оси, параллельной данной и проходящей через центр масс тела и произведения массы тела m на квадрат расстояния l между осями:

I = I ₀ + ml ²

4. Укажите возможные причины несовпадения экспериментальных результатов с расчетными.

Физические допущения, принятые при теоретическом анализе движения грузов в эксперименте; погрешности измерения величин; точность вычислений.

7. ПРИЛОЖЕНИЕ

К работе прилагается:

· регистрационный файл - phyLab2.reg

· файл журнала измерений - Ж.лаб2.txt