Название: Электронные цепи СВЧ (конспект) Add1
Вид работы: реферат
Рубрика: Физика
Размер файла: 100.51 Kb
Скачать файл: referat.me-341649.docx
Краткое описание работы: Параметры матрицы рассеяния могут быть рассчитаны по известной матрице проводимости четырехполюсника по формуле: – единичная матрица. Необходимо отметить важную особенность параметров матрицы рассеяния, связанную с направлением прохождения сигнала. При изменении направления передачи изменятся лишь индексы в параметрах рассеяния (
Электронные цепи СВЧ (конспект) Add1
Параметры матрицы рассеяния могут быть рассчитаны по известной матрице проводимости четырехполюсника по формуле:
![]() ,
,
где ![]() – единичная матрица.
– единичная матрица.
Необходимо отметить важную особенность параметров матрицы рассеяния, связанную с направлением прохождения сигнала. При изменении направления передачи изменятся лишь индексы в параметрах рассеяния (![]() на
на ![]() ,
, ![]() на
на ![]() ), знаки же величин, входящих в уравнения (3.1) останутся прежними.
), знаки же величин, входящих в уравнения (3.1) останутся прежними.
Установим связь между параметрами волновой теории (S -матрицей) и параметрами классической теории (Y -матрицей). Для этого рассмотрим четырехполюсники с направлениями падающих и отраженных волн, а также токов и напряжений, как показано на рисунках, и, соответствующие данным системам параметров, уравнения:

Рис. 3.2 Четырехполюсники в системе волновой и классической теорий
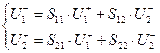 |
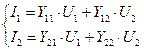 |
Учитывая введенные ранее обозначения для падающих и отраженных волн
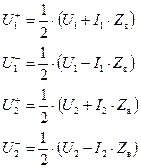 ,
,
а также выразив из этих уравнений токи и напряжения, подставим их в уравнения для S -параметров:
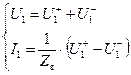
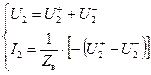 .
.
(минус, так как ток ![]() направлен из четырехполюсника).
направлен из четырехполюсника).

Рис. 3.3 К расчету S-матрицы по матрице Y
Подставляя в уравнения для ![]() параметров, получим:
параметров, получим:
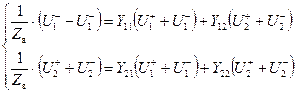 .
.
Приведем к общему знаменателю:
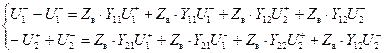 .
.
Перегруппируем слагаемые
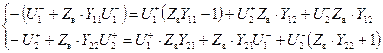 .
.
и выразим из полученных уравнений падающие и отраженные волны:
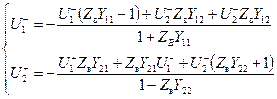 .
.
Далее учтем нормировку матрицы проводимости: ![]() .
.
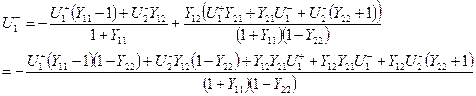 .
.
Первое уравнение получим в виде:
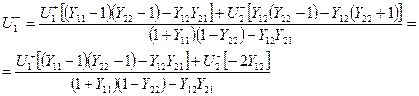 .
.
Преобразуем второе уравнение:
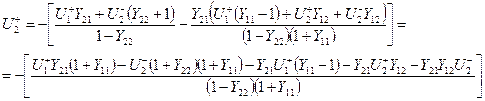 .
.
Получим:
![]()
Матрица коэффициентов полученной системы запишется:
![]()
.
Волновая матрица передачи . Если в качестве зависимых переменных выбрать волны на входе четырехполюсника – волну падающую на вход и волну отраженную от входа, а в качестве независимых переменных – волны на выходе - распространяющуюся к нагрузке и отраженную от нагрузки, то система уравнений, коэффициентами в которой будут параметры волновой матрицы передачи, запишется:
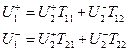
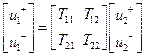 . (3.2)
. (3.2)

Описание четырехполюсников в виде волновой матрицы передачи удобно при их каскадном соединении. Результирующая матрица передачи в этом случае определится по соотношению:
![]() .
.
Где k -количество каскадно соединенных четырехполюсников.
Можно показать, что для взаимных четырехполюсников справедливо соотношение ![]() , а для симметричных:
, а для симметричных: ![]() .
.
Связь между волновой матрицей и матрицей классической теории Y устанавливают соотношения:
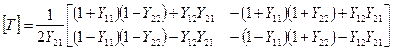 .
.
3.3. Расчет схемных функций по матрице передачи
Рассчитаем входной и выходной импедансы четырехполюсника, а также коэффициент передачи напряжения при произвольных нагрузках на входе и на выходе по А-матрице (или ABCD-матрице, как принято обозначать в зарубежных источниках) в соответствии с принятыми на рисунке обозначениями.
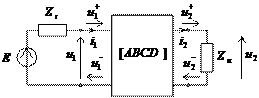
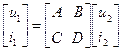
![]() . (3.3)
. (3.3)
Определим сопротивления нагрузки и генератора:
![]() ;
; ![]() .
(3.4)
.
(3.4)
Входное сопротивление определится в результате деления первого уравнения исходной системы на второе:
![]() .
.
Физический смысл параметров А -матрицы передачи:
![]() - обратный коэффициент передачи напряжения;
- обратный коэффициент передачи напряжения;
![]() - сопротивление передачи;
- сопротивление передачи;
![]() - проводимость передачи;
- проводимость передачи;
![]() - обратный коэффициент передачи тока.
- обратный коэффициент передачи тока.
Коэффициент передачи по напряжению от источника к нагрузке найдем, подставляя входное напряжение из (3.4), а затем входной ток из второго уравнения - в первое уравнение системы (3.3):
![]() .
.
Для вывода выражения для схемной функции ![]() рассмотрим четырехполюсник с независимым источником напряжения на выходе:
рассмотрим четырехполюсник с независимым источником напряжения на выходе:

Поставив в систему уравнений (3.3) входной и выходной токи с учетом знаков, получим:
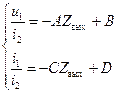 , выражая
, выражая ![]()
из первого уравнения и подставляя во второе – получим:
![]()
![]()
![]() .
.
Коэффициент отражения от входа:
![]() .
.
Коэффициент отражения от выхода:
![]() .
.
3.4. Связь между системами волновых параметров
1. Связь между волновыми матрицами устанавливается соотношениями:
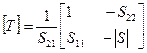
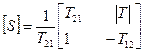 ,
,
где 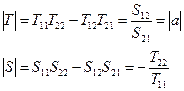 .
.
Матрицы существуют, если ![]() .
.
2. Связь между матрицами волновой и классической теорий:
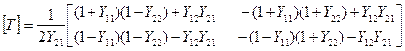 ;
;
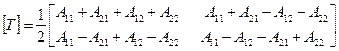 ;
;
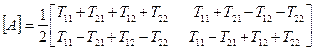 .
.
Похожие работы
-
Расчет линейной электрической цепи
Оглавление Введение 1. Задание 2. Определение комплексного коэффициента передачи напряжения; расчет и построение графиков АЧХ и ФЧХ 4. Определение параметров электрической цепи как четырехполюсника для средней частоты
-
Расчет линейной электрической цепи при гармоническом воздействии
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ Воронежский государственный технический университет Кафедра радиотехники Курсовая работа по курсу: «Общая электротехника и электроника»
-
Методы расчета установившихся режимов электроэнергетических систем
Получение оптимальной сети по критерию минимальных издержек на передачу активной мощности, исходя из матрицы удельных затрат. Расчет установившегося режима по полученной схеме. Суммарное распределение нагрузки системы методом приведенного градиента.
-
Сплавы магнитных переходных металлов
В последние годы интенсивно изучали электронную структуру и разнообразие физических свойств сплавов переходных металлов. Для изучения магнитных свойств сплавов переходных металлов очень полезным оказался метод рассеяния медленных нейтронов. Исследование упругого и неупругого рассеяния медленных нейтронов в сплавах позволяет получить уникальную информацию о магнитных моментах и форм-факторах, а также об изменении спин-волновой жесткости.
-
Исследование магнитной жидкости методом рассеяния света
Спектральные измерения интенсивности света. Исследование рассеяния света в магнитных коллоидах феррита кобальта и магнетита в керосине. Кривые уменьшения интенсивности рассеянного света со временем после выключения электрического и магнитного полей.
-
Расчет электрической цепи постоянного тока
Задание на выполнение работы Схема исследуемой цепи: Рис. 1. Принципиальная схема исследуемой цепи Таблица 1. Параметры элементов схемы Элемент схемы
-
Разработка сменного модуля для изучения резистивного соединения типа Треугольник
КУРСОВАЯ РАБОТА на тему: «Разработка сменного модуля для изучения резистивного соединения типа «Треугольник»» Содержание Введение 1. Теоретическая часть
-
Разработка сменного модуля для изучения соединения типа "Звезда"
Особенности соединения типа "звезда", порядок проектирования и изготовления сменного модуля для проведения лабораторных работ по его изучению. Понятие четырехполюсников и порядок определения режимов их работы, методика расчета специальных коэффициентов.
-
Расчет установившегося режима работы электрической системы
Определение параметров схемы замещения электрической системы. Формирование матрицы узловых проводимостей. Схемы замещения элементов электрической системы и ее расчет. Диагональная матрица проводимостей ветвей. Нелинейные уравнения установившегося режима.
-
Кристаллографические символы
Система обозначения граней и направлений. Индексы граней и ребер кристаллов. Символы ребер. Основные кристаллографические соотношения. Углы между двумя направлениями, между направлением и плоскостью. Межплоскостное расстояние и индексы плоскости.