Название: Исследование потока жидкости в канале переменного сечения

Вид работы: реферат

Рубрика: Физика

Размер файла: 74.51 Kb

Скачать файл: referat.me-341798.docx

Краткое описание работы: Анализ и особенности распределения поверхностных сил по поверхности жидкости. Общая характеристика уравнения Бернулли, его графическое изображение для потока реальной жидкости. Относительные уравнение гидростатики как частный случай уравнения Бернулли.

Исследование потока жидкости в канале переменного сечения

Реферат

на тему:

Исследование потока жидкости в канале переменного сечения.

Движение жидкости, в общем случае, обусловлено действием массовых сил.

Массовые силы непрерывно распределены по объему (массе) жидкости. К ним относятся сила тяжести и силы инерции переносного движения. Сила инерции переносного движения действует при ускоренном движении сосудов и каналов, содержащих жидкость. При этом относительно стенок сосудов или каналов жидкость может находиться в покое или двигаться с некоторой скоростью. Величина массовой силы пропорциональна массе жидкости или, для однородной жидкости, ее объему.

Поверхностные силы непрерывно распределены по поверхности жидкости и пропорциональны площади этой поверхности. Эти силы обусловлены непосредственным воздействием соседних объемов жидкости на рассматриваемый объем или же воздействием других тел (твердых или газообразных), соприкасающихся с рассматриваемым объектом. Поверхностные силы разделяют на силы давления и силы трения. Силы давления направлены по нормали поверхности жидкости, силы трения – по касательной к этой поверхности.

Установившееся (стационарное) движение жидкости, на которую действует из массовых сил только сила тяжести, описывается уравнением Бернулли. Для элементарной струйки идеальной жидкости уравнение Бернулли может быть получено на основе второго закона Ньютона, записанного для произвольного элементарного объема жидкости, и имеет вид:

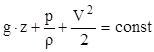(1)

Каждый член этого уравнения представляет собой удельную энергию, отнесенную к единице массы жидкости:

- удельная потенциальная энергия положения;

- удельная потенциальная энергия давления;

- удельная кинетическая энергия.

Если все члены уравнения (1) поделить на ускорение силы тяжести g, то получится другая формула записи уравнения Бернулли:

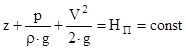(2)

Члены уравнения (2) так же представляют различные виды механической энергии жидкости, отнесенные к ее единице веса. Все слагаемые этого уравнения имеют размерность длины и носят название «высота» или «напор»:

- геометрическая высота (напор);

- пьезометрическая высота (напор);

- скоростная высота (напор);

- потенциальный или статический напор;

- полный гидродинамический напор.

Если все члены уравнения (1) умножить на плотность жидкости ρ, уравнение Бернулли принимает вид:

(3)

Члены этого уравнения имеют размерность давления (Па) и носят названия:

- весовое давление;

- гидродинамическое давление;

- динамическое давление;

Слагаемые уравнения (3) представляют различные виды механической энергии жидкости, отнесенные к единице ее объема. Таким образом, уравнение Бернулли в форме (1), (2), (3) описывает движение жидкости в поле силы тяжести и выражает закон сохранения полной удельной (т.е. отнесенной к единице массы, объема или веса) механической энергии жидкости.

Движение реальной (вязкой) жидкости сопровождается потерями энергии (напора) на трение и вихреобразование. Основываясь на законе сохранения энергии, для двух сечений потока реальной жидкости можно записать:

,

где - суммарные потери полного напора на участке между рассматриваемыми сечениями 1-1 и 2-2 (рис. 1)

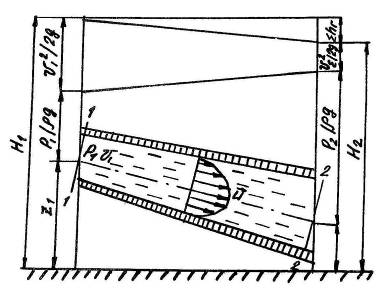
Рис. 1

Кроме того, при движении вязкой жидкости в поперечном сечении потока формируется неравномерный профиль скоростей. Наибольшего значения скорость достигает в центральной части потока , а по мере приближения к стенке она уменьшается до нуля.

Учет этих особенностей течения реальной жидкости приводит к следующему виду уравнения Бернулли:

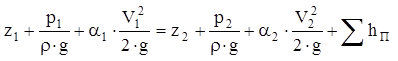(4)

Уравнение (4) называется уравнением Бернулли для потока реальной (вязкой) жидкости. В этом уравнении:

V1 и V2 – средние по сечению скорости потока;

α1 и α2 – коэффициенты Кориолиса, учитывающие неравномерность распределения скоростей в поперечном сечении потока. В ламинарных потоках α = 2, в турбулентных обычно при проведении расчетов полагают α = 1…1,04.

Графическое изображение уравнения Бернулли для потока реальной жидкости представлено на рис. 1.

Для экспериментальной проверки уравнения Бернулли необходимо провести измерение параметров потока жидкости в различных сечениях канала. Статическое давление измеряется при помощи пьезометра А, присоединенного к насадку. Срез приемного отверстия насадка располагается параллельно линиям тока в сечении, где производится измерение (рис. 2).

Возьмем в качестве одного из сечений сечение, совпадающее с плоскостью среза приемного отверстия насадка. В качестве второго сечения выберем поверхность, совпадающую с поверхностью уровня в пьезометре.

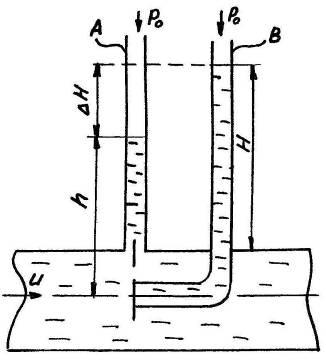
Рис.2

Для выбранных сечений запишем уравнение Бернулли с учетом того, что жидкость в пьезометре неподвижна:

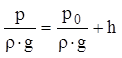,(5)

где h - высота подъема жидкости в пьезометре, p0 - атмосферное давление; p - абсолютное давление жидкости на уровне присоединения пьезометра.

Из уравнения (5):

(6)

Последнее уравнение называется относительным уравнением гидростатики. Это уравнение описывает равновесие жидкости в поле тяжести и является частным случаем уравнения Бернулли.

Рассмотрим трубку В (трубку полного напора), изогнутую под углом 90о отверстием навстречу потоку. Жидкость в этой трубке поднимается на большую высоту H > h.

Запишем уравнение Бернулли для сечения, взятого на некотором расстоянии от приемного отверстия (там где скорость потока ) и сечения, плоскость которого совпадает с плоскостью приемного отверстия:

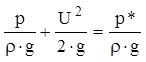,(7)

где - давление в плоскости приемного отверстия трубки полного напора, которое называется давлением заторможенного потока или полным давлением.

Из последнего уравнения

,

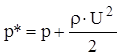т.е. полное давление больше статического на величину динамического давления .

Учитывая, что полное давление уравновешивается высотой столба жидкости Н, т.е.

,

из (7) получаем, что скорость потока в точке замера полного давления:

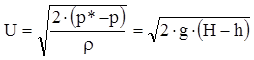(8)

Прибор, конструкция которого схематично показана на рисунке 2 носит название трубки полного давления или трубки Пито и применяется для измерения скорости движения жидкости.