Название: Полиномы Лагерра в квантовой механике
Вид работы: реферат
Рубрика: Физика
Размер файла: 888.53 Kb
Скачать файл: referat.me-341991.docx
Краткое описание работы: Министерство образования Российской Федерации Иркутский Государственный Технический Университет Физико-технический институт Кафедра Квантовой физики и нанотехнологий
Полиномы Лагерра в квантовой механике
Министерство образования Российской Федерации
Иркутский Государственный Технический Университет
Физико-технический институт
Кафедра Квантовой физики и нанотехнологий
КУРСОВАЯ РАБОТА
Тема:
Полиномы.
Полиномы Лагерра в квантовой механике
Выполнил (а) студент (ка)
2 курса, группы НТ-08,
.
Научный руководитель
.,ДФМН, профессор кафедры квантовой физики
Иркутск
2010
Содержание
Введение 3
Глава I . Ортогональные полиномы. 4
1.1. Понятие ортогональных полиномов 4
1.2. Классические ортогональные полиномы 5
1.3. Общие свойства ортогональных полиномов 7
Глава II . Полиномы Лагерра 8
Глава III . Применение полиномов Лагерра в квантовой механике 10
3.1. В радиальной части решения уравнения Шредингера для атома с одним электроном. 10
3.2. Переход в осцилляторе 12
Заключение 13
Используемая литература 14
Приложение 15
Введение
В представленной работе, я рассмотрела виды полиномов, в частности полиномы Лагерра, их основные свойства и применение в квантовой механике через математические выкладки решений уравнений Шредингера для атома водорода и гармонического осциллятора.
По своей сути полином - это алгебраическая сумма конечного числа одночленов, т.е. выражений вида Axk yl ...wm где x, y, ..., w -переменные, А (коэффициент многочлена) и k, l, ..., m (показатели степеней - целые неотрицательные числа)- постоянные. Многочлен от одного переменного x всегда можно записать в виде а0 хn + а1 хn -1 + ... + аn -1 х + аn .
К классическим ортогональным полиномам относятся полиномы Якоби![]() , Эрмита
, Эрмита![]() , Лагерра
, Лагерра ![]()
Они часто встречаются в теоретической и математической физике. Классические ортогональные полиномы удовлетворяют уравнениям вида
![]()
где -![]() полином степени не выше 2,
полином степени не выше 2, ![]() - полином степени не выше 1,
- полином степени не выше 1, ![]() - постоянная.
- постоянная.
В ходе работы использовала учебник Никифорова А.Ф.,Специальные функции математической физики; Фока. Начало квантовой механики.
Глава I . Ортогональные полиномы
1.1.Понятие ортогональных полиномов
Ортогональные полиномы
- системы полиномов ![]() , n = 0, 1, ...,
, n = 0, 1, ..., ![]() ортогональных с весом на интервале (а, b)
ортогональных с весом на интервале (а, b)
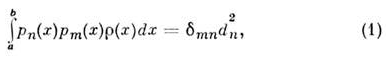
где - ![]() квадрат нормы. Подобные системы возникают в различных задачах математики, физики: в теории представлений групп, в вычислит. математике, при решении задач на собственные значения в теории волн, квантовой механике и др.
квадрат нормы. Подобные системы возникают в различных задачах математики, физики: в теории представлений групп, в вычислит. математике, при решении задач на собственные значения в теории волн, квантовой механике и др.
Задание веса![]() и интервала (а,b) определяет полином рn
(х), удовлетворяющий соотношению ортогональности (1) однозначно, с точностью до нормировочного множителя. Для полиномов рn
(х)справедливо след. явное выражение в виде определителя:
и интервала (а,b) определяет полином рn
(х), удовлетворяющий соотношению ортогональности (1) однозначно, с точностью до нормировочного множителя. Для полиномов рn
(х)справедливо след. явное выражение в виде определителя:
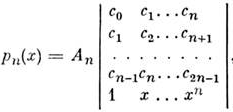
где Аn
- нормировочная постоянная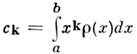 ,
,![]() - момент весовой функции. Из соотношений ортогональности (1) можно получить свойства Ортогональных полиномов.
- момент весовой функции. Из соотношений ортогональности (1) можно получить свойства Ортогональных полиномов.
1.2.Классические ортогональные полиномы.
Полиномы Якоби, Лагерра и Эрмита
– полиномы типа yn
(z) являются решениями уравнения ![]() . Явные выражения для этих полиномов даются формулой Родрига
. Явные выражения для этих полиномов даются формулой Родрига ![]() , где Bn
– нормировочная постоянная, а функция p(z) удовлетворяет дифференциальному уравнению
, где Bn
– нормировочная постоянная, а функция p(z) удовлетворяет дифференциальному уравнению ![]() .
.
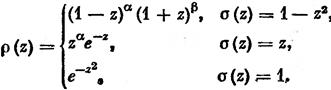 Решая эти уравнения, получим в зависимости от степени полинома
Решая эти уравнения, получим в зависимости от степени полинома ![]() следующие возможные виды функции p(z):
следующие возможные виды функции p(z):
где – ![]() некоторые постоянные.
некоторые постоянные.
![]() В зависимости от вида функции
В зависимости от вида функции ![]() получаются следующие системы полиномов:
получаются следующие системы полиномов:
1.Пусть
Тогда![]()
Соответствующие полиномы yn
(z) при ![]() называются полиномами Якоби и обозначаются
называются полиномами Якоби и обозначаются ![]()
![]()
2.Пусть ![]() Тогда
Тогда![]()
Полиномы yn
(z) при ![]() называются полиномами
называются полиномами
![]() Эрмита и обозначаются
Эрмита и обозначаются
![]()
3.Пусть![]() Тогда
Тогда![]()
![]() Полиномы yn
(z) при
Полиномы yn
(z) при ![]() называются полиномами Лагерра и обозначаются
называются полиномами Лагерра и обозначаются![]() :
:
1.3.Общие свойства ортогональных полиномов
Классические ортогональные* полиномы обладают целым рядом свойств, которые вытекают непосредственно из свойств ортогональности полиномов. Таким свойствами обладают любые полиномы на интервале (a,b) с произвольным весом p(x)>0.
1.Разложение произвольных полиномов по ортогональным. (Произвольный полином n-й степени qn (x) можно представить в виде линейной комбинации ортогональных полиномов pn (x))
2.Единственность системы полиномов при заданном весе.
![]() 3.Рекуррентные соотношения (для произвольных ортогональных полиномов имеет место рекуррентная формула, связывающая три последовательных полинома
3.Рекуррентные соотношения (для произвольных ортогональных полиномов имеет место рекуррентная формула, связывающая три последовательных полинома ![]()
где ![]() - некоторые постоянные
- некоторые постоянные
Глава II . Полиномы Лагерра
В математике, многочлены Лагерра, названные в честь Эдмона Лагерра (1834—1886), являются каноническими решениями Уравнения Лагерра:
![]()
являющегося линейным дифференциальным уравнением второго порядка. Многочлены Лагерра, обычно обозначающиеся как ![]() , являются последовательностью полиномов, которая может быть найдена по Формуле Родрига
, являются последовательностью полиномов, которая может быть найдена по Формуле Родрига
![]()
Эти полиномы ортогональны друг другу со скалярным произведением:
![]()
Многочлены Лагерра применяются в квантовой механике, в радиальной части решения уравнения Шредингера для атома с одним электроном. Имеются и другие применения многочленов Лагерра.
Полиномы Лагерра можно определить рекуррентной формулой:
![]()
предопределив первые два полинома как:
![]()
![]()
Обобщенные полиномы Лагерра.
![]()
где:
· ![]() **
— главное (радиальное) квантовое число;
**
— главное (радиальное) квантовое число;
· ![]() ***
— орбитальное (азимутальное) квантовое число.
***
— орбитальное (азимутальное) квантовое число.
Обобщённые полиномы Лагерра ![]() являются решениями уравнения:
являются решениями уравнения:
![]()
так что ![]() .
.
Глава III . Применение полиномов Лагерра в квантовой
механике .
Многочлены Лагерра нашли свое применение в квантовой механике:
3.1.В радиальной части решения уравнения Шредингера для атома с одним электроном (нормирование волновой функции).
Разложение ![]() волновой функции на множители, каждый из которых зависит либо от радиальной, либо от угловых координат, позволяет разбить общее условие нормировки
волновой функции на множители, каждый из которых зависит либо от радиальной, либо от угловых координат, позволяет разбить общее условие нормировки
![]()
на два: по радиальной координате
![]()
и по угловым:
![]() .
.
Для справочных целей выпишем полные выражения для нормированных волновых функций. Сумма![]() может быть выражена через так называемую гипергеометрическую функцию. Радиальная часть волновой функции с учётом условия нормировки равна
может быть выражена через так называемую гипергеометрическую функцию. Радиальная часть волновой функции с учётом условия нормировки равна
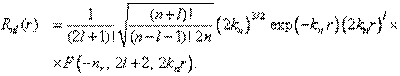
Здесь F — вырожденная (конфлюэнтная) гипергеометрическая функция (функция Куммера):
![]()
которая сходится при всех конечных z; параметр α произволен, а β предполагается не равным нулю или целому отрицательному числу. Если α есть целое отрицательное число (или нуль), то F(α, β, z) сводится к полиному степени |α|. Радиальные волновые функции выражаются также через обобщённые полиномы Лагерра ![]() :
:

3.2.Переход в осцилляторе .
Расчет переходов в осцилляторе под действием внешней силы.
Под влиянием внешней силы ![]() квантовый осциллятор может переходить с одного уровня энергии (
квантовый осциллятор может переходить с одного уровня энергии (![]() ) на другой (
) на другой (![]() ). Вероятность этого перехода
). Вероятность этого перехода ![]() для осциллятора без затухания даётся формулой:
для осциллятора без затухания даётся формулой:
![]() ,
,
где функция ![]() определяется как:
определяется как:
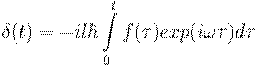 ,
,
а ![]() — полиномы Лагерра.
— полиномы Лагерра.
Заключение
В данной работе были рассмотрены полиномы - алгебраические многчлены Якоби, Эрмита и Лагерра, их форма записи, общие свойства. Более подробно рассматривались полиномы Лагерра, они нашли свое применение в квантовой механике - являются частью рассчетов вывода уравнения Шредингера и уравнения переходов в осцилляторе под действием внешней силы.
Используемая литература
1. Никифоров А. Ф., Уваров В. Б., Специальные функции математической физики, 2 изд., М., 1984
2. Суетин П. К., Классические ортогональные многочлены, 2 изд., М., 1979
3. Фок. Начало квантовой механики.
Приложение
* Если скалярное произведение двух элементов пространства равно нулю, то они называются ортогональными друг другу
** Главное (радиальное) квантовое число — целое число, обозначающее номер энергетического уровня. Характеризует энергию электронов, занимающих данный энергетический уровень. Является первым в ряду квантовых чисел, который включает в себя главное, орбитальное и магнитное квантовые числа, а также спин. Эти четыре квантовые числа определяют уникальное состояние электрона в атоме (его волновую функцию). Главное квантовое число характеризует энергию электрона. Оно обозначается как n. При увеличении главного квантового числа возрастают радиус орбиты и энергия электрона.
Наибольшее число электронов на энергетическом уровне, с учетом спина электрона определяется по формуле ![]()
*** Орбитальное квантовое число (азимутальное) - определяет азимутальное распределение плотности вероятности локализации электрона в атоме, то есть форму электронного облака и определяет энергетический подуровень данного энергетического уровня.
Связано с n -главным (радиальным) квантовым числом соотношением:
![]()
* см. приложение
** см. приложение
Похожие работы
-
Исследование трехфазного двухобмоточного трансформатора
Министерство образования Российской Федерации Пермский Государственный Технический Университет Кафедра электротехники и электромеханики Лабораторная работа № 5
-
Измерение физических величин
Цель: изучить элементарные сведения о видах измерений и оценке их точности Оборудование: штангенциркуль, микрометр, объект измерений Краткая теория:
-
Электрические цепи постоянного тока 2
Министерство образования и науки Российской Федерации Федеральное агентство по образованию Государственное образовательное учреждение высшего профессионального образования
-
Сопротивление твердых тел деформированию при динамических нагрузках
Министерство общего и профессионального образования Российской Федерации Томский Государственный Университет Физико-Технический Факультет Кафедра теории прочности и проектирования
-
Основные различия между статическим (квазистатическим) и динамическим нагружением материалов
Министерство общего и профессионального образования Российской Федерации Томский Государственный Университет Физико-Технический Факультет Кафедра теории прочности и проектирования
-
Лабораторная работа №5 Исследование электрической цепи источника постоянного тока
Министерство Российской Федерации Санкт-Петербургский государственный горный институт (технический университет) им. Г.В. Плеханова Кафедра физики
-
Изучение законов вращательного движения
Министерство общего и профессионального образования Российской Федерации Уральский Государственный Технический Университет Краснотурьинский Общетехнический Факультет
-
Определение тепловых потерь теплоизолированного трубопровода
Министерство образования Российской федерации Иркутский Государственный Технический Университет Энергетический факультет Кафедра теплоэнергетики
-
Исследование режимов работы линии электропередачи с помощью схемы замещения
Министерство образования Российской Федерации Пермский Государственный Технический Университет Кафедра электротехники и электромеханики Лабораторная работа № 1
-
Действие электрического тока на организм человека 2
Министерство образования и науки РФ Новосибирский Государственный Технический Университет Кафедра безопасности и труда Лабораторная работа №13 ДЕЙСТВИЕ ЭЛЕКТРИЧЕСКОГО ТОКА НА ОРГАНИЗМ ЧЕЛОВЕКА