Структура и свойство материалов (из конспекта лекций)

Симметрия – общее свойство материала. Характеризуется : 1) . центром симметрии ( I ), 2). плоскостью симметрии (m), 3). осью симметрии (n).

1). Это некая точка m многогранника, которая хар-ся тем, что при пересечении многогранника отсекает одинаковые части. 2). Это плоскость, которая пересекает многогранник и разделяет на 2 равные зеркальные части. 3). Это ось, которая проходит через ось (центр тяжести) при повороте кристалл совмещается сам с собой. n=360/α

(В кристаллах встречаются лишь оси симметрии 1,2,3,4 и 6 порядка. Отсутствуют 5 и 7).

Направление – [ ]; Эквивалентные направления - < >; Совокупность плоскостей - { }; Плоскость – ( ).

Гранецентрированная кубическая структура (ГЦК) – благородные (медь, серебро, золото), многовалентные (алюминий, свинец), переходные (никель, продий, палладий, иридий, платина). Каждый атом имеет 12 ближайших соседей на расстоянии а/ 2. Доля пространства заполнения шарами η=74%. Коэф. 0,74 – соответствует наиболее плотной упаковки в случае равновеликих шаров. Плотноупакованная направление в ГЦК – (101), а плотноупакованная плоскость – (111).

Гексаганально плотно упакованная структура (ГПУ) – переходные (скандий, титан, цирконий), двухвалентные (магний, цинк, кадмий). Координационное число – 12, (с/а= 8/3). Коэф. Компактности η=74%.

Объёмоцентрированная кубическая структура (ОЦК) – щелочные (литий, натрий, калий, рубидий, цезий), переходные (бром, ванадий, железо и цирконий некоторых t интервалов). Каждый атом имеет 8 ближайших соседей на расстоянии (а 2)/2. Плотноупакованная направление – (111), плотноупакованной плоскости нет. Коэф. Компактности η=68%. Это означает что, ячейка занята на 68%.

В ОЦК структуре кол-во пустот n=4. Октоэдрические пустоты – в центре куба и посередине рёбер, и окружены 6 атомами. Размер октоэдрической пустоты r₀ =0,41R. Тетраэдрические пустоты вторые по размеру, r_Т =0,225R. В ГЦК располагаются по 2 на каждой диагонали. На элементарную ячейку приходится 8 тетраэдрических пустот. ГПУ – имеет октоэдрические и тетраэдрические пустоты (r_Т =0,225R , r₀ =0,154R). ОЦК - r_Т =0,291R. В ОЦК больше пустот и большего размера, чем в ГЦК.

Закон поглощения или ослабления рентген. лучей в диф. форме : . В интегральной форме . μ – коэф. Пропорциональности ослабления либо поглощения лучей.

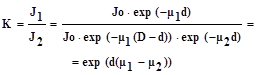
Дефекты : точечные (нульмерные) малы во всех 3 измерениях – вакансии, межузельные атомы; линейные (одномерные) малы в двух измерениях, а в третьем они большего размера (на длину зерна) – дислокации, цепочки вакансий, межузельные атомы; поверхностные (двумерные) малы только в одном измерении – границы блоков и зёрен. Точечные, линейные и поверхностные явл. микроскопическими дефектами т.е. в одном направлении измеряется атомными диаметрами. Объёмные (трёхмерные) – макроскопичны – поры и трещины. Вакансия – место с которого атом сместился из узла решетки. Если в кристалле N атомов и n вакансий то равновесная концентрация вакансий . В металлических материалах основной точечный дефект – вакансии, т.к. энергия образования междоузельного дефекта меньше энергии вакансии.

Образование точечных : дефектов: по механизму Френкеля – вакансии и межузельный атом могут одновременно образовываться при перемещении атома из его нормального положения в узле решётки (при облучении ядерными частицами); по механизму Шоттки – атом приобретает избыток Е от соседних атомов, выходит на поверхность и занимает узлы нового слоя, через время на место атома поверхностного слоя переходит атом и глубокого слоя, и вакансия перемещается в глубь кристалла.

Линейные дефекты – дислокации. Краевая дислокация – сдвиг на одно межатомное расстояние одной части кристалла относительно другой вдоль какой либо плоскости. Сдвиг создавший краевую дислокацию - ← вектор сдвига. Экстраплоскость – лишний атомный слой. В близи экстраплоскости внутри кристалла решётка сильно искажена. Если экстраплоскость находится в верхней части кристалла, то дислокация наз. положительной (┴), а если наоборот то наз. отрицательной (┬). Вектор Бёркинса (в) –явл. хар-кой дислокации по которой определяют энергию дислокации и меру искажённости кристаллической решётки дислокацией. Скольжение дислокации – перемещение дислокации по плоскости скольжения под действием касательных напряжений (в ГЦК – {111}, в ГПУ {001} ). Винтовая дислокация – атомная плоскость закрученная вокруг линии в виде геликоида. Для винтовой дислокации ось (линия) дислокации параллельна вектору Бёркинса, а направление перпендикулярно. Плотность дислокации – суммарная линия дислокаций в единице объёма

.

Поверхностные дефекты – границы зёрен и субзёрен (это поверхность по обе стороны от которой кристаллические решётки различаются пространственной ориентацией). Типы границ зёрен: граница наклона (ось вращения лежит в плоскости границы зёрен) и границы кручения (ось вращения перпендикулярна этой плоскости). Границы с разориентацией соседних зёрен менее 10° - малоугловые, а с большей разориентацией – высокоугловые. Субзёрна – разоерентированные зоны (на разные углы) зерна. Блок – часть зерна с идеальной кристаллической решёткой.