Referat.me
/ / Расчёт волновой функции в квантовой яме сложной формы

Название: Расчёт волновой функции в квантовой яме сложной формы

Вид работы: курсовая работа

Рубрика: Физика

Размер файла: 423.84 Kb

Скачать файл: referat.me-343630.pdf

Краткое описание работы: Ł Łæ æ Æ Ł — ææŁØæŒ Ø ŁŁ Œ -ˇ Æ ªæŒŁØ ª æ æ ßØ ºŁ ı Ł æŒŁØ Ł æŁ

Расчёт волновой функции в квантовой яме сложной формы

Ł Łæ æ Æ Ł — ææŁØæŒ Ø ŁŁ

Œ -ˇ Æ ªæŒŁØ ª æ æ ßØ ºŁ ı Ł æŒŁØ Ł æŁ

— æ … -ª Ł æŒ Æ

˛ º Œ ŁŒ Ł Œ ß ŁÆ ß¿

: ˚ ŁŒ ˚ æ Ł ˚ æ Ł Ł

ˆ : 3093/2 Œ º : — Ł Ł Ł æŒŁØ

ˇ º :

˚ Ł ŁØ ¨ª Ł

Œ -ˇ Æ ª

2010

˛ªº º Ł

1 ı Ł æŒ 1

2 ºŁ 1

3 — æ 4

4 ¸Ł 12


1 ı Ł æŒ

• ˝ Ø Ł ªŁŁ Ł º ß Œ ŁŁ ª Ł ª æ Ł ßı æ æ ŁØ º Œ Ł º Ø æº ø ª Ł :

, Ł

, Ł

, Ł

˙ æ .

• ˇ æ Ł ª ŁŒŁ º ßı Œ ŁØ Łı æ æ ŁØ. ´ß ŁæºŁ æ Ł Æ Ł º Œ Œ Ł æ Œ ß º Œ ßı æ æ -

ŁØ.

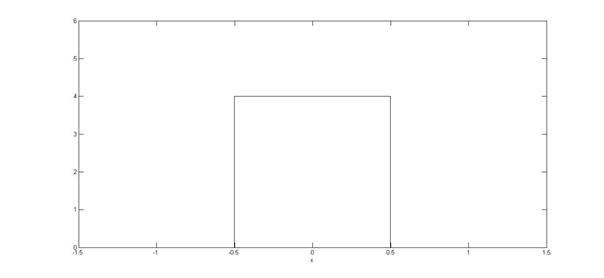
—Łæ. 1: ˇ Ł º º

2 ºŁ

˚ Œ Ł æ

Ł æº

æ ŁØ ¸ ª

Ø

ı ŁŒŁ [2],

Ł

ŁŒ º Æ Ø

ı Ł-

æŒ Ø æŁæ ß

ı Œ Ł

Œ Ł Ø ˆ Łº

. º ª

Ø

Œ ŁŁ Œ

Ø

ŁŁ æº Ł

H ˆ (ˆ Łº

Ł

) [3]. ˇ Ł

æ -

æ Ł Ł Ł

æŒ Ø æŁæ

ß Œ

Ø

ı ŁŒ Łæß

º

Œ Ł

Ψ (r,t ) [3], Œ

[4]:

æ

º

æ º ß

Ł

… Ł ª -

(1)

ˆ Łº Ł ß æ æ Ø ŒŁ Ł æŒ Ø Ł Ł º Ø

ªŁØ º Œ Ł º º [3]:

H ˆ = T ˆ + U ˆ

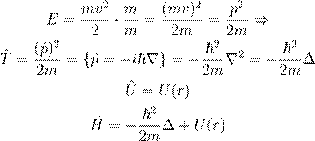
— ºŁ ß , æ º łŁæ :

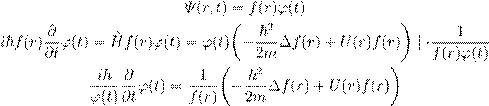(2)

ˇ æŒ º Œ

º

æ

Ł

(2)

ŁæŁ

º Œ

t ,

º Œ

r , Æ Ł º

ß

æ

Ø Ł

Ø

Œ æ

º

Ł :

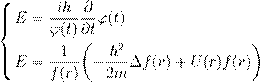
´ æ

º Ø

Æ æ

ºŁ

ı

Œ

Łæ ŁŒŁ æŁæ

ß

æ

Ł -

ßı æ æ

Ł ı,

Œ Ł

æŒŁØ Ł

æ

æ

º ºŁł

ł

Ł

-

ª

Œ ŁŁ.

Ł Ł

Ø æŁæ

ß, æ

ø ª

æ

º Ł ºŁ

ß

º

Ø

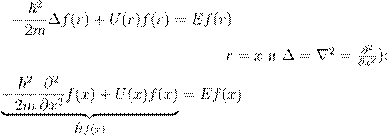… ª , Ł º º (

(3)

ŒŁ

Æ

,

ł

Ł æ

º æ Œ Ł

æ

Ø

Ł ŁŒ [1]

æ Ææ

-

ß

Ł (

æº

:

¸Ł Łºº ).

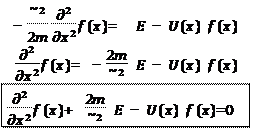(4)

´ Œ Ø ı ŁŒ º Œ Ł Ł Ł Ł æŒŁı æ Æ ŁØ -

Œº ß º Ł º ß æº Ł [4]:

• æº Ł Ł ŒŁ

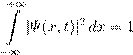(5)

˝ æ æ ß Ł ª Ł Ł ºŁ Ł Œ ŁŁ ϕ (t ):

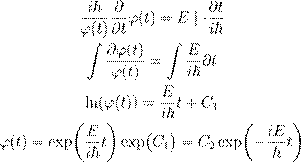
ˇ æ Ł ª Ł Ł ßÆ ŒŁ Æ , Æß Œ Ł

Ψ (x,t ) Æߺ Ł .

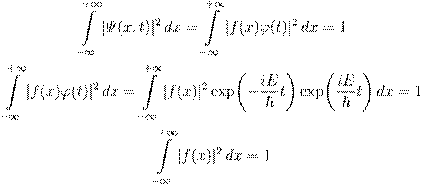(6)

•

æº Ł

ª º æ Ł

1. ´ º

Œ Ł

Ł Ł

Æ æŒ

ßı

ŁØ,

ŒŁı,

Ł ª

º (6) æ

æı

øŁ æ .

2. ´ º Œ Ł º Æß Ø Œ Ł Ø Œ Ł Ł

-

Ł, Œ Œ Œ º æ æ Ł Æ Ł æ Ł ß º

º æ .

-

3. ´ º Æ Ø Ł º Œ Ł Ł … æ ß Ł

ß

º ß Æß ß ß Ł Œ Ł Ł æ æ ßı Œ Ł

.

´ æ º Ø Ł º º (Œ ) ºŁ Ł æŒŁ æß æ Œ Ł Ø U (x ), Ł ø Ø æŁ Ł æŁ º ß −x x :

Ł-

U (−x ) = U (x )

ˇ Ł ºŁ ŁŁ Ł æŁŁ æ Ææ

ß Œ ŁŁ ˆ Łº ºŁÆ

-

Ł æŒŁ Ł

º…

… æ , ºŁÆ ª Æß Æ

ß

Œ-

ŁŁ, Ł øŁ

—

º… …

æ [3].

1. — ł Ł

Ł æ Ł æ Œ

ł Ł Ł ¸Ł

Łºº .

2. — ł Ł

º æ æ Ææ

ß Œ ŁŁ f (x ) Ł æ Ææ

ß Ł

E

( ªŁŁ)

ˆ Łº

H ˆ.

3. ˛

ß ª Ł ß æº

Ł Ł ¸Ł Łºº

º æ Ł

ß

Ł º .

4. Ææ

ß Œ ŁŁ f (x )

ƺ º… Ø … æ

ŁºŁ Ł

æ Ł

æ æ Ł .

5. — ł

º Ł Ł º , æ ł

Ł æ ł -

æ æ

æ ø æŁ

ŁŁ.

6. ˝ Œ ŁŁ f (x ) Œº ß

æ æº Ł ª º æ Ł Ł

ß æ Ł º -

Æ æ Ł æ æ Ł .

3 — æ …

• ˇ ºŁ Ł Ł Œ ŁŁ f (x ) Œ ı æŁ ª º æ Ł:

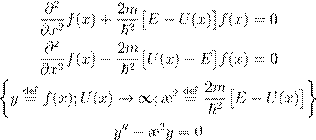
— ł Ł Ł y = ekx : k 2 ekx − æ2 2ekx = 0 ⇒ k 2 − æ2 = 0 ⇒ k = ±æ

y = C 1e æx + C 2e −æx

¨ æº Ł ª º æ Ł y : C 1 → 0 ⇒ y = C 2 e −æx

.Œ. U (x ) → ∞ ⇒ æ → ∞ ⇒ y → 0

(7)

• — ææ Ł ł Ł Ł Ł :

(8)

• — ææ Ł ł Ł Ł Ł :

y 00 − α 2 y = 0 (9)

— ł Ł Ł y = ekx : k 2 ekx − α 2 2ekx = 0 ⇒ k 2 − α 2 = 0 ⇒ k = ±α

y = C 1e αx + C 2e −αx

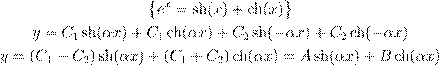
• Ł (4) º æ Œ :

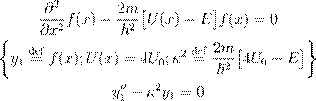
ˇ º Ł Ł (9), Æø ł Ł : y 1 = A sh(κx ) + B ch(κx )

¯æºŁ f (x ) … : (0) = 0;æºŁ f (x ) … : y 1 (0) = 0

f (x ) … :

y 1 0 = Aκ ch(κx ) + Bκ sh(κx ) y 1 0 (0) = Aκ = 0

.Œ. κ 6= 0 → A = 0

y 1 = B ch(κx ) (10)

f (x ) … :

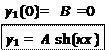(11)

• Ł (4) º æ Œ :

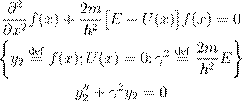
ˇ º Ł Ł (8), Æø ł Ł : y 2 = D sin(γx + ϕD ) ¨ Œ ßı æº ŁØ:

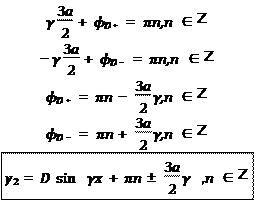(12)

•

ŒŁ

Æ

, Ψ (x )

Ł

Ł :

, Ł

y 1 + = B ch(κx ), Ł

, Ł

, Ł

, Ł

, Ł

• ¨ æº ŁØ ª º æ Ł f (x ) ß Œ æº øŁ æ ł Ł :

+ f (x ) … :

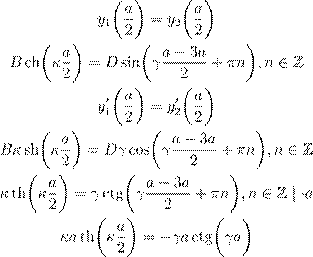
˜º Ææ ł Ł ª æ ª Ł … ß :

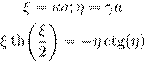(13)

− f (x ) … :

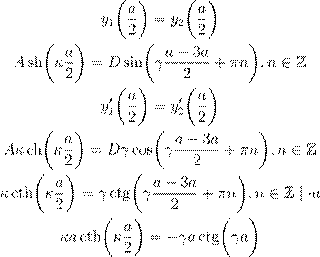
˜º Ææ ł Ł ª æ ª Ł … ß :

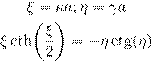(14)

• ˜º ł Ł (13) Ł (14) ææ Ł ø… Ł :

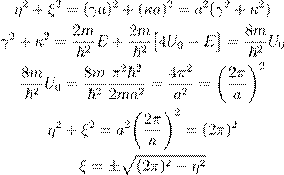(15)

• ˇ

æ

Ł

(15)

(13)Ł (14):

( … ß ł Ł )

( … ß ł Ł )

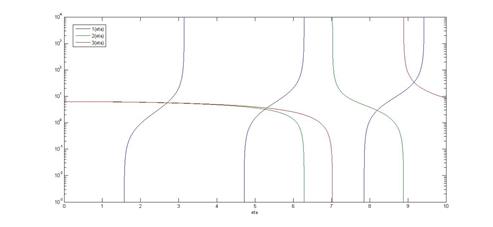
—Łæ. 2: — ł

Ł

æ

ßı

ŁØ

• — ł

ª

Ł æŒŁ æ

Ł ,

ı

Ł

æ Ææ

ß

Ł :

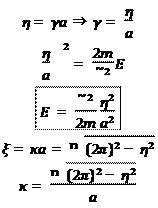(16)

• ´ … Ł Œ Ł

ŁØ f (z ):


Ł ºŁ Ł æ Ææ ßı Œ-


, Ł

y 1 + = B ch(p(2π )2 − η 2z ), Ł

, Ł

, Ł

y 1 − = A sh(p 2 − η 2 z ), Ł

(2π )

, Ł

• ¨ æº Ł Ł ŒŁ ºŁ Œ æ ß A , B Ł D , º Ææ æŁæ æ n = 0:

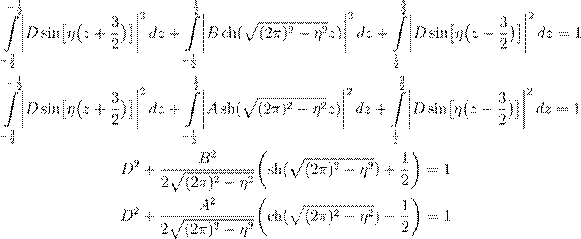
¨æ º Ł ß æ Ł, º æŁæ º … ßı ł ŁØ:

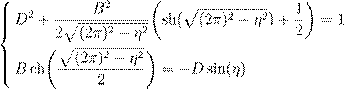
¨ º … ßı ł ŁØ:

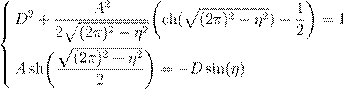
Łæº ł Ł

1. … ł Ł : η 3 = 5. 261

2. ˝ … ł Ł : η 4 = 5. 308

3. ªŁŁ ª Ł ª æ Ł ßı æ æ ŁØ º Œ Łº Ø :

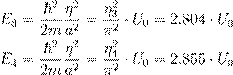
4. ´ º 3 :

ß

Œ ŁŁ:

, Ł

y 1 + = 0. 270ch(3. 435z ), Ł

, Ł

4 :

, Ł

, Ł , Ł

5. ´

æ

ı

Ł

æ Ł ß

æ Œ

ı

ß:

3 :

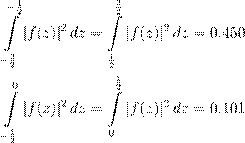
4 :

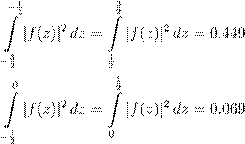
6. ˆ ŁŒŁ º ßı Œ ŁØ:

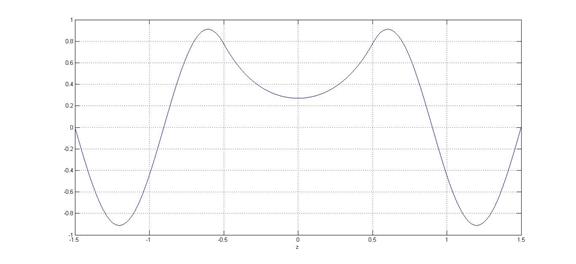
—Łæ. 3: 3 æ Ł æ æ Ł

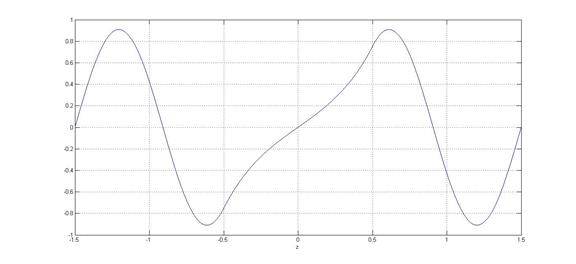
—Łæ. 4: 4 æ Ł æ æ Ł

4 ¸Ł

[1] ´. . ´º Ł Ł .

Ł

Ł æŒ Ø Ł ŁŒŁ.

.: ˝ Œ , 1988.

[2] ¸ ¸.˜., ¸Ł łŁ

Π, 1988.

¯. .

Ł æŒ Ł ŁŒ : ı

ŁŒ : 10 . .: ˝ -

[3] ¸ ¸.˜., ¸Ł łŁ

¯. .

Ł æŒ Ł ŁŒ : ˚

ı ŁŒ ( º -

Ł ŁØæŒ Ł ):

10 .

.: ˝ Œ , 1989.

[4] ˇ. . . ˜Ł Œ. ˇ Ł

Ł ß Œ

Ø ı ŁŒŁ. .: ˝

Π, 1979.

Похожие работы

  • Изучение скорости горения высокоэнергетических смесевых твердых топлив

    Определение зависимости скорости горения баллистических и смесевых порохов от давления, химической структуры взрывчатых веществ. Анализ влияния положительных и отрицательных катализаторов на горение индивидуальных взрывчатых веществ различных классов.

  • Стереометрия. Тема Движение

    Реферат по стереометрии Ученика 11 “В” класса Алексеенко Николая Тема : Движение. Спасибо за внимание ! 29.10.1995 г. Школа # 1278, кл. 11 “В”.

  • Поляризация света

    ИНСТИТУТ ФИЗИЧЕСКИХ ИССЛЕДОВАНИЙ Реферат Поляризация света. Автор: Осипян Д.С. АШТАРАК 1999 Введение Уравнения Максвелла. При наличии электрических зарядов в пространстве устанавливается возбужденное состояние, которое называют

  • Мир дискретных объектов - физика частиц. Модель частицы (корпускула). От физики Аристотеля до физики Ньютона

    Государственный комитет Российской Федерации по высшему образованию Тамбовский государственный технический университет Факультет АХП Реферат по дисциплине:

  • Двойное лучепреломление электромагнитных волн

    Управление образования. Администрация г. Екатеринбурга. Реферат по физике на тему: Двойное лучепреломление электромагнитных волн. Исполнитель 

  • Физика 10 класс Засекина профиль

    Ò.Ì. ÇÀѪʲÍÀ , Ì.Â.ÃÎËÎÂÊÎ

  • Магнитные свойства атомов

    Так как вещества взаимодействуют с внешним электромагнитным полем, то изолированные атомы обладают магнитными свойствами. Экспериментальным доказательством существования магнитного атомного момента и пространственного квантования является эффект Зеемана.

  • Разметка отверстий на развертке барабана

    Федеральное агентство по образованию РФ Белгородский государственный технологический университет имени В.Г. Шухова Кафедра: Энергетика теплотехнологии

  • Оптические волокна

    Оптическое волокно, как среда передачи данных. Конструкция оптического волокна. Параметры оптических волокон: геометрические, оптические. Оптические волокна на основе фотонных кристаллов. Передача больших потоков информации на значительные расстояния.

  • Билеты по Курсу физики для гуманитариев СПБГУАП

    1.В-во и маса, принцип эквивалентности. В-во-вид материи, кот. Обладает масой покоя. В-во слагается из элементарн. частиц.В-во всегда локализовано вограниченной части прост-ва. Его полож. можно задать с помощью огранич. числам параметров (степени свободы). Mаса хар-зует кол-во материи. Этоформулировка качественная.