Название: Рух в інерціальних системах відліку

Вид работы: учебное пособие

Рубрика: Физика

Размер файла: 89.67 Kb

Скачать файл: referat.me-343694.docx

Краткое описание работы: Неінерціальна система відліку (НІСВ). Сила інерції в неінерціальних системах відліку, що рухаються прямолінійно. Принцип еквівалентності. Рівняння відносного руху. НІСВ, що равномірно обертається навколо вісі. Коріолісова сила інерції. Теорема Коріоліса.

Рух в інерціальних системах відліку

8. РУХ В НЕ ІНЕРЦІАЛЬНИХ СИСТЕМАХ ВІДЛІКУ

1. СИЛА ІНЕРЦІЇ В НЕІНЕРЦІАЛЬНИХ СИСТЕМАХ ВІДЛІКУ, ЩО РУХАЮТЬСЯ ПРЯМОЛІНІЙНО.

Неінерціальною системою відліку (НІСВ) називають систему відліку (СВ), що рухається з прискоренням відносно інерціальної системи відліку (ІСВ).

Одержимо рівняння руху матеріальної точки відносно НІСВ. Рівняння руху – це співвідношення, якими визначаються прискорення матеріальних точок механічної системи в тій СВ, відносно якої розглядається рух.

ІСВ будемо називати нерухомою СВ, а рух відносно неї – абсолютним. Рух відносно НІСВ будемо називати відносним. НІСВ рухається відносно ІСВ з прискоренням; разом з системою рухаються і всі тіла, що в ній знаходяться; цей рух називають переносним.

Положення м.т. М в нерухомій СВ визначається радіусом-вектором (початок координат СВ – т. О); в рухомій СВ положення т. М визначається радіусом-вектором (початок координат СВ – т.). - це радіус-вектор рухомого початку відносно нерухомого О.

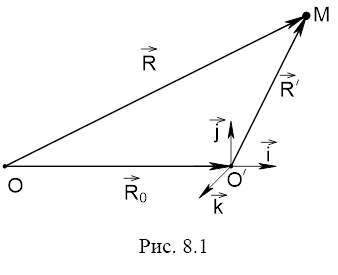
Як і раніше, час і простір вважаємо абсолютними, оскільки мова іде про повільні рухи (v<<c), тобто відстані і проміжки часу інваріантні по відношенню до переходу від однієї СВ до іншої.

Вектори в будь-який момент часу пов’язані співвідношенням:

(8.1)

Диференціюємо (8.1) двічі по t:

(8.2)

(8.3)

Обмежимося спочатку розглядом лише поступального руху системи . В цьому випадку і характеризують швидкість і прискорення не лише початку , а й будь-якої точки системи відносно О, тобто - це переносні швидкість і прискорення. при поступальному русі дають відносну швидкість і відносне прискорення. завжди дають абсолютну швидкість і абсолютне прискорення т. М:

, (8.4)

, (8.5)

причому .

В ІСВ S рівнянням руху м. т. М є рівняння 2-го закону Ньютона:

(8.6)

Підставимо (8.5) в (8.6): ; перенесемо член, що містить переносне прискорення, в праву частину:

(8.7)

Ми одержали рівняння відносного руху м.т. М. Праву частину (8.7) можна формально вважати якоюсь „силою”, що діє на м.т. Мв рухомій СВ. В цьому випадку рівняння руху м.т. в НІСВ за формою співпадає з ІІ законом Ньютона. Права частина (8.7) складається з двох складових. є рівнодійна звичайних сил (в ньютонівському розумінні сила – це результат взаємодії тіл). Друга складова – () виникає тому, що рухається з прискоренням . Її називають поступальною силою інерції:

(8.8)

Якщо не змінюється при переході від однієї СВ до іншої, то не інваріантна відносно такого переходу. Крім того, сила інерції не підлягає дії закону рівності дії і протидії. Якщо на яке-небудь тіло діє сила інерції, то не існує протидіючої сили, що прикладена до другого тіла.

Сили інерції, подібно силам тяжіння, пропорційні масі тіла. Тому в однорідному полі сил інерції, як і в полі сил тяжіння, всі тіла рухаються з одним і тим же прискоренням, незалежно від їх маси. Знаходячись в кабіні космічного корабля, який рухається поступально з прискоренням , модуль якого дорівнює g, ми виявимо, що всі тіла ведуть себе так, ніби на них діє сила . Ті ж явища ми спостерігали б, якби корабель нерухомо стояв на Землі. Не „виглядаючи” з кабіни, ми не змогли б встановити, чим зумовлена сила – прискореним рухом кабіни чи дією гравітаційного поля Землі (чи й обома причинами разом).

Ейнштейн висловив припущення, яке дістало назву принципу еквівалентності сил тяжіння і сил інерції:

Всі фізичні явища в однорідному полі тяжіння відбуваються так само, як і у відповідному однорідному полі сил інерції.

Принцип еквівалентності лежить в основі загальної теорії відносності Ейнштейна.

Отже, в СВ, що рухається поступально з прискоренням , на всі тіла діє сила інерції , що дорівнює добутку маси тіла на прискорення СВ, взяте з протилежним знаком.

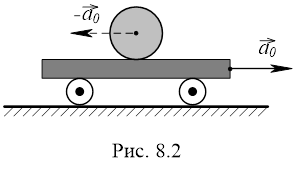
Рівняння руху м.т. в такій НІСВ має вид:

(8.9)

2. НІСВ, ЩО РІВНОМІРНО ОБЕРТАЄТЬСЯ.

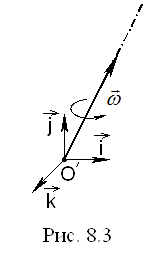
Розглянемо тепер НІСВ , яка рівномірно обертається навколо вісі, що проходить через т.О′ з кутовою швидкістю . Для спрощення вважатимемо , звідки .

Рівняння (8.2) і (8.3) матимуть вид: , .

Обчислимо похідні .

Якщо x′, y′, z′ координати т. М в , то:

(8.10)

.

Перший доданок- цевідносна швидкість м. т. М:

(8.11)

Другий доданок перетворимо, використавши відоме співвідношення, або :

, ,

Таким чином:

(8.12)

Отже:

, (8.13)

де .

Диференціюємо (8.13) по t:

; оскільки , то .

При знаходженні скористаємося тими ж міркуваннями, що і при знаходженні :

(використано вираз (8.12)).

Нарешті:

(8.14)

В (14) останній доданок

(8.15)

є переносним прискоренням; таке прискорення зазнає нерухома точка в CВ, що обертається.

Доданок (8.16)

залежить як від відносного так і від переносного руху точки.

Це прискорення дістало назву коріолісового прискорення.

Отже:

(8.17)

Абсолютне прискорення є векторною сумою відносного, коріолісового та переносного прискорень.

Це твердження називають теоремою Коріоліса.

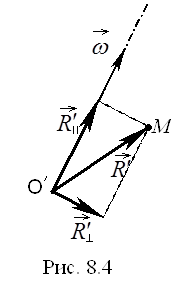Обчислимо переносне прискорення. Розкладемо вектор на дві складові: і - перпендикулярну і паралельну вісі обертання.

тому

За властивістю подвійного векторного добутку:

, (8.18)

оскільки

Очевидно в даному випадку (і ) є доцентровим прискоренням.

Підставимо тепер в (8.6) (8.17) і врахуємо (8.16) і (8.18):

;

;

(8.19)

До „справжніх” сил додалися дві сили інерції:

коріолісова сила : (8.20)

і відцентрова сила : (8.21)

Коріолісова сила інерції виникає тільки тоді, коли CВ обертається, а м.т. М рухається відносно цієї системи. При і .

,тому під час відносного руху вона роботи не виконує; змінює тільки за напрямком .

Якщо система відліку , крім обертового руху, здійснює ще й поступальний, тоі В цьому випадку переносна швидкість і переносне прискорення визначаться співвідношеннями :

,

а рівняння відносного руху м.т. в НІСВ має вид:

(8.22)