Название: Метод аппаратурной имитации случайных чисел, относящихся к нечётким множествам
Вид работы: доклад
Рубрика: Информатика и программирование
Размер файла: 42.98 Kb
Скачать файл: referat.me-133858.docx
Краткое описание работы: Одним из важных этапов разработки различных образцов техники, систем управления и регулирования является изучение их функционирования в условиях случайных факторов.
Метод аппаратурной имитации случайных чисел, относящихся к нечётким множествам
А.Ф. Гришков, А.А. Маргелов, А.В. Маргелов
Одним из важных этапов разработки различных образцов техники, систем управления и регулирования является изучение их функционирования в условиях случайных факторов.
Особый класс в технике имитации случайных факторов образуют генераторы случайных чисел, относящихся к нечётким множествам (ГСЧ НМ) [1,2]. Однако, известные генераторы [2,3,4] сложны и имеют низкую надёжность.
Предлагается структура ГСЧ НМ, реализующая метод формирования нечётких чисел, соответствующий способу настройки аппаратуры на значение параметров, заданных нечётко. На рис.1 представлена диаграмма, поясняющая принцип реализации указанного метода и работу предлагаемого генератора.
Пусть из некоторой точки Х=0 параметр Х увеличивается дискретно с шагом, имеющим постоянную ![]() Х и случайную
Х и случайную ![]() составляющие, где i - номер шага. Считаем, что нечёткая цель достигается, если текущее значение Х попадает в интервал [
составляющие, где i - номер шага. Считаем, что нечёткая цель достигается, если текущее значение Х попадает в интервал [![]() ,
, ![]() ]. Это будет осуществляться по следующим правилам.
]. Это будет осуществляться по следующим правилам.
Одновременно с очередным шагом следования к интервалу разыгрывается случайный уровень ![]() - функция принадлежности типа примерного равенства, определяемая уравнением:
- функция принадлежности типа примерного равенства, определяемая уравнением:
при а-![]()
при а<x![]() (1)
(1)
при a+![]() <x<a-
<x<a-![]()
М(Х) = 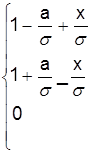
где а и ![]() - соответственно среднее значение и полуразмах носителя функции принадлежности.
- соответственно среднее значение и полуразмах носителя функции принадлежности.
Для каждого текущего значения Х в соответствии с уравнением (1) определяем значение М(Х) функции принадлежности и сравниваем со случайным уровнем ![]() .
.
При выполнении условия М(Х)![]() (2) принимаем решение, что текущее значение Х попало в интервал [
(2) принимаем решение, что текущее значение Х попало в интервал [![]() ,
, ![]() ].
].
На рис.2 представлена структурная схема генератора случайных чисел, реализующая предлагаемый метод, которая содержит генератор одиночного импульса 1, счётчик импульсов 2, элементы памяти 3,4 и 5, генератор тактовых импульсов 6, датчик равномерно распределённых чисел 7, сумматор 8, регистр памяти 9, накапливающий сумматор 10, постоянное запоминающее устройство 11, элементы сравнения 12 и 13.
Генератор работает следующим образом. Генератор 1 формирует одиночный импульс, под действием которого счётчик 2 и сумматор 10 обнуляются, а генератор 6 запускается. Счётчик 2 начинает подсчитывать тактовые импульсы генератора 6. Кроме того, с каждым тактовым импульсом на выходе датчика 7 формируются числа ![]() , равномерно распределённые в интервале [0,1], которые поступают непосредственно на вход сумматора 8 и через элемент 4, время задержки которого равно одному периоду следования импульсов генератора 6, на вход элемента сравнения 12.
, равномерно распределённые в интервале [0,1], которые поступают непосредственно на вход сумматора 8 и через элемент 4, время задержки которого равно одному периоду следования импульсов генератора 6, на вход элемента сравнения 12.
Число ![]() с выхода датчика 7 суммируется в сумматоре 8 с постоянной величиной
с выхода датчика 7 суммируется в сумматоре 8 с постоянной величиной ![]() Х, а результат их суммы по тактовому импульсу (при необходимости с задержкой) заносится в сумматор 10.
Х, а результат их суммы по тактовому импульсу (при необходимости с задержкой) заносится в сумматор 10.
Поскольку сигнал на выходе “меньше или равно” элемента 13 и входе задания знака суммирования сумматора 10 соответствует логической “1”, сумматор 10 работает в режиме суммирования. Описанные процессы повторяются, и число на выходе сумматора 10 увеличивается, оставаясь случайным.
Код числа Х с выхода сумматора является адресным кодом для постоянного запоминающего устройства 11, на выходе которого формируется значение М(Х) функции принадлежности в соответствии с уравнением (1).
Значение этой функции поступает непосредственно на входы элементов 12 и 13, через элемент 5, время задержки которого равно одному периоду следования импульсов генератора 6, на другой вход элемента 13. На другом входе элемента 12 формируется случайный уровень ![]() . Поскольку числа на выходе датчика некоррелированы, этот уровень формируется с помощью элемента 4 путём задержки числа
. Поскольку числа на выходе датчика некоррелированы, этот уровень формируется с помощью элемента 4 путём задержки числа ![]() с выхода датчика 7 на один период следования импульсов генератора 6, т.е.
с выхода датчика 7 на один период следования импульсов генератора 6, т.е. ![]() . Элемент 12 осуществляет проверку выполнения условия (2) и если это условие не выполняется, то сигнал на выходе “меньше или равно” этого элемента соответствует логическому “0” и генератор 6 продолжает формировать тактовые импульсы. Если же это условие выполняется, что означает попадание числа Х в интервал [
. Элемент 12 осуществляет проверку выполнения условия (2) и если это условие не выполняется, то сигнал на выходе “меньше или равно” этого элемента соответствует логическому “0” и генератор 6 продолжает формировать тактовые импульсы. Если же это условие выполняется, что означает попадание числа Х в интервал [![]() ,
, ![]() ], то сигнал на выходе элемента 12 изменяется на логически инверсный “1” и генератор 6 прекращает формировать тактовые импульсы.
], то сигнал на выходе элемента 12 изменяется на логически инверсный “1” и генератор 6 прекращает формировать тактовые импульсы.
В результате на выходах генератора формируются два числа (на выходе счётчика 2 и выходе сумматора 10). Первое из них соответствует нечёткому значению интервала времени, необходимого для достижения поставленной цели, а второе - нечёткому значению результата настройки.
В отличие от известных предложенный метод (алгоритм) позволил создать простой по своей структуре генератор случайных чисел, у которого наработка на отказ в 1.5 раза больше, чем у аналогичных.
Список литературы
В.Н. Четвериков, Э.А. Баканович. Стахостические вычислительные устройства систем моделирования. М.: Машиностроение, 1989.
Вероятностные автоматы и их приложения. Сб.ст. под ред. Р.Г. Бухарива Изд-во Казанского университета, 1986.
Э.В. Борисов, С.Н. Воробьёв, Е.С. Егоров. Генератор случайных чисел. Авт. свид. 1605230, кл. GOGG 7/58, бюл. №41, 1990.
Г. Хан, С. Шапиро. Статистические модели в инженерных задачах. М.: Мир, 1967.
Похожие работы
-
Лабораторная работа по информатике ( практика )
Лабораторная работа 4 ИЗУЧЕНИЕ ПРИНЦИПОВ ОРГАНИЗАЦИИ АРИФМЕТИКО-ЛОГИЧЕСКИХ УСТРОЙСТВ. СТРУКТУРА АЛУ ДЛЯ ДЕЛЕНИЯ ЧИСЕЛ С ФИКСИРО- ВАННОЙ ЗАПЯТОЙ Ц е л ь р а б о т ы: Изучение принципов построения и функционирования АЛУ для деления чисел с фиксированной запятой.
-
Изучение принципов организации арифметико-логическиз устройств. Структура алу для умнлжения чисел с фиксированной запятой
Ц е л ь р а б о т ы: Изучение принципов построения и функционирования АЛУ для умножения чисел с фиксированной запятой. В в е д е н и е В ЭВМ операция умножения чисел с фиксированной запятой с
-
Лаба по информатике
Министерство общего и профессионального образования РФ Владимирский Государственный Университет Кафедра УИТЭС Лабораторная работа N2 ИЗУЧЕНИЕ ПРИНЦИПОВ ОРГАНИЗАЦИИ АРИФМЕТИКО-
-
Старый взгляд на новые вещи
Оглянитесь вокруг и вы поймёте, что миром правят случайности - они везде и всюду: от шума в радиоприёмнике, до игры в орлянку и карт Таро, от русской рулетки и до ... генерирования паролей. И ведь не известно, что более опасно.
-
Создание компьютерной графики при помощи OpenGL
Написание программы вывода графика функции с помощью точек и линий, модификация программы. Программа вывода каркаса вращающегося тора относительно своей оси с одновременным движением по заданной траектории. Создание эффекта сползания текстуры с цилиндра.
-
Моделирование датчиков случайных чисел с заданным законом распределения
Проектирование датчика случайных чисел, пригодного для моделирования случайной последовательности с заданным законом распределения. Методы моделирования. Разработка алгоритма и программы датчика. Исследование свойств выработанной им последовательности.
-
Проверка гипотезы о нормальности закона распределения экспериментальных данных
Моделирование работы генератора случайных двоичных чисел с ограниченной последовательностью 0 и 1, подчиняющегося равномерному закону распределения, заданному с помощью модели Гильберта. Представление программного решения задачи средствами языка С++.
-
Применение датчиков случайных чисел для имитации реальных условий
Применение случайных чисел в моделировании, выборке, численном анализе, программировании и принятии решений. Понятие равномерного распределения вероятности. Способы получения последовательности. Правила выбора модуля. Критерий Колмогорова-Смирнова.
-
Перестановка строк и столбцов массива случайным образом
Вектор и матрица с числовыми компонентами как математические прообразы массивов. Создание программы, содержащей процедуры для выполнения заданных операций: построение массива, перестановка строк и столбцов. Использование диалоговых окон "уведомлений".
-
Разработка виртуального вычислительного устройства с многослойной структурой
Разработка виртуального вычислительного устройства с кассетной структурой. Массивы и кластеры. Вычисления над элементами массива. Вычислительные функции пакета LabVIEW. Логическая последовательность выполнения отдельных частей программы (подпрограммы).