Название: Вычисление интеграла

Вид работы: реферат

Рубрика: Информатика и программирование

Размер файла: 32.4 Kb

Скачать файл: referat.me-135415.docx

Краткое описание работы: Вычисление определённого интеграла с помощью метода трапеций на компьютере.

Вычисление интеграла

МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ СТРОИТЕЛЬНЫЙ УНИВЕРСИТЕТ

КУРСОВАЯ РАБОТА

тема:

«Вычисление определённого интеграла

с помощью метода трапеций

на компьютере»

Выполнил:

студент ф-та

ЭОУС-1-12

Зыков И.

Принял:

Зоткин С. П.

Москва 2001

1. Введение:

Определенный интеграл от функции, имеющей неэлементарную первообразную, можно вычислить с помощью той или иной приближенной формулы. Для решения этой задачи на компьютере, можно воспользоваться формулами прямоугольников, трапеций или формулой Симпсона. В данной работе рассматривается формула трапеций.

Пусть I = ò f ( x ) dx , где f ( x ) – непрерывная функция, которую мы для наглядности будем предполагать положительной. Тогда I представит собой площадь криволинейной трапеции, ограниченной линиями x = a , x = b , y =0, y = f ( x ) . Выберем какое-нибудь натуральное число n и разложим отрезок[ a , b ] на n равных отрезков при помощи точек x 0 = a < x 1 <…< x n = b . Прямые x = x iразбивают интересующую нас криволинейную трапецию на n полосок. Примем каждую из этих полосок за обыкновенную прямолинейную трапецию (рис. 1, где n =4).

рис. 1

Тогда площадь первой слева полоски будет приближенно выражаться числом

((f(x 0 )+f(x 1 ))/2) *(x 1 -x 0 )=((y 0 +y 1 )/2) *((b-a)/n) ,

ибо основания трапеции, за которую мы принимаем полоску, равны f ( x 0 )= y 0 и f ( x 1 )= y 1 , а высота её

x 1 -x 0 =(b-a)/n .

Аналогично площади дальнейших полосок выразятся числами

(y 1 +y 2 ) *((b-a)/2 *n) , (y 2 +y 3 ) *((b-a)/2 *n) , … , (y n-1 +y n) *((b-a)/2 *n) .

Значит, для нашего интеграла получается формула

I » ((b-a)/2 *n) *[ y 0 +2 *(y 1 +…+y n-1)+y n] .

Пологая для краткости y 0 + y n= Y кр (крайние), y 1 + y 2+…+ y n-1 = Y пром (промежуточные), получим

ò ydx » ((b-a)/2 * n) *(Y кр+2 *Y пром)

Эту формулу можно записать в другом виде

ò f(x)dx » (h/2) *[ f(a)+f(b)+2 å f(x i) ]

(где h – длина одного из n равных отрезков, x i = a + i * h ). Эта приближенная формула и называется формулой трапеций. Она оказывается тем более точной, чем больше взятое нами число n . Погрешность одного шага вычисляется по формуле: -( h ^3)/12 .

Задача. Пусть нужно проинтегрировать функцию f ( x ) = x ³ +2x²-3 x -8 на отрезке [0, 6]. На этом отрезке функция непрерывна.

Для выполнения поставленной задачи составлена нижеописанная программа, приближенно вычисляющая определенный интеграл с помощью метода трапеций. Программа состоит из трех функций main , f и trap . Функция main позволяет ввести интервалы интегрирования и задать точность вычисления интеграла, а также вызывает функцию trap для вычисления интеграла и распечатывает на экране результат. Функция f принимает аргумент x типа float и возвращает значение интегрируемой функции в этой точке. Trap – основная функция программы: она выполняет все вычисления, связанные с нахождением определенного интеграла. Trap принимает четыре параметра: пределы интегрирования типа float (a и b ), допустимую относительную ошибку типа float и указатель на интегрируемую функцию. Вычисления выполняются до тех пор, пока относительная ошибка, вычисляемая по формуле | S-Sn |, не будет меньше или равна требуемой. Функция реализована с экономией вычислений, т. е. учитывается, что S 0 постоянная и S 1= S 1+ f ( a +(2 *i +1) *h ) , поэтому эти значения вычисляются единожды. Метод трапеций обладает высокой скоростью вычисления, но меньшей точностью, чем метод Симпсона, поэтому его применение удобно там, где не требуется очень высокая точность.

Ниже предлагается блок-схема, листинг, спецификации, ручной счет и результат работы программы на примере поставленной выше задачи. Блок-схема позволяет отследить и понять особенности алгоритма программы, спецификации дают представление о назначении каждой переменной в основной функции trap , листинг - исходный код работающей программы с комментариями, а ручной счет предоставляет возможность проанализировать результаты выполнения программы.

2. Блок-схема программы:

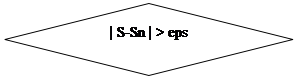
ДА

НЕТ

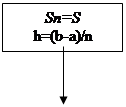i=1

S1=S1+f(a+(2*i+1)*h)

i=n/2

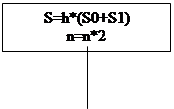3. Листинг:

# include<stdio.h>

#include<math.h>

#include<conio.h>

main()

{

double a,b,er,eps,f(double),s,trap(double,double,double,double(*)(double));

clrscr();

printf("n Задайте пределы интегрирования и точность: ");

scanf ("%lf%lf%lf",&a,&b,&eps);

s=trap(a,b,eps,f);

printf("n Интеграл от a=%3.2lf до b=%3.2lf равен %lf",a,b,s);

getch();

}

double f(double x)

{

return x*x*x+2*(x*x)-3*x-8;

}

double trap(double a,double b,double eps,double(*f)(double))

{

double h,s,s0,s1,sn;

int i,n;

s=1; sn=101;

n=4;

s0=(f(a)+f(b))/2;

s1=f((a+b)/2);

while(fabs(s-sn)>eps){

sn=s;

h=(b-a)/n;

for(i=0; i<n/2; i++)

s1+=f(a+(2*i+1)*h);

s=h*(s0+s1);

n*=2;

}

return s;

}

4. Спецификации:

Имя переменной	Тип	Назначение
n	int	число разбиений отрезка [a, b]
i	int	счетчик циклов
a	double	Нижний предел интегрирования
b	double	Верхний предел интегрирования
h	double	шаг разбиения отрезка
eps	double	допустимая относительная ошибка
f	double(*)	указатель на интегрируемую фун - цию
x	double	аргумент ф-ии f
s	double	текущий результат интегрирования
s0	double	половина суммы значений функции в точках a и b
s1	double	сумма значений функции в промежуточных точках
sn	double	предыдущий результат интегрирования

5. Ручной счет:

Xi	Yi
0	-8
0,75	-8,703125
1,5	-4,625
2,25	6,765625
3	28
3,75	61,609375
4,5	110,125
5,25	176,078125
6	262

6. Результат работы программы:

при eps = 0.1 при eps = 0.001

Введите a, b, eps: Введите a, b, eps:

0 0

6 6

.1 .001

Интеграл= 366.024170 Интеграл= 366.000094

т.е с помощью этой программы можно вычислить интеграл от функции с точностью до 1/10000.