Название: Поиск кратчайшего пути в многоугольнике

Вид работы: курсовая работа

Рубрика: Информатика и программирование

Размер файла: 159.56 Kb

Скачать файл: referat.me-135871.docx

Краткое описание работы: Разработка программы в среде Delphi для нахождения кратчайшего пути между стартом, лежащим в одной из вершин многоугольника, и финишем, находящимся на одной из сторон. Установка опорных точек, контроль целостности вводимых данных, методы решения задачи.

Поиск кратчайшего пути в многоугольнике

Агентство по образованию

Тихоокеанский государственный экономический университет

Экономический институт

Поиск кратчайшего пути в многоугольнике

Выполнил: Матвеев А.В.

Владивосток 2009

Введение

Условие решаемой задачи дословно по заданию звучит следующим образом: «В заданном m-угольнике найти кратчайший путь между стартом, лежащим в одной из его вершин, и финишем, находящимся на одной из его сторон».

Для большей эффективности положим старт и финиш произвольными точками внутри m-угольника, выбираемыми пользователем. Предоставим возможность выбирать размерность поля N на N для дальнейшего построения внутри неё, создаваемого пользователем, m-угольника. Графически покажем один из кратчайших путей между стартом финишем.

Перед началом вычисления пользователь должен указывать в программе следующую информацию

- размер поля;

- кол-во опорных точек, для построения m-угольника

- местоположение вершин m-угольника(с помощью мыши)

-место положение финиша и старта внутри m-угольника(также с помощью мыши)

После установки опорных точек программа должна определять принадлежность той или иной точки к внутренней области m-угольника, после чего просчитывать кратчайший путь с учётом доступности(внутри m-угольника) и не доступности(вне m-угольника) точек и, в соответствии с этим, отбирать те из них, которые задействованные в пути.

Программа должна отображать поле, область(m-угольник) и путь между стартом и финишем.

Необходимо предусмотреть контроль целостности вводимых данных, таких как размер поля и кол-во опорных точек.

Не допустить совпадения финиша и старта или установку их вне области а так же дать возможность в заранее построенной области изменять их положение.

Формальная постановка задачи

Положим поле двумерным массивом Shape’ов, основные функции которого дать пользователю возможность задания вершин m-угольника, старта и финиша, а также графическое отображение работы программы. В соответствии ему поставим двумерный булевый массив(доступные и недоступные точки).

Используя булевую матрицу и координаты старта и финиша вычисляем точки кратчайшего пути, которые далее отображаем с помощью массива Shape’ов.

Методы решения задачи

Локализация точек

Существует довольно много различных методов решения подобной задачи, каждый из которых основывается на своих принципах и приемах, имеет уникальные преимущества и, соответственно, недостатки. В данной работе был использован наиболее простой и менее громоздкий с учётом того, что на поле между точками имеется некоторое расстояние.

Суть используемого метода в следующем. По заданным вершинам строится полигон и заливается цветом, отличным от цвета фона. Далее для каждой точки идёт проверка цвета канвы. Если цвет канвы в данной точке совпадает со цветом заливки полигона то точка принадлежит заданной области.

Построениеполигона:

with canvas do begin

setlength(tochka,m);

for i:=0 to m-1 do begin

tochka[i].X:=integer(vershina[i].x^)+round(h/(4*n));

tochka[i].Y:=integer(vershina[i].y^)+round(h/(4*n));

end;

Pen.Color:=clred;

Polygon(tochka);

brush.color:=clred;

end;

end;

Здесьздесь vershina[].хи vershina[].ууказателина Top и Left Shape’ов, tochka[]-массивкоординатцентровэтих Left Shape’ов.

Проверкацвета:

for i:=0 to n-1 do

for j:= 0 to n-1 do

if canvas.Pixels[a[i,j].Left+round(h/(4*n)),a[i,j].Top+round(h/(4*n))]=clred then

a[i,j].Brush.Color:=clgreen;

Также приведём пример решения этой задачи в более общем случае. Его суть в том, что вначале строится контур области, а потом для каждой точки идет подсчёт кол-ва пересечений горизонтали, проведённой через эту точку, с контурами области слева от определяемой точки. Если кол-во нечётно то она принадлежит области, иначе не принадлежит.

Приведём текст такого метода:

dx:=(bx-ax)/m;

расстояние по горизонтали между двумя соседними точками ребра

dy:=(by-ay)/m;//по вертикали

{Локализация}

x:=ax+dx/2;

for i:=1 to m do begin

y:=ay+dy/2;

//WriteLn(fout);

for j:=1 to m do begin

//Write(fout,'(',x:0:1,',',y:0:1,')',' ');

{(x,y)-локализация}

L:=0; {Число пересечений слева}

for k:=1 to n-1 do begin

x1:=xv[k]; y1:=yv[k]; {Ребро}

x2:=xv[k+1]; y2:=yv[k+1];

if ((y1<y2) and (y1<y) and (y<y2)) or

((y2<y1) and (y2<y) and (y<y1)) then begin

{Уравнение прямой через 2 точки}

x3:=(y-y1)/(y2-y1)*(x2-x1)+x1;

if x3<x then L:=L+1;

end;

end;

y:=y+dy;

//WriteLn(fout,'L=',L);

if (L mod 2) =0 then b[m-j+1,i]:=0 else b[m-j+1,i]:=1;

end;

x:=x+dx;

end;

for i:=1 to m do begin

WriteLn(fout);

for j:=1 to m do begin

Write(fout,b[i,j]);

end;

end;

Поиск кратчайшего пути

Суть реализованного алгоритма состоит в том что, в соответствие булевой матрице, отражающей доступность точек, ставится целочисленная матрица меток. В её элементы записываются кол-ва ходов, за которое можно попасть из финиша в данную точку булевой матрицы. Когда устанавливается значение в метку, соответствующий старту начинается обратный ход. Программа ищет соседнюю старту точку, метка которой на 1 меньше метки старта. Далее из найденной точки повторяется та же операция и так до тех пор пока не будет достигнут финиш.

procedure Tgraph.find(var z:Tmatrix;a,b:Txy;n:Integer);

var i,j,i1,j1:integer;

c:Integer;//для записи значений в метки

yyy:Boolean;//используется как условие выхода из цикла

LABEL LBL;

begin

ny:=0;//длина пути

//зополнение матрицы меток бесконечностями

for i:=0 to n-1 do

for j:=0 to n-1 do metka1[i,j]:=$7fff;

metka1[b.x,b.y]:=0;//метка соответствующая финишу

//процедура записывает в конкретную метку кол-во ходов,

//необходимых чтобы попасть в неё с финиша

c:=-1;

while 1000>=c do begin

c:=c+1;

for i:=0 to n-1 do begin

for j:=0 to n-1 do begin

if metka1[i,j]=c then begin

for i1:=-1 to 1 do begin

for j1:=-1 to 1 do begin

if (i1=0) and (j1=0) then continue;//что бы не проверять саму точку

if not z[i+i1,j+j1] or (metka1[i+i1,j+j1]<>$7fff) then continue;//точка не доступ- //на или путь к ней отсутствует

metka1[i+i1,j+j1]:=c+1;

if (i+i1=a.x) and (j+j1=a.y) then begin//попалинастарт

goto LBL;

end;

end;

end;

end;

end;

end;

end;

//запись полученной матрицы меток в текстовый файл

LBL:

//процедура двигаясь от старта к финишу по полученным меткам

//заносит пройденные точки в массив точек пути

if metka1[a.x,a.y]=$7fff then begin

exit;

end;

c:=metka1[a.x,a.y];//кол-во ходов от старта до финиша

i:=a.x;

j:=a.y;

yWay[1]:=a;

ny:=1;//кол-во точек, использованных в пути

while c>0 do begin

c:=c-1;

yyy:=False;

for i1:=-1 to 1 do begin

for j1:=-1 to 1 do begin

if (i1=0) and (j1=0) then continue;//чтобынепроверятьсамуточку

if metka1[i+i1,j+j1]<>c then continue;

ny:=ny+1;//увеличение длины пути

yWay[ny].x:=i+i1;//добавление точки

yWay[ny].y:=j+j1;// в путь

if (i+i1=b.x) and (j+j1=b.y) then exit;

i:=i+i1;

j:=j+j1;

yyy:=TRUE;//используется для выхода из первого цикла “FOR”

break;

end;

if yyy then break;

end;

end;

end;

Текст программы

В данном пункте приводятся тексты основного модуля без текста модуля для расчёта пути, так как его главная часть приведена выше.

unit MainUnit;

interface

uses

Windows, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms,

Dialogs, ExtCtrls, StdCtrls,Sgraph;

Const

nMaxShape=25;

type

coordinate=record

x:pointer;

y:pointer

end;

razmetka=array[0..nMaxShape,0..nMaxShape] of TShape;

TForm1 = class(TForm)

Panel1: TPanel;

btnstroi: TButton;

btnfinish: TButton;

btnstart: TButton;

btnnew: TButton;

Edit1: TEdit;

Edit2: TEdit;

btnGraph: TButton;

Label1: TLabel;

Label2: TLabel;

procedure matriza();

procedure btnstroiClick(Sender: TObject);

procedure btnnewClick(Sender: TObject);

procedure vershini(Sender: TObject; Button: TMouseButton;

Shift: TShiftState; X, Y: Integer);

procedure FormCreate(Sender: TObject);

procedure btnstartClick(Sender: TObject);

procedure btnfinishClick(Sender: TObject);

procedure FormPaint(Sender: TObject);

procedure FormResize(Sender: TObject);

procedure btnGraphClick(Sender: TObject);

private

{ Private declarations }

public

{ Public declarations }

function min(x,y:integer):integer;

procedure DrawWay;

procedure myShape;

public

k:integer;

a:razmetka;

end;

var

index1,index2:boolean;//проверкавозможностирасчёта

Form1: TForm1;

n,h,m:integer;

vershina: array of coordinate;

tochka:array of Tpoint;

matr: TMatrix;

nachialo,konez:Txy;

implementation

{$R *.dfm}

//выбор и отображение нужного кол-ва Shape'ов

procedure TForm1.myShape;

var i,j:integer;

begin

for i:=0 to n-1 do

for j:=0 to n-1 do begin

a[i,j].Shape:=stcircle;

a[i,j].Parent:=self;

a[i,j].Brush.Color:=clwhite;

a[i,j].Height:=round(h/(2*n));

a[i,j].Width:=round(h/(2*n));

a[i,j].Top:=round(i*h/n);

a[i,j].Left:=round(j*h/n);

a[i,j].Show;

end;

end;

//созданиемассивашейпов

procedure TForm1.btnstroiClick(Sender: TObject);

var i,j:integer;

begin

try

m:=strtoint(edit2.Text);//кол-во опорных точек

n:=strtoint(edit1.Text);//размерность

if (n<=nMaxShape)and(m<n)then begin

setlength(vershina,m); myShape();btnStroi.Enabled:=False

end

else begin

application.MessageBox ('введитекол-воточек<размерность<'+'25','ошибка');

edit1.Clear;edit2.clear; edit1.SetFocus;

end;

except

application.MessageBox('введитецелоечисло','ошибка');

edit1.Clear;edit1.Clear;edit1.SetFocus;

end;

end;

procedure TForm1.btnnewClick(Sender: TObject);

var j,i:integer;

begin

wGraph.ny:=0; //Нетпути

k:=0;

for i:=0 to n-1 do

for j:=0 to n-1 do a[i,j].Hide;

invalidate;

edit1.Clear;

edit1.SetFocus;

edit2.Clear;

index1:=false;index2:=false;

btnStroi.Enabled:=True;

end;

//создание области по выбранным вершинам(ShapeClick)

procedure TForm1.vershini(Sender: TObject; Button: TMouseButton;

Shift: TShiftState; X, Y: Integer);

var i,j:integer;

begin

if k<m then

begin //получение массива точек для полигона

vershina[k].x:=@(sender as TShape).left;

vershina[k].y:=@(sender as TShape).top;

(sender as TShape).brush.Color:=clgreen;

k:=k+1;

if k=m then

begin formpaint(self);//закраскаобласти

//определение принадлежности точки области

for i:=0 to n-1 do

for j:= 0 to n-1 do

if canvas.Pixels[a[i,j].Left+round(h/(4*n)),a[i,j].Top+round(h/(4*n))]=clred then

a[i,j].Brush.Color:=clgreen;

btnstart.Enabled:=true;

btnfinish.Enabled:=true;

invalidate

end;

end;

//изменениеначала

if ((btnstart.Tag=1)and((sender as tshape).Brush.Color=clyellow))

then index2:=false;

if (btnstart.Tag=1)and((sender as tshape).Brush.Color=clgreen)

or((btnstart.Tag=1)and((sender as tshape).Brush.Color=clyellow))

then begin(sender as tshape).Brush.Color:=clblue;index1:=true;

btnstart.Tag:=0 end;

//изменениеконца

if ((btnfinish.Tag=1)and((sender as tshape).Brush.Color=clblue))

then index1:=false;

if (btnfinish.Tag=1)and((sender as tshape).Brush.Color=clgreen)

or((btnfinish.Tag=1)and((sender as tshape).Brush.Color=clblue))

then begin btnfinish.Tag:=0;index2:=true;

(sender as tshape).Brush.Color:=clyellow end;

if (index1=true) and (index2=true) then btnGraph.Enabled:=true;

end;

procedure TForm1.FormCreate(Sender: TObject);

var i,j,n:integer;

begin

k:=0;

panel1.Tag:=0;

btnstart.Enabled:=false;

btnfinish.Enabled:=false;

btnGraph.Enabled:=false;

n:=nMaxShape;

//self.WindowState:=wsMaximized;

for i:=0 to n-1 do

for j:=0 to n-1 do begin

a[i,j]:=tshape.Create(self);

a[i,j].Shape:=stcircle;

a[i,j].Parent:=self;

a[i,j].Brush.Color:=clwhite;

a[i,j].Height:=41;

a[i,j].Width:=41;

a[i,j].Top:=round(i*100/n);

a[i,j].Left:=round(j*100/n);

a[i,j].onmousedown:=form1.vershini;

WriteLn(wgraph.fout,i:3,j:3);

a[i,j].Hide;

end;

end;

//постановканачала

procedure TForm1.btnstartClick(Sender: TObject);

var i,j:integer;

begin

index1:=false;

btnstart.Tag:=1;

for i:=0 to n-1 do

for j:= 0 to n-1 do

if a[i,j].Brush.Color=clblue then

a[i,j].Brush.Color:=clgreen

end;

//постановкаконца

procedure TForm1.btnfinishClick(Sender: TObject);

var i,j:integer;

begin

index2:=false;

btnfinish.Tag:=1;

for i:=0 to n-1 do

for j:= 0 to n-1 do

if a[i,j].Brush.Color=clyellow then

a[i,j].Brush.Color:=clgreen

end;

procedure TForm1.FormPaint(Sender: TObject);

var i:integer;

begin

if k=m then begin

with canvas do begin

setlength(tochka,m);

for i:=0 to m-1 do begin

tochka[i].X:=integer(vershina[i].x^)+round(h/(4*n));

tochka[i].Y:=integer(vershina[i].y^)+round(h/(4*n));

end;

Pen.Color:=clred;

Polygon(tochka);

brush.color:=clred;

end;

end;

DrawWay();//вызов рисования кратчайшего пути

end;

function TForm1.min(x,y:integer):integer;

begin

if x<y then result:=x else result:=y;

end;

procedure TForm1.FormResize(Sender: TObject);

var i,j:integer;

begin

h:=form1.min(Form1.ClientWidth-Panel1.Width,Form1.ClientHeight);

for i:=0 to n-1 do

for j:=0 to n-1 do begin

a[i,j].Top:=round(i*h/n);

a[i,j].Left:=round(j*h/n);

end;

Invalidate;

end;

//создание матрицы для графа

procedure TForm1.matriza();

var i,j:integer;

begin

for i:=-1 to n do

for j:=-1 to n do matr[i,j]:=False;

for i:=0 to n-1 do

for j:=0 to n-1 do begin

if a[i,j].Brush.Color=clWhite then matr[i,j]:=false

else matr[i,j]:=true;

if a[i,j].Brush.Color=clBlue then begin

nachialo.x:=i;

nachialo.y:=j;

end;

if a[i,j].Brush.Color=clYellow then begin

konez.x:=i;

konez.y:=j;

end;

end;

end;

procedure TForm1.btnGraphClick(Sender: TObject);

var i,j:integer;

begin

matriza();

wGraph.find(matr,nachialo,konez,n);

for i:=0 to n-1 do

for J:=0 to n-1 do

if a[i,j].Brush.Color=rgb(0,255,0)

then a[i,j].Brush.Color:=clGreen;

Invalidate;

end;

//процедура рисования кратчайшего пути

procedure TForm1.DrawWay;

var i,ik,jk:integer;

begin

for i:=1 to wGraph.ny do begin

ik:=wGraph.yWay[i].x;

jk:=wGraph.yWay[i].y;

a[ik,jk].Brush.Color:=RGB(0,255,0);

end;

Интерфейс(руководство пользователю)

При разработке приложения применялся принятый в среде Delphi объектно-ориентированный подход реализации интерфейса. При реализации алгоритмов обработки данных использовался структурный подход при проектировании к написании программ приложения.

Окно интерфейса приложения представлено на рисунке. Прежде всего заполняются поля размер и кол-во опорных точек.

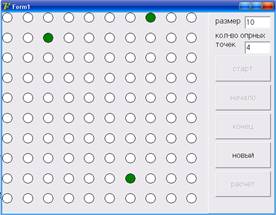
Далее по нажатию кнопки старт формируется поле Shape’ов заданной размерности. Кликами мыши выбираются опорные Shape в кол-ве заданном в поле «кол-во опорных точек».

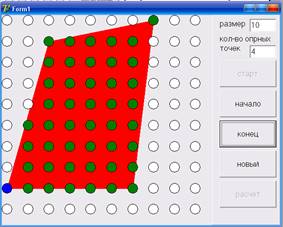
После выбора всех опорных точек отображается построенная на них область. Теперь необходимо установить начало и конец сначала нажав на соответствующую кнопку а затем на нужный Shape.Повторным нажатием на одну из этих кнопок можно изменить положение начала и конца.

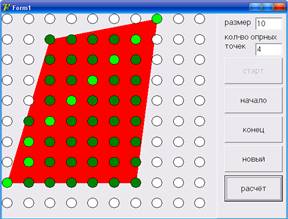
По нажатию кнопки «Расчёт» будет построен кратчайший путь, но только если между данным началом и концом он вообще существует. Для перерасчёта с изменением начала и конца следует их заново установить и нажать кнопку «Расчёт». Для изменения области нужно нажать кнопку «Новый» и приступить ко всем изложенным операциям сначала.

Тестовый пример программы

Положим размер поля равным 20 и кол-во опорных точек 10.Построим вогнутый многоугольник. Выберем начало и конец так, чтобы по прямой между ними имелись точки, не принадлежащие области.

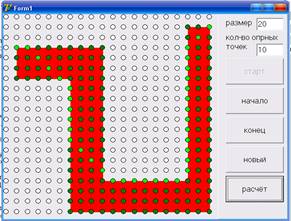
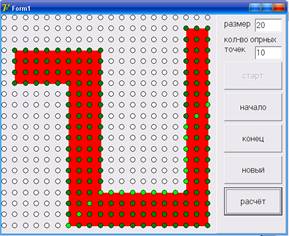
Сменим начальную и конечную точки.