Название: Рішення транспортної задачі за методом ПЗК і в Excel

Вид работы: контрольная работа

Рубрика: Информатика и программирование

Размер файла: 91.07 Kb

Скачать файл: referat.me-139676.docx

Краткое описание работы: Моделювання економики, транспортна задача, обсяги перевезень. Загальні транспортні витрати. Залежність вартості від розміру партії постачання. Ненегативність обсягів постачань. Розрахування середньої вартісті. Перевірки складеного плану перевезень.

Рішення транспортної задачі за методом ПЗК і в Excel

Рішення транспортної задачі за методом ПЗК і в Excel

Зміст

Моделювання економіки. Транспортна задача.

Список використаної літератури

Моделювання економіки. Транспортна задача

Опишемо як вирішуються транспортні задачі та наведемо приклад рішення за допомогою надбудови „Поиск решения ” у MS Excel.

Нехай існує [m] пунктів, у яких зосереджено деякий однорідний вантаж. Номер пункту зосередження [i] = 1,m. Нехай відома кільккість вантажу, що знаходиться у кожному пункті зосередження [a_i ]. Цей вантаж треба доставити до [n] пунктів споживання. Номер пункту споживання [j]=1,n. Нехай відома потреба [b_ij ] у цьому вантажі у кожному пункті споживання. Також відомі питомі витрати на перевезення вантажу з i-того пункту зосередження до j-того пункту споживання [c_ij ]. Треба визначити, скільки вантажу треба везти з кожного з пунктів зосередження до кожного з пунктів споживання таким чином, щоб з кожного пункту зосередження загалом вивозилоси не більше, ніж там є, а до кожного пункту споживання не менше від потреби (), і загальна вартість перевезень була якомога меншою.

Розв’язок :

Позначимо невідомі обсяги перевезень з кодного пункту зосередження до кожного пункту споживання [x_ij ]. Отже, умова про те, що загальна кількість вантажу, вивезена з кожного пункту зосередження, не перевищує кільксітвантажу в ньому:

Умова про те, що потреба кожного пункту споживання має задовільнятися:

Обсяги перевезень між кожним пунктом зосередження і споживання – невід’мні величчини:

Розглянуті нерівності визначають деяку множину, до якої належить багато варіантів перевезень. Серед цих варіантів треба обрати такі, що мінімізували б функцію:

(пошук умовного мінімуму для функції багатьох змінних).

Приклад

Заводи деякої автомобільної фірми розміщено у містах А, В, С та D. Основні центри розподілення продукції сконцентровано у містах 1, 2, 3 та 4. Обсяги виробництва заводів наведено у таблиці, так само як величини попиту у центрах розподілення. Вартість перевезення автомобілів залізницею по кожному із маршрутів або час перевезення по кожному із маршрутів наведено у таблиці.

Побудуйте математичну модель, яка дозволить визначити кількість автомобілів, що перевозиться з кожного заводу у кожен розподільчий центр, та оптимальний план перевезень таким чином, щоб загальні транспортні витрати були мінімальними.

Пункт	71
Місто А	1000
Місто В	1300
Місто С	1400
Місто D	800
Розподільчий центр (РЦ) у місті 1	1300
РЦ у місті 2	1500
РЦ у місті 3	500
РЦ у місті 4	1200

Пункт	Критерій оптимальності – вартість перевезення автомобілів, $/шт
	71
A-1	150
A-2	95
A-3	100
A-4	50
B-1	65
B-2	45
B-3	55
B-4	130
С-1	65
С-2	80
С-3	75
С-4	65
D-1	55
D-2	80
D-3	60
D-4	40

Для рішення задачі побудуємо її математичну модель.

Невідомими є обсяги перевезень. Нехай x_ij – обсяги перевезень з і-го постачальника до j-го продавця. Цільовою функцією є залежність вартості від розміру партії постачання:

(1),

де c_ij – вартості перевезень с i-го постачальника до j-го продавця.

Цільова функція

F = 150x₁₁ + 95x₁₂ + 100x₁₃ +50x₁₄ + 65x₂₁ +45x₂₂ +55x₂₃ +130x₂₄ +65x₃₁ + 80x₃₂ +75x₃₃ +65x₃₄ +55x₄₁ +80x₄₂ +60x₄₃ +40x₄₄ → min.

Крім цього, невідомі повинні задовольняти таким обмеженням:

- ненегативність обсягів постачань

x_ij ≥0.

- розглянемо модель типу:

,

Розмістимо дані ситуаційної задачі в спеціальній таблиці:

Покупці Постачальники	1	2	3	4	Виробництво
А	150	95	100	50	1000
B	65	45	55	130	1300
C	65	80	75	65	1400
D	55	80	60	40	800
Попит	1300	1500	500	1200

У клітинах, що стоять на перетині постачальника й покупця, ставимо довільні цифри, відстань від споживача до постачальника.

Перевіримо ситуацію на баланс:

Виробництво = 1000 + 1300 + 1400 + 800 = 4500

Попит = 1300 + 1500 + 500 + 1200 = 4500

Баланс виконується, тому не треба додавати фіктивні пункти споживання чи попиту.

Побудуємо план перевезень методом північно-західного кута:

Покупці Постачальники	а	б	в	г	Виробництво
А	1000	1000
B	300	1000	1300
C	500	500	400	1400
D	800	800
Попит	1300	1500	500	1200

Розрахуємо середню вартість, на яку перевозиться вантаж:

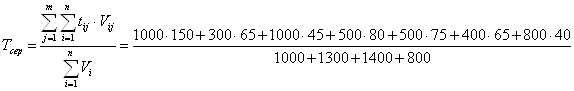
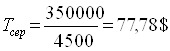
Ще раз побудуємо план:

ПокупціПостачальники	а	б	в	г	Виробництво
А	1000	1000
B	300	800	200	1300
C	200	700	300	200	1400
D	800	800
Попит	1300	1500	500	1200

Розрахуємо середню вартість:

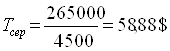
Як бачимо, другий план значно краще, вартісь перевезення вантажу скоротилася на 18,89 $.

Для перевірки оптимальності складеного плану перевезень скористаємося надбудовою „Поиск решения ” MS Excel (рис.1.1 і.1.3).

До комірки F10 внесено формулу =СУММ(B10:E10) і простягнуто її до комірки F13, до комірки В14 внесено формулу =СУММ(B10:B13) і простягнуто її до комірки Е14. До цільовій комірці G14 введено формулу (1) у вигляді виразу =СУММПРОИЗВ(B4:E7;B10:E13).

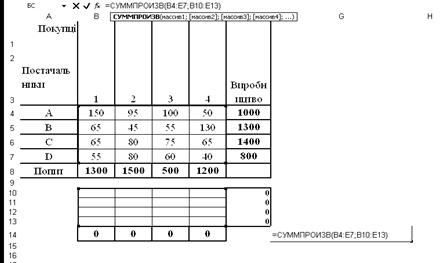
Рис.1.1.

На рис.1.2. наведено внесення обмежень моделі у діалоговому вікні надбудови „Поиск решения ”.

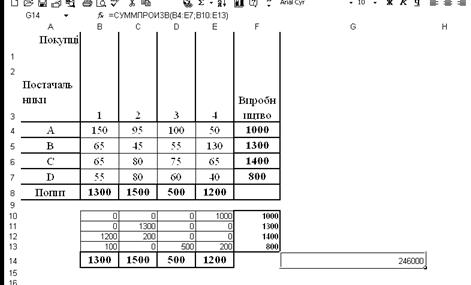
Рис.1.3.

Розрахуємо середню вартість:

Як бачимо, останній план значно краще, вартісь перевезення вантажу скоротилася на 23,11 $.

Список використаної літератури

1. Николин В.И. Автотранспортный процесс и оптимизация его элементов. - М.: Транспорт, 1990.

2. Боборыкин В.А. Математические методы решения транспортных задач. - Л.: СЗПИ, 1986.

3. Геронимус Б.А. Экономико-математические методы в планировании на автомобильном транспорте. - М.: Транспорт, 1982.

4. Аникин Б.А., Тяпухин А.П. Коммерческая логистика // Издательство Велби. М.: – 2005. – 432 с.