Название: Дослідження перехідних характеристик цифрових САК

Вид работы: лабораторная работа

Рубрика: Информатика и программирование

Размер файла: 93.21 Kb

Скачать файл: referat.me-139879.docx

Краткое описание работы: Дослідження цифрових систем автоматичного керування. Типові вхідні сигнали. Моделювання цифрової та неперервної САК із використання MatLab. Результати обчислень в програмі MatLab. Збільшення періоду дискретизації цифрової системи автоматичного керування.

Дослідження перехідних характеристик цифрових САК

Лабораторна робота №1

ДОСЛІДЖЕННЯ ПЕКРЕХІДНИХ ХАРАКТЕРИСТИК ЦИФРОВИХ САК

Мета робота: Дослідити перехідні характеристики цифрових систем автоматичного керування для типових вхідних сигналів.

Порядок виконання роботи

1. Згідно з заданим варіантом (№51)випишемо вихідні параметри досліджуваної цифрової (Ц) САК, наведеної на рис. 1.1.

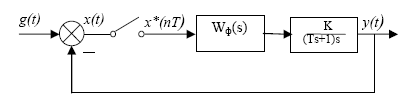
Рис. 1.1. Структурна схема досліджуваної цифрової САК

w0(s) = - неперервна дискретна САК.

2. Визначимо передатні функції розімкненої та замкненої САК відносно вхідного сигналу в загальному випадку. Для цього виконаємо z-перетворення Лапласа Z за допомогою таблиць перетворень Лапласа, виконавши наступні дії:

1) .

2) Для зручності перетворення розкладемо функцію на прості дроби

.

Маємо (4A+C)s² + (A+4B)s + B = 4, тоді s⁰ | B = 4;

s¹ | A+4B = 0, A = -16;

s² | 4A+C = 0, C = -64.

Тобто .

3) Виконаємо z-перетворення Z

4) Отримаємо передаточну функцію розімкненої САК в z-формі:

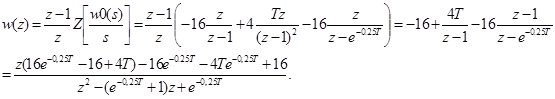
5) Передаточна функція замкнено САК:

Ф(z) = .

3. Визначимо передатні функції розімкненої та замкненої САК відносно вхідного сигналу для двох значень періоду квантування Т_к = 0,2, Т_к = 0,8:

а) при Т_к = 0,2:

1) передаточна функція розімкненої САК:

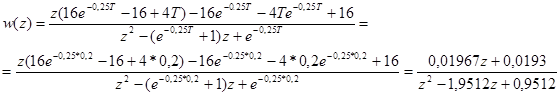
2) передаточна функція замкненої САК:

Ф(z) =

б) при Т_к = 0,8:

1) передаточна функція розімкненої САК:

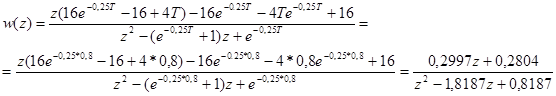
2) передаточна функція замкненої САК:

Ф(z) = .

4. Визначимо аналітично перехідні характеристики ЦСАК Y(z) = Ф(z)*G(z), де G(z) = - зображення вхідного одиничного сигналу. Тобто

а) при Т_к = 0,2 Y(z) = .

б) при Т_к = 0,8Y(z) = .

5. Побудуємо графіки перехідних процесів, попередньо розклавши перехідні характеристики в ряд Лорана:

а) при Т_к = 0,2

_

_

_

_

Тобто C₁ = 0,01967, C₂ = 0,077, C₃ = 0,1686, C₄ = 0,2839, C₅ = 0,4176. За цими даними побудуємо графік-гістограму перехідного процесу (рис. 1.2).

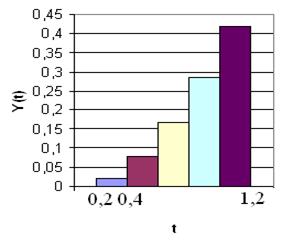
Рис. 1.2. Перехідна характеристика досліджуваної ЦСАК з періодом квантування Т_к = 0,2

б) при Т_к = 0,8

_

_

_

_

Таким чином, C₁ = 0,2997, C₂ = 1,0353, C₃ = 1,8233, C₄ = 2,2118, C₅ = 1,9358.

Побудуємо графік ЦСАК, враховуючи, що період квантування Т_к = 0,8 (рис. 1.3).

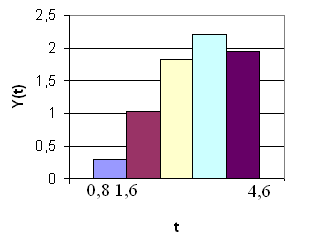
Рис. 1.3. Перехідна характеристика досліджуваної ЦСАК з періодом квантування Т_к = 0,8

6. Проведемо моделювання цифрової та неперервної САК із використання MatLab:

» k=4

k = 4

» T=4

T = 4

» w0=tf([k],[T 1 0])

Transfer function:

4

---------

4 s^2 + s

» wz1=c2d(w0,0.2)

Transfer function:

0.01967 z + 0.01935

----------------------

z^2 - 1.951 z + 0.9512

Sampling time: 0.2

» wz2=c2d(w0,0.8)

Transfer function:

0.2997 z + 0.2804

----------------------

z^2 - 1.819 z + 0.8187

Sampling time: 0.8

» Fz1=wz1/(wz1+1)

Transfer function:

0.01967 z^3 - 0.01904 z^2 - 0.01904 z + 0.0184

----------------------------------------------

z^4 - 3.883 z^3 + 5.691 z^2 - 3.731 z + 0.9232

Sampling time: 0.2

» Fz2=wz2/(wz2+1)

Transfer function:

0.2997 z^3 - 0.2647 z^2 - 0.2645 z + 0.2295

----------------------------------------------

z^4 - 3.338 z^3 + 4.681 z^2 - 3.243 z + 0.8999

Sampling time: 0.8

» Step(Fz1,60)

» Step(Fz2,60)

» F0=w0/(w0+1)

Transfer function:

16 s^2 + 4 s

-----------------------------

16 s^4 + 8 s^3 + 17 s^2 + 4 s

» Step(F0,20)

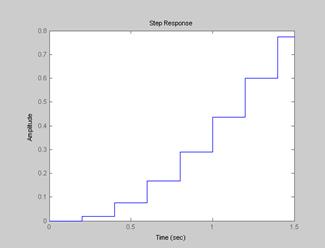
Приведемо графіки перехідних процесів, отримані за допомогою програмного пакету MatLab.

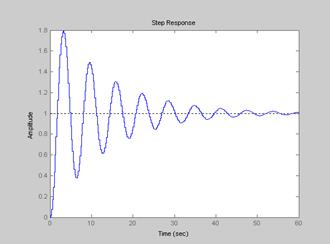
Рис. 1.4. Перехідна характеристика досліджуваної ЦСАК отримана за допомогою MatLab, період квантування Т_к = 0,2

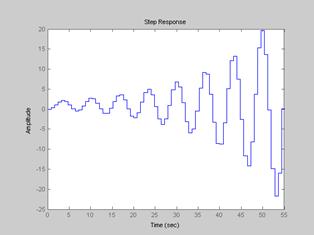
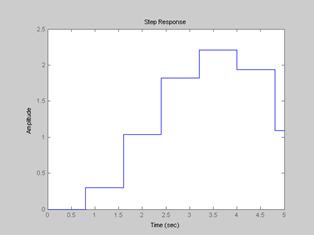
Рис. 1.5. Перехідна характеристика досліджуваної ЦСАК отримана за допомогою MatLab, період квантування Т_к = 0,8

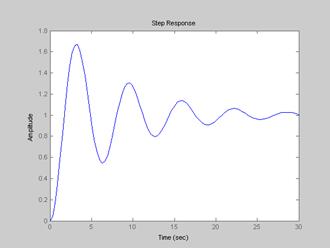
Рис. 1.6. Перехідна характеристика неперервної САК

Висновок

Виконуючи дану роботу, ми провели дослідження цифрових систем автоматичного керування. Я переконалася в правильності власних теоретичних розрахунків, порівнюючи отримані результати з результатами обчислень в програмі MatLab. Виявилося, що зі збільшенням періоду дискретизації цифрової САК правильність роботи системи страждає, тобто якість системи погіршується. Виконуючи лабораторну роботу, я також закріпила навички z-перетворення Лапласа функцій.