Referat.me
/ / Лінії передач для інтегральних схем

Название: Лінії передач для інтегральних схем

Вид работы: реферат

Рубрика: Астрономия

Размер файла: 113.1 Kb

Скачать файл: referat.me-4685.docx

Краткое описание работы: Лекція 9 . В інтегральній електроніці використовуються в основному плоскі лінії. Симетрично – смушкова лінія (ССЛ): вона відкрита, тому має втрати. Не симетрично – смушкова лінія (НСЛ):

Лінії передач для інтегральних схем

Лекція 9

Лінії передач для інтегральних схем.

В інтегральній електроніці використовуються в основному плоскі лінії.

1. Симетрично – смушкова лінія (ССЛ): вона відкрита, тому має втрати.


2. Не симетрично – смушкова лінія (НСЛ):


3. Мікросмушкова лінія (microstrip line) – МСЛ. Тут ємність дуже велика, енергія сконцентрована. Підкладка з діелектрика . Лінія двоповерхова – це не дуже зручно.


4. Щілинна лінія (slot line). Вона є одноповерховою:


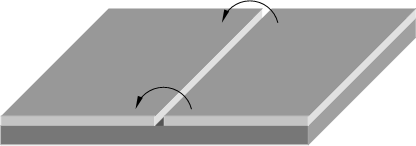5. Компланарний хвильовід – все в одній площині.


Поля в несиметрично – смушковій лінії.

Складність розв’язання цієї задачі полягає в тому, що граничні умови тут – нерегулярні; не можна покласти, що на поверхні . Використовують наближені методи; зокрема конформних відображень.


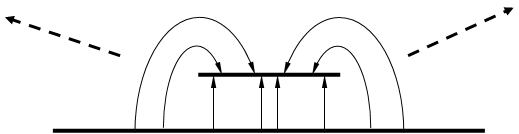
Наближення : Існує Т – хвиля (нехтуємо випромінюванням). Використаємо симетрію задачі. Цікавимося випромінюванням на краю.


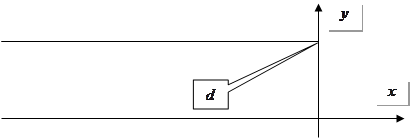Треба розв’язати задачу: знайти розв’язок рівняння Лапласа у верхній площині з напівнескінченним розрізом. Використаємо метод конформних відображень: тут застосовується інтегральне конформне перетворення Кристофеля – Шварца.


Розглянемо ламану лінію, що в точці а змінює напрямок на кут :


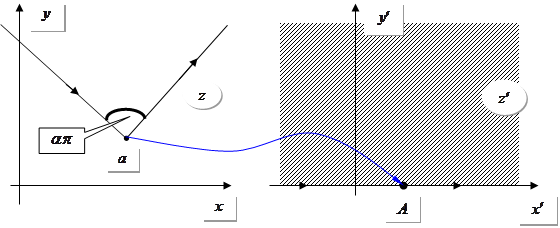. Якщо є два зломи, то , де , , . В нашій конкретній задачі ламану можна подати у вигляді:


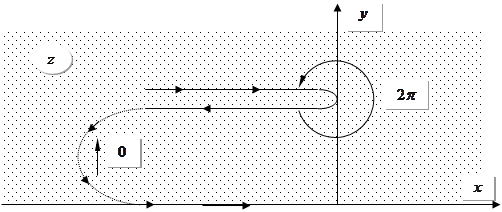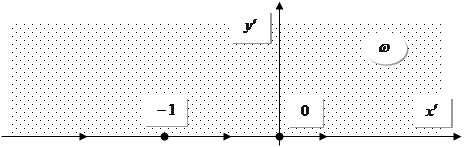Кут відраховується проти годинникової стрілки від наступного напрямку до попереднього. , , перенесемо точки: .

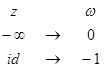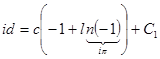Проінтегрувавши отримаємо шукане перетворення: . Константи та визначаються з умов: , отже . Умовою ми не можемо скористатися, бо одержимо . Використаємо фізичні міркування:


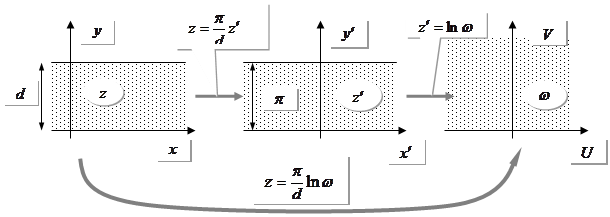
Загальний вид відображення ; бо область інваріанта відносно зсуву вздовж ОХ (трансляційна симетрія).

Зрозуміло, у нашій задачі область при . При перетворення набуває вигляду: . Порівнюючи з , . Отже шукане перетворення: .

Для того, щоб знайти розв’язок у верхній півплощині, необхідно перетворити її в конденсатор, використовуючи перетворення зворотне до : . Тоді відображення, що перетворить вихідну область () (край конденсатора) у конденсатор (), має вигляд: .

Тепер необхідно розв’язати рівняння у плоскому конденсаторі та скористатись зворотнім перетворенням: , . .


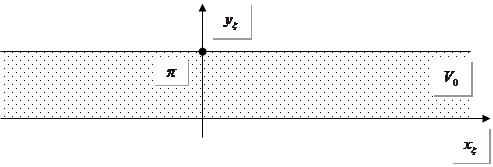
Таким чином: .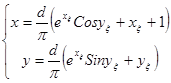

Запишемо рівняння еквіпотенційних поверхонь: .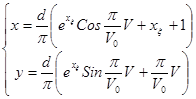

ЕПП переходить в .

ЕПП переходить в .

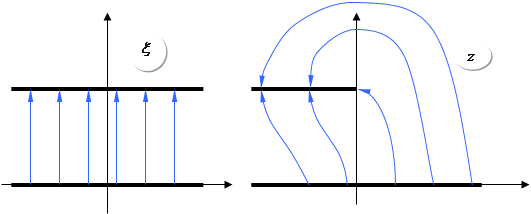
Таким чином, отримаємо таку картину еквіпотенціальних поверхонь:


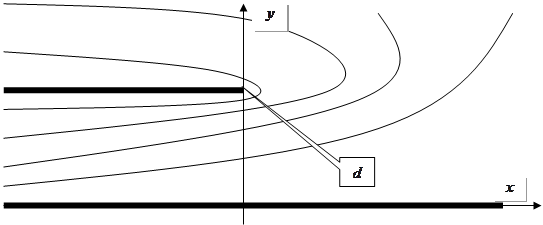
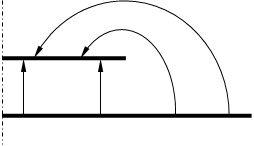
Тепер знайдемо електричні силові лінії. Ці лінії перпендикулярні ЕПП, однак ми знайдемо їх в аналітичний спосіб. Очевидно, в () такі силові лінії, як на малюнку. Знайдемо образ цих ліній у просторі (). Наприклад, 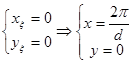,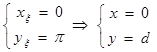. Отримаємо картину ЕП в ():


Часто важливо знайти напруженість поля в певній точці: .

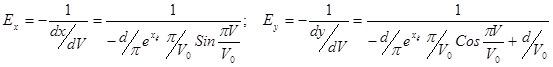
Похожие работы

  • Панель інструментів Рисование Опис усіх пунктів панелі призначення та використовування панелі

    Мета: Навчитися створювати графічні зображення за допомогою панелі інструментів “Рисование”. Хід роботи: Редактор Word має можливість створювати нескладні векторні зображення. Для реалізації цієї можливості використовується вбудований графічний редактор, який викликає за допомогою піктограми, яка знаходиться на панелі інструментів.

  • Графічні методи зображення статистичних даних

    Тема: . План Поняття про статистичні графіки і правила їх побудови. Види графіків: а) лінійні графіки; б) стовпчикові діаграми; в) секторні діаграми;

  • Відсікання відрізків

    Реферат з інформатики НА тему: Відсікання відрізків Якщо зображення виходить за межі екрані, то на частині дисплеїв збільшується час побудови за рахунок того, що зображення будується в "думці". В деяких дисплеях вихід за межі екрану призводять до спотворення картини, так як координати просто обмежуються при досягненні ними граничних значень, а не виконується точний розрахунок координат перетину (ефект "стягнення" зображення).

  • Еліпсоїд

    1) ом називається поверхня, яка в деякій прямокутній системі координат визначається рівнянням. Рівняння (1) називається канонічним рівнянням еліпсоїда. Дослідження форми еліпсоїда проведемо методом паралельних перерізів. Для цього розглянемо перерізи даного еліпсоїда площинами, паралельними площині Оху.

  • Дослідження резонаторів НВЧ

    Університет “Львівська Політехніка” ДОСЛІДЖЕННЯ РЕЗОНАТОРІВ НВЧ ВСТУП. Коливальні системи діапазону НВЧ конструктивно реалізуються у вигляді областей простору, обмеженого зі всіх сторін металевою оболонкою. Такі коли-

  • Графіка Основні теги для використання графіки у HTML документі

    Лабораторна робота№7 Тема: Графіка Мета: Опанувати технологію використання графічних зображень при оформленні HTML-документа. Теоретичні відомості.

  • Геометрична структура форми одягу Силует в одязі

    ТЕМА: ГЕОМЕТРИЧНА СТРУКТУРА ФОРМИ ОДЯГУ. СИЛУЕТ В ОДЯЗІ План 1. Визначення поняття “силует” 2. Емоційне сприйняття силуетних форм. 3. Класифікація силуетних форм.

  • Типи алгоритмів

    1. Способи запису алгоритмів. 2. Блок-схеми і правила зображення блок-схеми. 3. Типи алгоритмів. 4. Складання блок-схем. Способи запису алгоритмів.

  • Поверхні обертання Циліндричні та конічні поверхні Канонічні рівняння поверхонь другого порядку

    Пошукова робота на тему: Поверхні обертання.Циліндричні та конічні поверхні. Канонічні рівняння поверхонь другого порядку (сфера, еліпсоїд, гіперболоїди, еліптичний і гіперболічний параболоїди).

  • Застосування векторів до розв язування простих задач на площині та в просторі Рівняння та нерів

    Пошукова робота на тему: Застосування векторів до розв’язування простих задач на площині та в просторі. Рівняння та нерівності першого степеня на площині та в просторі, їх геометричний зміст. Системи рівнянь і нерівностей першого степеня.